2.Основное правило комбинаторики.

Комбинаторика-наука о конечных множествах, занимается подсчетом числа всех возможных способов расположения эл-тов конечного множ-ва. Основное правило–умнож.

n!-произведение первых n чисел натурального ряда.

Сочетания-произвольное К элементное подмножество n элементного множества наз. сочетанием из n элем-тов по k. ( )

Различные упорядоченные мн-ва, кот. отличаются лишь порядком эл-тов, т.е. полученные из того же множества наз перестанов ками ( )n-кол-во перестановок.

Упорядоточенное К элементноеное подмножество, множ-во состоящее из n эл-тов наз. размещением.

Бином Ньютона -коэф.

3. Классификация событий.

1) Случайное событие – может либо произойти, либо нет.(Об. А,В,С)

2) Достоверные события – обязательно произойдет при определенном комплексе условий.

3)Невозможное событие – событие которое никогда не произойдет

4) Несовместные события – такие события А и В, появление одного исключает появление другого.

5)Равновозможные – одно из них не является более возможным.

6)Единственно возможное событие – из нескольких событий обязательно должно произойти хотя бы одно из них(больше/равно 1)

Полную группу событий образуют несовместные и единственно возможные события (=1 и только одно событие)

Противоположные события – два несовместных события из которых 1 обязательно произойдет.

4.1 Классическое определение вероятности

Вероятность случ. соб. – это численная мера объективной возможности его наступления.

Класс.Опр.Вер.: Пусть мн-во содержит конечное число исходов и все они равновозможны.

Вероятностью случайного события (А(Р(А)), наз. число , т.е. отношение числа исходов, благоприятствующих появлению события А к числу равновозможных исходов.

Св-ва:

1)Для любого случайного события ,

2) Для достоверного события вероятность его появления =1

3) Если случайное соб. А и В несовместны(нет общих исходов, то ) Вероятность суммы этих событий =P(A)+P(B)

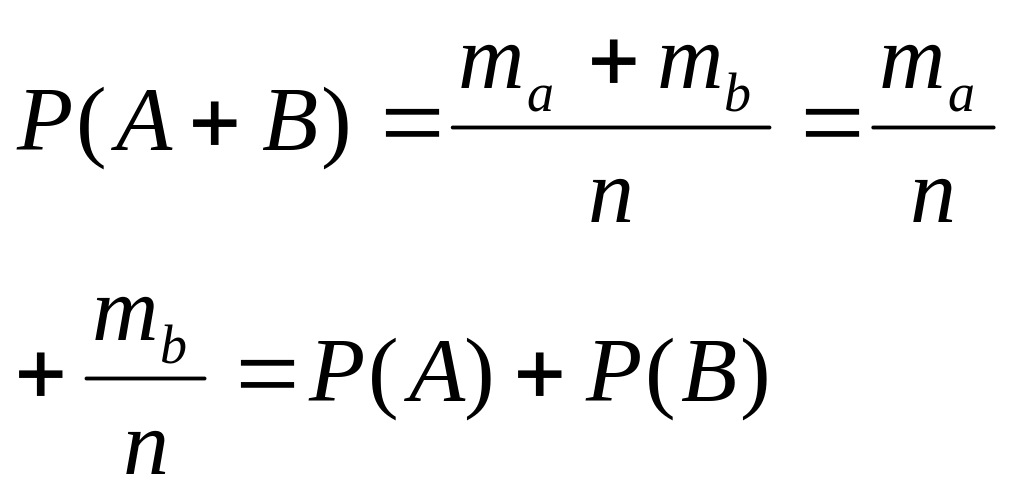
m благоприятствует А и В

Недостатки классики:

- имеет конечное число исходов

- условия равновозмож-

ностей исходов

4.2 Аксиоматическое, статистическое, геометрическое определение.

Статистическое:

Частота события А – это отношение числа опытов в которых наблюдалось событие А к общему числу опытов

; P(A)~=r(A)

В кач-ве вероятн. соб. А приним.

предел частоты соб. А при неограниченном увеличении числа опытов.

Недостатки:

- невозм. повт. опыт. беск. число раз

- заранее (до опыта) ничего нельзя сказать о вероятности события

Геометрическое:

Геометр. вероятн. соб. А наз. отношение меры области благоприятствующей появлению события А к мере всей области.

*Вероятность попадания точки на отрезок l определяется равенством: P=Длина l/Длина L. *Вероятность попадания точки в фигуру g определяется равенством: P=площадь g/площадь G.

Аксиоматическое:

Полем событий(W( )) наз. совокупность таких подмножеств , удовлетворяющих след. условиям:

1)

2) А и В произвольные эл-ты из W( ) , Вероятность произвольного события А принадл. W( ) наз. любая функция P(A) со значениями в множестве действительных чисел R и удовл. 3-м аксиомам:

-

-

- если АВ= , то

Действия над событиями. Венн.

При общем определении вероятности используется пространство элементарных событий, при этом элементарные события являются неопределяемым понятием, но относительно них предполагается, что в результате испытаний обязательно происходит одно из этих элементарных событий. Элементарные события попарно не совместны и образуют группу событий. События, не являющиеся элементарными, отождествляются с теми элементарными событиями, которые благоприятствуют ему, следовательно, случайные события можно рассматривать как подмножество в пространстве элементарных событий, поэтому операции над случайными событиями: объединение (сложение), пересечение (умножение), эквивалентность, отрицание – полностью совпадают с соответствующими операциями над множествами. Операции объединения и пересечения множеств симметричны, т.е.

A B = B A A B = B A

Диаграмма Венна