
- •Матрицы: основные понятия, алгебраические операции и их св-ва, ранг матрицы, элементарные преобразования.
- •Определители второго и третьего, n-го порядка, св-ва определителей, вычисление обратной матрицы.
- •Свойства определителей:
- •Вычисление обратной матрицы.
- •Системы линейных уравнений: основные понятия, методы решения: матричный, Крамера, Гаусса.
- •Методы решения:
- •10. Метод Гаусса решения слу:
- •Основные понятия:
- •Произведения векторов:
- •Прямая на плоскости: основные уравнения, взаимное расположение двух прямых. Формулы расстояния от точки до прямой, длины отрезка.
- •Кривые второго порядка: эллипс, гипербола, парабола: определение, канонические уравнения, свойства, способ построения.
- •Кривые второго порядка:
- •Эллипс, гипербола, парабола, окружность:
- •Полярная система координат.
- •Пределы: основные понятия и их свойства.
- •Бесконечно большие и бесконечно малые функции, сравнение бесконечно малых, связь между бесконечно малыми и бесконечно большими функциями.
- •Замечательные пределы.
- •Первый замечательный предел
- •Эквивалентные бесконечно малые функции, основные эквивалентности.
- •Непрерывность функции, классификация точек разрыва. Св-ва функций, непрерывных на отрезке.
- •Асимптоты графика функций.
- •Приложение производной для раскрытия неопределенностей в пределах.
- •Формула Тейлора. Разложение в ряд функций.
- •Ф ункции нескольких переменных (фнп): определение, св-ва, график, линии и поверхности уровня.
- •Предел и непрерывность фнп. Дифференцируемость фнп.
- •1.1.2 Предел функции в точке
- •1.1.3 Непрерывность функции двух переменных в точке
- •1.1.5 Дифференцируемость функции двух переменных, дифференциал
- •Классификация областей.
- •Производная и дифференциал фнп: частные производные, геометрический смысл (уравнение нормали и касательной плоскости).
- •Производная сложной и неявной функции, полная производная.
- •Частные производные и дифференциал высших порядков фнп.
- •Экстремум функции нескольких переменных.
- •Скалярное поле: производная по направлению, градиент, связь между ними; физический смысл, св-ва градиента.
Кривые второго порядка: эллипс, гипербола, парабола: определение, канонические уравнения, свойства, способ построения.
Кривые второго порядка:
Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида
![]()
в
котором по крайней мере один из
коэффициентов ![]() отличен
от нуля.
отличен
от нуля.
Невырожденные кривые
Кривая
второго порядка называется невырожденной,
если ![]() Могут
возникать следующие варианты:
Могут
возникать следующие варианты:
Невырожденная кривая второго порядка называется центральной, если
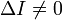
эллипс — при условии D > 0 и ΔI < 0;
частный случай эллипса — окружность — при условии I2 = 4D или a11 = a22,a12 = 0;
мнимый эллипс (ни одной вещественной точки) — при условии ΔI > 0;
гипербола — при условии D < 0;
Невырожденная кривая второго порядка называется нецентральной, если ΔI = 0
парабола — при условии D = 0.
Вырожденные кривые
Кривая второго порядка называется вырожденной, если Δ = 0. Могут возникать следующие варианты:
вещественная точка на пересечении двух мнимых прямых (вырожденный эллипс) — при условии D > 0;
пара вещественных пересекающихся прямых (вырожденная гипербола) — при условии D < 0;
вырожденная парабола — при условии D = 0:
пара вещественных параллельных прямых — при условии B < 0;
одна вещественная прямая (две слившиеся параллельные прямые) — при условии B = 0;
пара мнимых параллельных прямых (ни одной вещественной точки) — при условии B > 0.
Эллипс, гипербола, парабола, окружность:
Окружность: (x-x0)2 + (y-y0)2 = R2,
Парабола: y-y0 = 2p(x-x0)2или x-x0=2p(y-y0)2,
Эллипс – множество точек плоскости, сумма расстояния от которых до двух данных (называемая фокусами) есть величина постоянная, больше, чем расстояние между этими точками.| F1M | + | F2M | = const, const>|F1F2|, |F1F2| - фокусное расстояние.
![]() - уравнение эллипса
в центре начала координат. |a|
- длина большой полуоси, в2
= а2
– с2,
|в| - длина малой полуоси.
- уравнение эллипса
в центре начала координат. |a|
- длина большой полуоси, в2
= а2
– с2,
|в| - длина малой полуоси.![]() ,
где x0и y0
– координаты центра эллипса.
,
где x0и y0
– координаты центра эллипса.
Гипербола – множество точек плоскости, модуль разности от каждых из которых до двух заданных (фокусами) есть величина постоянная, меньше чем расстояние между фокусами.
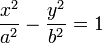 ,
|а|
- длина действительной полуоси,в2
= с2
– а2,
|в| - длина мнимой полуоси.
,
|а|
- длина действительной полуоси,в2
= с2
– а2,
|в| - длина мнимой полуоси.
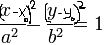
Полярная система координат.


Формулы перехода от декартовой системы координат к полярной и обратно
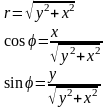
x=r cos
y=r sin
Обратная связь:
Пусть известны x и y:
Полярные уравнения кривых второго порядка
Выберем начало отсчета (полюс) в одном из фокусов. (F1=0)
Для
любых точек М
эллипсу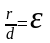 (*)
(*)
Так как для эллипса фиксировано расстояние от фокуса до директрисы, то вводим обозначение для этого расстояния - р.
Тогда расстояние от точки М до директрисы в полярной системе примет вид:
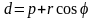
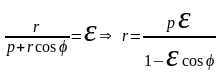 (1)
– полярноеур эллипса (
1)
(1)
– полярноеур эллипса (
1)
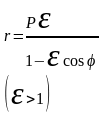 (2)-
полярное уравнение гиперболы.
(2)-
полярное уравнение гиперболы.
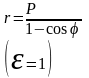 Полярное
уравнение параболы: (3)
Полярное
уравнение параболы: (3)
Предел и непрерывность
