6) Изменение матрицы линейного преобразования при изменении базиса

В предыдущем разделе мы установили, что как только в линейном пространстве выбран базис, то каждому линейному преобразованию соответствует матрица этого преобразования. Однако если выбрать в пространстве другой базис, то матрица преобразования, как правило, станет другой. Выясним, как эти матрицы связаны между собой.

Пусть    --   -мерное линейное пространство,   и    -- два базиса в этом пространстве. Первый из них назовем "старым", а второй -- "новым". Пусть    -- матрица перехода 19.1.4 а от старого базиса к новому.

        Предложение 19.1   Пусть    -- линейное преобразование пространства   ,   и    -- матрицы этого преобразования в старом и новом базисе соответственно. Тогда

        Доказательство.     Пусть    -- произвольный вектор пространства   ,    -- его образ, то есть   . Пусть   и    -- координатные столбцы векторов   и   в старом базисе, а   ,    -- в новом. Тогда в силу формулы (19.3)   . По  предложению 18.5 имеем   ,   . Подставим эти выражения в предыдущую формулу, получаем   . Откуда   . С другой стороны, в силу формулы (19.3) в новом базисе   . Сравнивая это равенство с предыдущим, получаем   .      

        Определение 19.2   Две квадратных матрицы   и   одного порядка называются подобными, если существует такая невырожденная матрица   , что   .         

        Следствие 19.1   Матрицы одного линейного преобразования, соответствующие разным базисам, подобны друг другу, и наоборот, если матрицы подобны, то они являются матрицами одного и того же преобразования в разных базисах.

Определение и примеры

Рассмотрим линейное пространство   и преобразование   этого пространства, то есть закон, по которому каждому вектору   из  соответствует вектор   из того же пространства. Вектор   называется образом вектора   и обозначается   , а вектор   называетсяпрообразом вектора   .

        Определение 19.1   Преобразование   линейного пространства   называется линейным, если для любых векторов   и   и любого числа   выполнены равенства

(19.1)

то есть образ суммы векторов равен сумме образов слагаемых, образ вектора, умноженного на число, равен произведению этого числа на образ вектора.         

        Замечание 19.1   В этой главе с каждым линейным преобразованием будет связана матрица, которую мы будем обозначать той же буквой, что и само преобразование. Чтобы их различать, мы для букв, обозначающих преобразование, будем использовать так называемый "каллиграфический" шрифт.         

Линейное преобразование пространства   называют также линейным отображением из   в   или линейным оператором из   в   .

Исходя из равенств (19.1) легко проверить, что

то есть образ линейной комбинации векторов равен линейной комбинации их образов.

Рассмотрим несколько примеров линейных преобразований.

        Пример 19.1   Пусть    -- двумерное векторное пространство, то есть множество векторов плоскости. Пусть   . Это преобразование действует так: каждый вектор оно переводит в вектор такого же направления, но в два раза большей длины. Если считать, что все векторы имеют начало в начале координат, то преобразование   можно представить как растяжение плоскости в два раза (рис. 19.1).

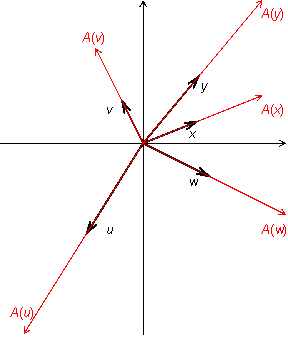
Рис.19.1.Преобразование растяжения

Проверим выполнение равенств (19.1)

Равенства (19.1) выполнены, следовательно, преобразование   является линейным.         

        Пример 19.2   Пусть    -- двумерное векторное пространство,    -- поворот вектора по часовой стрелке на угол   (рис. 19.2).

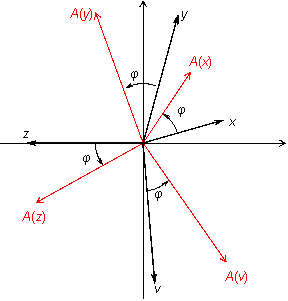
Рис.19.2.Преобразование поворота

Покажем, что это -- линейное преобразование.

Пусть   и    -- два вектора. Тогда    -- это диагональ параллелограмма со стронами   ,   (рис. 19.3).

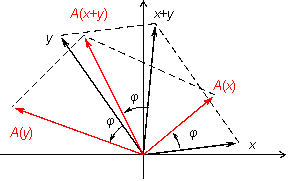
Рис.19.3.Образ суммы векторов

Если параллелограмм повернуть как единое целое на угол   , то его стороны станут векторами   и   , диагональ будет вектором   . С другой стороны, диагональ тоже повернулась на угол   и поэтому является вектором   . Следовательно,   , первое из условий (19.1) выполнено.

Пусть   -- число. Из рисунка 19.4 очевидно, что   .

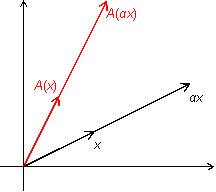
Рис.19.4.Образ вектора, умноженного на число

Следовательно, преобразование    -- линейное.         

Упражнение19.1.1. Пусть    -- двумерное векторное пространство,    -- некоторая прямая, проходящая через начало координат,    -- преобразование, переводящее каждый вектор   в вектор   симметричный исходному относительно прямой   (рис. 19.5). Другими словами,  является зеркальным отражением вектора   в прямой   .

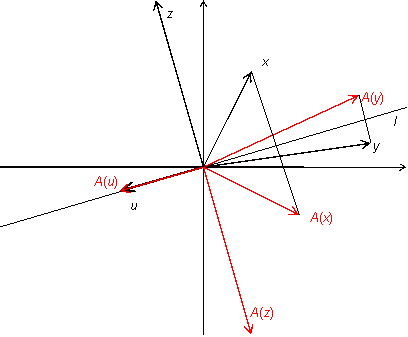
Рис.19.5.Преобразование отражения

Докажите, что   является линейным преобразованием.

Упражнение19.1.2. Пусть    -- двумерное векторное пространство,    -- некоторая прямая, проходящая через начало координат,    -- преобразование, переводящее каждый вектор   в его проекцию на прямую   (рис. 19.6).

Рис.19.6.Преобразование проектирования

Докажите, что   является линейным преобразованием.

        Пример 19.3   Пусть    -- пространство всех многочленов,    -- преобразование, которое переводит вектор из   , то есть многочлен, в производную этого многочлена, которая естественно является многочленом, то есть вектором из   . Пусть   , то есть   . Тогда

Например, если   , то   . Покажем, что преобразование   является линейным.

Пусть   ,    -- число. Тогда в силу свойства линейности производной получим

Аналогично,

Следовательно,    -- линейное преобразование.         

        Пример 19.4   Пусть    --   -мерное линейное пространство, Выберем в этом пространстве базис   . Тогда у любого вектора  есть его координатный столбец 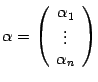  . Пусть    -- квадратная матрица порядка   . Определим преобразование   следующим образом:   является вектором, координатный столбец которого равен   (справа стоит произведение матрицы   на столбец  ). Покажем, что преобразование    -- линейное.

Пусть   и   имеют координатные столбцы   и   соответственно, а их образы   и    -- координатные столбцы   , и   . Тогда

Но выражение в последнем равенстве справа является координатным столбцом образа суммы векторов   . Следовательно,   .

Пусть    -- произвольное число. Тогда координатный столбец вектора   равен   , координатный столбец образа вектора

то есть равен числу   , умноженному на координатный столбец образа вектора   . Поэтому   . Тем самым мы доказали, что преобразование   является линейным.         

Очевидно, что примерами линейных преобразований могут служить тождественное преобразование, то есть преобразование, переводящее каждый вектор в себя,   , и нулевое преобразование, переводящее каждый вектор в нуль,   .

Легко проверяется, что для любого линейного преобразования   образ нуля равен нулю,   . Действительно, в силу второго из равенств (19.1)

8) геометрический смысл определителя

Рассмотрим систему двух линейных уравнений с двумя неизвестными. a1x + b1y = c1 a2x + b2y = c2 (1) и покажем, как решение этой системы приводит к определителю второго порядка. Сначала преобразуем систему так, чтобы каждое уравнение содержало лишь одно неизвестное. Для этого мы умножим обе части первного уравнения на b2, а второго на -b1 и сложим полученные уравнения. Тогда a1x + b1y = c1 (2) Затем умножим обе части первого уравнения на -a2, второго на а1, сложим найденные уравнения и получим (a1b2 - a2b1)y = a1c2 - a2c1 (3) При исследовании системы (1) интерес представляет тот случай, когда хотя бы один из коэффициентов a1, a2, b1, b2 не равен нулю. Будем считать, что a1 0. Рассмотрим три cлучая: a1b2 - a2b1№ 0 a1b2 - a2b1 = 0 c1b2 - c2b1 = 0. a1b2 - a2b1 = 0 c1b2 - c2b1 № 0 a1c2 - a2c1 № 0. Случай 1: Если a1b2 - a2b1 0, то из уравнений (2), (3) находим: , (4) Подставляя в уравнения системы (1) вместо x, y их значения по формулам (4), убеждаемся, что формулы (4) дают решение системы (1). Пусть х = , y =  - решение системы (1), т.е. a1 + b1 = c1 a2 + b2 = c2 Из последних равенств получим, как и выше, что (a1b2 - a2b1) = c1b2 - c2b1 (a1b2 - a2b1) = a1c2 - a2c1 Мы показали, что всякое решение системы (1) является решением системы, состоящей из уравнений (2), (3), имеет, очевидно, единственное решение, то отсюда следует, что решение системы (1), которое дают формулы (4), является единственным. Таким обрaзом, если a1b2 - a2b1 0, то система (1) имеет единственное решение. Геометрически случай 1 означает: две прямые, уравнения которых образуют систему (1), пересекаются в одной точке, абцисса и ордината которой составляют решение этой системы. Случай 2: Пусть a1b2 - a2b1 = 0 и одно из чисел c1b2 - c2b1, a1c2 - a2c1 , например первое, равно нулю; тогда равно нулю и второе число. Действительно, так как , a10, то из a1b2 - a2b1 = 0 следует = ; из 1b2 - c2b1=0 следует = ; Отсюда = = =  (5) и = ; или a1c2 - a2c1 = 0. Из равенств (5) получим: a2 = a1; b2 = b1; c2 = c1 Обе части уравнения (1) системы умножим на , тогда a1x + b1y = c1 или a2x + b2y = c2 Таким образом, второе уравнение системы (1) получится из первого умножением обеих частей первого на одно и то же число. Второе уравнение системы (1) можно отбросить. Очевидно, в этом случае система (1) имеет бесконечное множество решений. Геометрическое истолкование случая 2: обе прямые, уравнения которых образуют систему (1), совпадают. Случай 3: Пусть теперь a1b2 - a2b1 = 0, c1b2 - c2b1  0, a1c2 - a2c1 0. Тогда =  Обозначим =  тогда и =  Отсюда a2 = a1; b2 = b1 Умножив обе части первого уравнения системы (1) на , найдем a1x + b1y = c1 или a2x + b2y = c1 Левые части полученного уравнения и второго уравнения системы (1) равны, а правые - различны. Действительно, если бы c1 = c2 , то , что противоречило бы условию. Следовательно, в данном случае система не имеет решений. Геометрический смысл случая 3: прямые, уравнения котрых образут систему(1), параллельны.

9)ортогональные матрицы

Ортогональная матрица

Ортогональная матрица — квадратная матрица A с вещественными элементами, результат умножения которой на A^T равен единичной матрице:^[1]

AA^T = A^TA = E,

или, что эквивалентно, её обратная матрица равна транспонированной матрице:

Свойства

• Столбцы и строки ортогональной матрицы образуют системы ортонормированных векторов, то есть:

и

где , n — порядок матрицы, а δ_jk — символ Кронекера.

Другими словами, скалярное произведение строки на саму себя равно 1, а на любую другую строку — 0. Так же и для столбцов.

• Определитель ортогональной матрицы равен 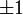, что следует из свойств определителей:

• Множество ортогональных матриц порядка n над полем k образует группу по умножению, так называемую ортогональную группу которая обозначается O_n(k) или 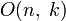(если k опускается, то предполагается ).

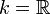• Ортогональные матрицы соответствуют линейным операторам, переводящим ортонормированный базис линейного пространства в ортонормированный.

• Любая вещественная ортогональная матрица подобна блочно-диагональной матрице с блоками вида

и

Примеры

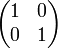• — единичная матрица

• 

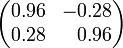• — пример матрицы поворота

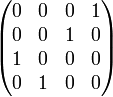• — пример перестановочной матрицы

Подобная матрица

Квадратные матрицы A и B одинакового порядка называются подобными, если существует невырожденная матрица P того же порядка, такая что:

Подобные матрицы получаются при задании одного и того же линейного преобразования матрицей в разных координатных системах; при этом матрица Р является матрицей перехода от одной системы к другой.

Если две матрицы подобны, то говорят, что одна из матриц может быть получена преобразованием подобия из другой. Если при этом одна из матриц диагональная, то про вторую матрицу говорят, что она может быть диагонализована.