
- •Для любого .
- •Базис. Размерность
- •[Править]Важные частные случаи
- •[Править]Связанные понятия
- •[Править]Примеры
- •6) Изменение матрицы линейного преобразования при изменении базиса
- •Определение и примеры
- •[Править]Свойства
- •[Править]Канонические формы подобных матриц
- •Свойства пределов функции
- •[Править]Обозначения
- •[Править]Примеры
- •[Править]Свойства
Линейное,
или векторное пространство
![]() над
полем
P — это непустое
множество L, на котором
введены операции
над
полем
P — это непустое
множество L, на котором
введены операции
сложения, то есть каждой паре элементов множества
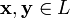 ставится
в соответствие элемент того же множества,
обозначаемый
ставится
в соответствие элемент того же множества,
обозначаемый
 и
иумножения на скаляр (то есть элемент поля P), то есть любому элементу
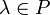 и
любому элементу
и
любому элементу
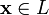 ставится
в соответствие единственный элемент
из
,
обозначаемый
ставится
в соответствие единственный элемент
из
,
обозначаемый
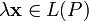 .
.
При этом на операции накладываются следующие условия:
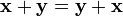 ,
для любых
(коммутативность
сложения);
,
для любых
(коммутативность
сложения);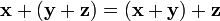 ,
для любых
,
для любых
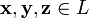 (ассоциативность
сложения);
(ассоциативность
сложения);существует такой элемент
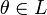 ,
что
,
что
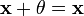 для
любого
(существование
нейтрального элемента относительно
сложения), в частности L не пусто;
для
любого
(существование
нейтрального элемента относительно
сложения), в частности L не пусто;для любого существует такой элемент
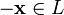 ,
что
,
что
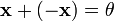 (существование
противоположного элемента относительно
сложения).
(существование
противоположного элемента относительно
сложения).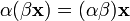 (ассоциативность
умножения на скаляр);
(ассоциативность
умножения на скаляр);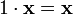 (унитарность:
умножение на нейтральный (по умножению)
элемент поля P сохраняет вектор).
(унитарность:
умножение на нейтральный (по умножению)
элемент поля P сохраняет вектор).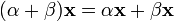 (дистрибутивность
умножения на вектор относительно
сложения скаляров);
(дистрибутивность
умножения на вектор относительно
сложения скаляров); (дистрибутивность
умножения на скаляр относительно
сложения векторов).
(дистрибутивность
умножения на скаляр относительно
сложения векторов).
Элементы множества L называют векторами, а элементы поля P — скалярами. Свойства 1-4 совпадают с аксиомами абелевой группы.
Простейшие свойства
Векторное пространство является абелевой группой по сложению.
Нейтральный элемент является единственным, что вытекает из групповых свойств.
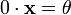 для
любого
.
для
любого
.Для любого противоположный элемент является единственным, что вытекает из групповых свойств.
 для
любого
.
для
любого
.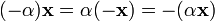 для
любых
для
любых
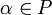 и
.
и
.Для любого .
Связанные определения и свойства
Подпространство
Алгебраическое определение: Линейное подпространство или векторное подпространство ― непустое подмножество K линейного пространства L такое, что K само является линейным пространством по отношению к определенным в L действиям сложения и умножения на скаляр. Множество всех подпространств обычно обозначают как Lat(L). Чтобы подмножество было подпространством, необходимо и достаточно, чтобы
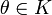 ;
;для всякого вектора
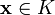 ,
вектор
,
вектор
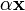 также
принадлежал K, при любом
;
также
принадлежал K, при любом
;для всяких векторов
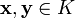 ,
вектор
,
вектор
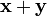 также
принадлежал K.
также
принадлежал K.
Последние два утверждения эквивалентны следующему:
для всяких векторов , вектор
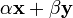 также
принадлежал K для любых
также
принадлежал K для любых
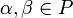 .
.
В частности, пространство, состоящее из одного элемента {θ}, является подпространством любого пространства; любое пространство является само себе подпространством. Подпространства, не совпадающие с этими двумя, называют собственными или нетривиальными.
Свойства подпространств
Пересечение любого семейства подпространств — снова подпространство;
Сумма конечного семейства подпространств — снова подпространство. Сумма подпространств
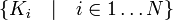 определяется
как множество, содержащее всевозможные
суммы элементов Ki:
определяется
как множество, содержащее всевозможные
суммы элементов Ki:
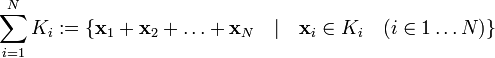 .
.
В функциональном анализе в бесконечномерных пространствах особо выделяют замкнутые подпространства.
Базис. Размерность
Конечная сумма вида
![]()
называется
линейной комбинацией элементов
![]() с
коэффициентами
с
коэффициентами
![]() .
.
Линейная комбинация называется нетривиальной, если хотя бы один из её коэффициентов отличен от нуля.
Элементы
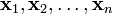 называются
линейно зависимыми, если существует
их нетривиальная линейная комбинация,
равная нулевому элементу θ. В противном
случае эти элементы называются линейно
независимыми.
называются
линейно зависимыми, если существует
их нетривиальная линейная комбинация,
равная нулевому элементу θ. В противном
случае эти элементы называются линейно
независимыми.Бесконечное подмножество векторов из L называется линейно зависимым, если линейно зависимо его некоторое конечное подмножество, и линейно независимым, если любое его конечное подмножество линейно независимо.
Число элементов (мощность) максимального линейно независимого подмножества пространства не зависит от выбора этого подмножества и называется рангом, или размерностью, пространства, а само это подмножество — базисом (базисом Га́меля или линейным базисом). Элементы базиса также называют базисными векторами. Свойства базиса:
Любые n линейно независимых элементов n-мерного пространства образуют базис этого пространства.
Любой вектор можно представить (единственным образом) в виде конечной линейной комбинации базисных элементов:
![]() .
.
Линейная оболочка
Линейная
оболочка
![]() подмножества
X линейного пространства L —
пересечение всех подпространств L,
содержащих X.
подмножества
X линейного пространства L —
пересечение всех подпространств L,
содержащих X.
Линейная оболочка является подпространством L.
Линейная оболочка также называется подпространством, порожденным X. Говорят также, что линейная оболочка натянута на множество X.
Линейная оболочка состоит из всевозможных линейных комбинаций различных конечных подсистем элементов из X. В частности, если X — конечное множество, то состоит из всех линейных комбинаций элементов X.
Если X — линейно независимое множество, то оно является базисом и тем самым определяет его размерность.
[править] Примеры
Нулевое пространство, единственным элементом которого является ноль.
Пространство всех функций
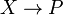 с
конечным носителем образует векторное
пространство размерности равной
мощности
X.
с
конечным носителем образует векторное
пространство размерности равной
мощности
X.поле вещественных чисел может быть рассмотрено как континуально-мерное векторное пространство над полем рациональных чисел.
Любое поле является одномерным пространством над собой.
Дополнительные структуры
Нормированное векторное пространство
Метрическое векторное пространство
Топологическое векторное пространство
Евклидово пространство
Гильбертово пространство
Матрица линейного отображения
Определение
Определение
1. Пусть
![]() и
и
![]() —
конечномерные
векторные
пространства над полем
—
конечномерные
векторные
пространства над полем
![]() с
базисами
с
базисами
![]() и
и
![]() соответственно.
Рассмотрим линейное
отображение
соответственно.
Рассмотрим линейное
отображение
![]() .
Тогда
.
Тогда
![]() можно
представить в виде
можно
представить в виде
![]() для
некоторых
для
некоторых
![]() .
Матрица
.
Матрица
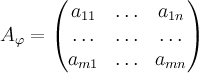 называется
матрицей линейного отображения1)
в
базисах
и
.
Столбцами этой матрицы являются
координаты векторов
в
базисе
.
называется
матрицей линейного отображения1)
в
базисах
и
.
Столбцами этой матрицы являются
координаты векторов
в
базисе
.
Пусть
произвольный вектор
![]() имеет
следующие координаты в разложении по
базису
,
имеет
следующие координаты в разложении по
базису
,
![]() ,
тогда его образ
,
тогда его образ
![]() из
пространства
в
базисе
имеет
разложение
из
пространства
в
базисе
имеет
разложение
![]() ,
где
,
где
![]() .
То есть
.
То есть
 .
.
Предложение
1. Существует взаимно
однозначное отображение
между множеством всех линейных отображений
из
![]() -мерного
векторного пространства
в
-мерного
векторного пространства
в
![]() -мерное
векторное пространство
с
фиксированными базисами и множеством
матриц размера
-мерное
векторное пространство
с
фиксированными базисами и множеством
матриц размера
![]() .
.
Определение
2. Матрица линейного оператора2)
— это матрица линейного отображения в
случае, когда
![]() .
.
Пример
1. Пусть
—
базис
-мерного
векторного пространства
![]() .
Рассмотрим тождественный3)
линейный оператор
.
Рассмотрим тождественный3)
линейный оператор
![]() .
Так как
.
Так как
![]() ,
то матрица
,
то матрица
![]() —
это в точности единичная
матрица
—
это в точности единичная
матрица
 .
.
Предложение
2. Пусть
![]() —
конечномерные векторные пространства,
—
конечномерные векторные пространства,
![]() и
и
![]() —
линейные отображения. Тогда
—
линейные отображения. Тогда
![]() .
.
Умножением
двух линейных операторов
![]() и
и
![]() на
пространстве
будем
считать их композицию:
на
пространстве
будем
считать их композицию:
![]() .
Тогда справедливо
.
Тогда справедливо
Предложение
3. Пространство линейных операторов
![]() является
ассоциативной
алгеброй
над полем
.
В случае, если пространство
конечномерно,
алгебра
изоморфна
алгебре всех матриц порядка
над
полем
.
Изоморфизм задается отображением
является
ассоциативной
алгеброй
над полем
.
В случае, если пространство
конечномерно,
алгебра
изоморфна
алгебре всех матриц порядка
над
полем
.
Изоморфизм задается отображением
![]() .
.
4) Лине́йное отображе́ние, лине́йный опера́тор — обобщение линейной числовой функции (точнее, функции y = kx) на случай более общего множества аргументов и значений. Линейные операторы, в отличие от нелинейных, достаточно хорошо исследованы, что позволяет успешно применять результаты общей теории, так как их свойства не зависят от природы величин.
Лине́йным отображе́нием векторного пространства LK над полем K в векторное пространство MK (лине́йным опера́тором из LK вMK) над тем же полем K называется отображение
![]() ,
,
удовлетворяющее условию линейности
f(x + y) = f(x) + f(y),
f(αx) = αf(x).
для
всех ![]() и
и ![]() .
.
Если определить операции сложения и умножения на скаляр из основного поля K как
множество
всех линейных отображений
из LK в MK превращается
в векторное пространство, которое обычно
обозначается как ![]()
