Вопрос 38: Оптимальное использование производственных мощностей электростанций в энергетической системе

Общие принципы оптимального использования производственных мощностей электростанции в энергетической системе (подход и методика) аналогичны распределению нагрузки внутри станции. Для определения наивыгоднейшего распределения электрической нагрузки между станциями энергосистемы или между системами в объединении систем необходимо учитывать поправочные коэффициенты на изменение потерь мощности в электрической сети:

δ =1/(1-σ) ,

где σ - относительный прирост потерь активной мощности в сети для данной станции (при распределении нагрузки между станциями системы) или для данной системы (при распределении нагрузки между энергосистемами в объединении систем). В общем случае относительный прирост потерь мощности для каждой i-й электростанции можно представить в виде

σ = ΔP/dPi =β1Р1+β2Р2+...+βiРi+...+βпРп+А,

где Р₁, Р₂, ..., Р_i, ..., Р_n --- электрические нагрузки 1, 2, ..., i, ..., п-й электростанции;  Р --- суммарные потери активной мощности; β₁, β₂, ..., β_i, ..., β_n --- постоянные коэффициенты; А --- величина, зависящая от нагрузок потребителей.  Аналогичное выражение может быть записано и при распределении нагрузок между системами. Следовательно, в общем случае относительный прирост потерь мощности данной электростанции (системы) зависит не только от нагрузки этой станции (системы), но и от нагрузок других станций (систем), параметров электрической сети, нагрузок потребителей. Изменение величины относительного прироста потерь активной мощности данной электростанции (системы) в зависимости от ее нагрузки при прочих постоянных условиях представляет характеристику относительного прироста потерь мощности. Рассмотрим характеристику относительного прироста потерь мощности на примере линии электропередачи 110 кВ, от которой питаются тяговые подстанции железнодорожного транспорта (рис. 9.18).  Эта характеристика имеет вид линии, пересекающей ось абсцисс в точке, соответствующей минимуму кривой потерь мощности ΔP = f (Р1). При увеличении активной нагрузки тяговых подстанций на транзитной линии прямая σ смещается параллельно самой себе вправо, а при увеличении напряжения на конце линии U2 - влево.  Оптимальность использования производственных мощностей энергообъединений сложной структуры, включающих электростанции различных типов с различающимися составом оборудования и видами используемых энергоресурсов, достигается при применении экономико-математических методов и ЭВМ. К ним, например, относятся: тепловые нагрузки ТЭЦ, расходы воды на ГЭС и требования неэнергетических водопользователей, ограничения по режиму использования АЭС, параметры и схемы электрических сетей, характеристики топливоснабжения и условия использования нетранспортабельных видов топлива, вторичных энергоресурсов и др.

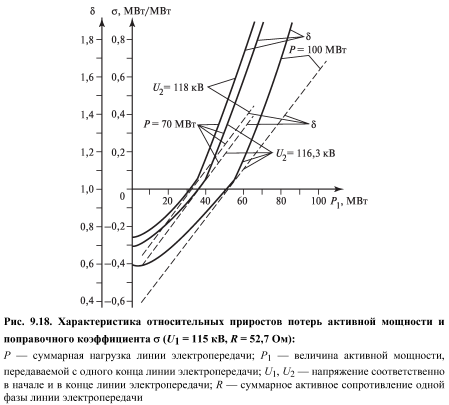
В процессе оптимизации должен решаться ряд взаимосвязанных задач:  • выбор оптимального распределения электрических нагрузок энергообъединения;  • выбор оптимального состава работающего оборудования;  • оптимальное планирование ремонтов энергооборудования;  • выбор оптимального распределения тепловых нагрузок районов теплоснабжения и др.  В настоящее время при наличии больших энергетических систем (например, ЕЭС) в России решение этих задач возможно методом декомпозиции, применяемым при расчетах больших систем. В этом случае расчет проводится поэтапно в соответствии с иерархической структурой диспетчерского управления ЕЭС России.  Существующие методы решения рассматриваемых задач могут быть разделены на две группы:  • методы вариационного исчисления;  • оптимизационные методы математического программирования.   Первая группа методов исследует экстремум функционала. Им могут быть суммарный расход топлива (в тоннах условного топлива) или затраты на производство электроэнергии, зависящие от ряда функций и учитывающие непрерывное изменение показателей во времени. Экстремум функционала определяется системой дифференциальных уравнений Лагранжа. Вторая группа методов основана на сравнении суммарных расходов топлива (в тоннах условного топлива) или денежных затрат при различных вариантах распределения электрических нагрузок или составах работающего оборудования.  При условии наивыгоднейшего распределения электрических нагрузок между электростанциями, входящими в энергообъединение в качестве критерия оптимизации рассмотрим сначала минимум расхода топлива в энергообъединении.  Условия допустимости оптимального режима использования электростанций в энергообъединении следующие.  1. Выполнение в каждый момент времени баланса мощностей энергообъединения, МВт:

Р₁+Р₂+Р₃+...+Р_n+Р_n+1+...+Р_m+Р_г1+...+Р_гn+ +Р_а1+...+Раn=∑Рн+ Р        (9.21)  или W=Р₁+Р₂+Р₃+...+Р_n+Р_n+1+...+Р_m+Р_г1+...+Р_гn+ +Р_а1+...+Р_аn--∑Р_н - Р=0,          (9.22)

где Р₁, Р₂, ..., Р_n - генерируемые активные мощности тепловых электростанций, не имеющих ограничений по расходу топлива в данный момент времени, МВт; Р_n+1, ..., Р_т --- то же для тепловых электростанций, имеющих ограничения по расходу топлива, МВт; Р_г1, ..., Р_{г n} --- то же для гидростанций, МВт; Р_{а 1}, ..., Р_{а n} - то же для атомных станций, МВт; ∑Р_н --- суммарная активная нагрузка потребителей этих электростанций (включая расход на собственные нужды станций и сетей), МВт;  Р --- потери активной мощности в электрической сети, МВт.  2. Обеспечение (п + 1), ..., т-й тепловыми электростанциями заданных ограничений по суточным расходам условного топлива, т у.т/сут:

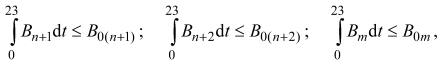
где Вп + 1, Вп + 2, ..., Вт --- часовые расходы условного топлива (п + 1), (п + 2), ..., т-й тепловыми электростанциями, т/ч; B0 (n + 1), B0 (n + 2), ..., B0т --- величины ограничений по суточным расходам топлива этими же станциями.

3. Обеспечение использования гидростанциями заданных суточных расходов воды на энергетические нужды, м³/сут:

где Q_r1, Q_r2, ..., Q_rn --- часовые расходы воды 1, 2, ..., n-й гидростанциями на энергетические нужды, м3/ч; Q_{0г 1}, Q_{0г 2}, ..., Q_{0г n} -  заданные суточные расходы воды этими же станциями, м³/сут. 4. Обеспечение атомными электростанциями суточной экономии органического топлива не меньше заданной, т у.т/сут:

где В_а1, В_а2, ..., В_аn --- суточная экономия органического топлива за счет использования электроэнергии 1, 2, ..., п-й атомной электростанцией, выраженная в т у.т.; B_{0 а1}, B_{0 а2}, ..., B_{0 а n} --- величины ограничений по суточной экономии органического топлива этими же станциями. Минимум расхода условного топлива энергообъединением находится  при выполнении условий допустимости как экстремум функционала

где В₁, В₂, ..., В_n --- часовые расходы условного топлива 1, 2, ..., n-й тепловымиэлектростанциями, т/ч;λ_n+1,λ_n+2, ...,λ_m,λ_г1, ...,λ_{г n}, λ_а1,..., λ_{а n} - некоторые постоянные множители Лагранжа; λ t --- множитель, являющийся функцией времени. Продифференцируем подынтегральное выражения по переменным Р₁,Р₂, ...,Р_n,Р_n+1 ит.д.:

Выразив производные через относительные приросты, перепишем уравнения (9.23) в виде

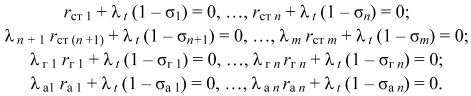
Отсюда

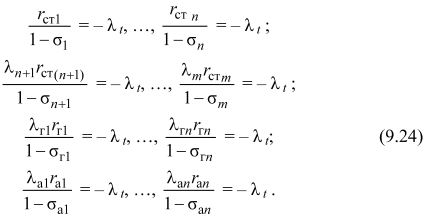
Следовательно, для обеспечения распределения электрической нагрузки между отдельными электростанциями (конденсационными, ТЭЦ, гидроэлектростанциями, атомными электростанциями) на минимум суммарного расхода топлива энергообъединением необходимо, чтобы в каждый момент времени выполнялось следующее условие:

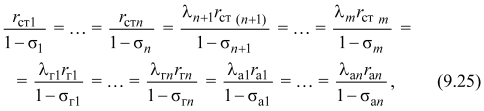
где rст1, rст2, ..., rст п --- относительные приросты расхода условного топлива на 1, 2, ..., п -й тепловой электростанции (нетто), т у.т/(МВт·ч); rст (п+1), ..., rст т --- относительные приросты расхода условного топлива на п + 1, ..., т-й тепловых электростанциях, которые должны израсходовать определенное количество топлива (нетранспортабельные горючие отходы промышленного предприятия) или теплоты вторичных энергоресурсов, т у.т/(МВт·ч); rг1, ..., rгп --- относительные приросты расхода воды на 1, 2, ..., п-й гидростанции, (м3/с)/МВт; rа 1, ..., rа п --- относительные приросты расхода ядерного топлива на 1, 2, ..., п-й атомной электростанции, выраженные в тоннах условного топлива, т у.т/(МВт·ч); λ п + 1, ..., λ т --- безразмерные коэффициенты, используемые для обеспечения режимов на (п + 1), ..., т-й тепловых электростанциях, при которых ими расходуется заданное количество топлива или теплоты вторичных энергоресурсов; λг1, ..., λгп --- коэффициенты, характеризующие изменение расхода условного топлива в энергосистеме под влиянием изменения расхода воды на 1, 2, ..., п-й ГЭС, (т у.т/ч)/(м3/с); λа1,..., λап --- безразмерные коэффициенты, необходимые для обеспечения определенного (наибольшего) использования 1, 2, ..., п-й атомной электростанции (с учетом ограничения по минимальной мощности реактора, вызываемого эффектом «отравления»);

Изменение режима работы отдельных электростанций сказывается главным образом на топливной составляющей себестоимости электроэнергии в энергосистеме. Поэтому достижение минимума затрат на топливо означает и минимум затрат на производство электроэнергии. При одинаковых удельных затратах на одну тонну условного топлива на всех тепловых электростанциях оптимальный режим работы электростанций энергосистемы соответствует минимальным затратам на это топливо. При различных удельных затратах на топливо, присущих отдельным электростанциям данной энергосистемы, для достижения минимума себестоимости электроэнергии необходимо, чтобы в каждый момент времени существовало равенство:

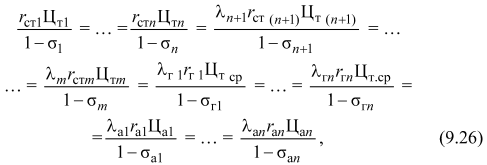
где Цт1, ..., Цтп, Цт(п+1), ..., Цтт --- удельные затраты (цены) на условное топливо на 1, 2, ..., п, (п+1), ..., т-й тепловой электростанции, руб/т у.т.; Цт.ср --- средние удельные затраты на условное топливо на тепловых электростанциях, нагрузка которых меняется с изменением нагрузки гидростанций, руб/т у.т.; Ца1, ..., Цап --- удельные затраты на ядерное горючее, выраженное в тоннах условного топлива, руб/т у.т. Если принять удельные затраты на топливо одной из электростанций за базисные, то, разделив равенство (9.26) на Цт i, получим:

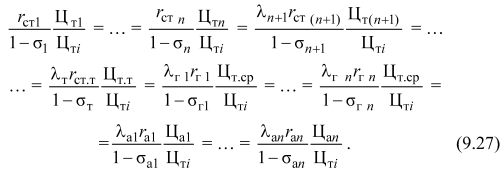
Таким образом, для перехода от критерия минимума расхода топлива к критерию минимума себестоимости электроэнергии в энергосистеме или объединении энергосистем необходимо значения относительных приростов расхода топлива умножить на отношение удельных затрат на топливо на данной станции к аналогичному показателю  на базовой электростанции. Причем если (Цт/Цт i) > 1, то на данной электростанции для обеспечения минимума себестоимости электроэнергии необходимо снизить нагрузку сравнительно с ее режимом на минимум расхода топлива. Если (Цт/Цт i) < 1, то на данной станции необходимо повысить нагрузку по сравнению с режимом, обеспечивающим минимум расхода топлива. Коэффициенты λг, λт, λа устанавливаются итеративным или иным методом исходя из условия полного использования заданного суточного расхода воды на ГЭС, определенного количества топлива на ТЭС, имеющей ограничения по расходу топлива, обеспечения определенного (наибольшего) использования ядерного топлива атомной электростанции.  Перераспределение электрической нагрузки между электростанциями ведет к изменению потерь электроэнергии в электрических сетях, связывающих эти станции между собой, и, следовательно, к изменению расхода топлива (затрат на топливо) в энергосистеме. Учет изменения потерь в электрических сетях приводит к необходимости умножения относительных приростов расхода топлива электростанций на поправочный коэффициент 1/ (1 -- σ). Суммируя нагрузки отдельных станций при одинаковых значениях относительных приростов расхода топлива, найдем электрические нагрузки энергосистемы, соответствующие этим относительным приростам. Так устанавливается связь между нагрузкой энергосистемы и нагрузкой каждой станции. Сложность оптимизации использования производственных мощностей электростанций и потребность в учете меняющихся условий и ограничений приводят к необходимости применения ЭВМ. Определение оптимальных режимов использования производственных мощностей выполняется не только в эксплуатационных условиях, но и при проектировании развития энергетики.