35. Средняя хронологическая величина.

(материал из интернета, в учебнике, практикуме и лекциях информации нет)

Средняя гармоническая представляет собой величину, обратную средней арифметической, и рассчитывается из обратных значений прямых величин (значений признака).

Средняя гармоническая простая. Если объёмы явлений, т.е. произведения Хi ×fi по каждой единице равны, то для расчёта средней применяется формула средней гармонической простой:

Средняя гармоническая взвешенная. Когда статистическая информация не содержит частот (fi ) у отдельных вариантов (X), а представлена как их произведение Mi=(Xi × fi), то для расчёта средней применяется формула средней гармонической взвешенной: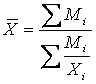

Средняя взвешенная используется, если неравные интервалы времени между уровнями неравны и известно время, в течение которого сохранялось каждое значение х.

36. Понятие и сущность вариации. Значение её изучения.

При изучении социально-экономических явлений и процессов статистика встречается с разнообразной вариацией признаков, характеризующих отдельные единицы совокупности. Величины признаков колеблются под воздействием различных причин и условий, называемых в статистике факторами. Вариация зависимого признака, образовавшиеся под действием всех без исключения влияющих на него факторов, называется общей вариацией. Вариация, порождаемая существенными факторами, носит название, систематической вариацией. Вариация, обусловленная случайными факторами, называется случайной вариацией.

Исследование вариации является составным элементом статистического анализа, позволяющим оценить колебания значений изучаемого признака, взаимосвязь его с другими признаками. Статистические показатели, характеризующие вариацию, служат критерием типичности рассчитанных по совокупности средних величин, используются в определении ошибок выборочных характеристик.

37. Ряды распределения: основные элементы, виды и графическое изображение.

Рядом распределения в статистике называется ряд цифровых показателей, представляющих распределение единиц совокупности по одному существенному признаку, разновидности которого расположены в определённой последовательности.

Состоит из двух элементов: вариантов(групп по выделенному признаку) и частот(численности групп)+ частности(частоты, выраженные в долях единицы)

Виды. В зависимости от признака: 1. атрибутивный ряд(построенный по качественным признакам) 2. вариационный ряд(построенный по количественному признаку). В зависимости от характера: 1. дискретный(распределение единицы совокупности по дискретному признаку) 2. интервальный(целесообразно при непрерывной вариации признака, а так же если дискретная вариация проявляется в широких пределах).

Анализ рядов распределения наглядно можно проводить на основе графического изображения:

• Полигон используется при изображении дискретных вариационных рядов. для его построения в прямоугольной системе координат по оси абсцисс откладываются ранжированные значения варьирующего признака, а по оси ординат наносится шкала для выражения величины частот. Полученные на пересечении точки соединяются и получают ломанную линию, называемую полигоном частот.

• Гистограмма применяется для изображения интервального вариационного ряда. При построении гистограммы на оси абсцисс откладываются величины интервалов, а частоты изображаются прямоугольниками, построенными на соответствующих интервалах.

• Кумулятивная кривая для графического изображения вариационных рядов. На оси абсцисс откладываются варианты ряда, а на оси ординат - накопленные частоты, затем эти перпендикуляры соединяют и получают ломанную линию. Можно построить кумулятивное распределение "не меньше чем" - кумулята, а можно "больше чем" - огива.