32. Понятие, сущность и значение средних величин.

Понятие: это обобщающие показатели, в которых проявляются общие, закономерные черты, свойственные для всей совокупности изучаемого явления.

Сущность: они показывают типичное распространение признаков группы, взаимопоглощая отклонения, обусловленные действием случайных факторов, и учитывают изменения, вызванные действием основных факторов.

Значение: погашаются индивидуальные различия в величине признака, которые возникают по тем или иным причинам у отдельных единиц изучаемой совокупности, и, наоборот, определяется уровень варьирующего признака, типичный для большинства единиц данной совокупности.

Виды:

1. Степенные (простая, взвешенная)

2. Структурные

Исходное соотношение средней = Суммарное значение/Объем совокупности

33. Средняя арифметическая величина: сущность, значение, формы и методы расчета. Условия применения. Другие виды средних.

Средней арифметической величиной называется такое среднее значение признака, привычислении которого общий объем признака в совокупности сохраняется неизменным.

Иначе можно сказать, что средняя арифметическая величина -среднее слагаемое. При еевычислении общий объем признака мысленно распределяется поровну между всеми единицами совокупности. Например, средняя заработная плата или средний доход работников предприятия - это такая сумма денег, которая приходилась бы на каждого работника, если бывесь фонд оплаты труда (или все доходы, направленные на личное потребление) был распределен между работниками поровну.

Исходя из определения, формула средней арифметической величины имеет вид:

По  этой формуле вычисляются средние величины первичных (объемных) признаков, если известны индивидуальные значения признака. Если изучаемая совокупность велика, исходная информация чаще представляет собой ряд распределения или группировку. Тогда используется формула средней взвешанной, где х - отдельные варианты значения признака, f - веса или частота появления признака.

                ,

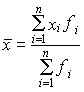В качестве весов выступают здесь числа единиц совокупности в разных группах. Название «вес» выражает тот факт, что разные значения признака имеют неодинаковую «важность» при расчете средней величины.

Как видим, средняя арифметическая величина может быть дробным числом, если даже индивидуальные значения признака могут принимать только целые значения (дискретный признак). Ничего «предосудительного» для метода средних в этом не заключено; из сущности средней не вытекает, что она обязана быть реальным значением признака, которое могло бывстретиться у какой-либо единицы совокупности.

Также выделим такие виды средних, как гармоническая, геометрическая, квадратическая, кубическая.

34. Средняя гармоническая величина: сущность, значение, формы и методы расчета. Условия применения. Другие виды средних.

Средняя гармоническая является преобразованной формой средней арифметической. Средняя гармоническая используется, когда статистическая информация не содержит данных о частотах по отдельным вариантам совокупности, но известны произведения частот на их веса. Общая формула средней гармонической взвешенной имеет следующий вид: х - величина варьирующего признака, w - произведение варьирующего значения признака на его веса (xf) Очевидно, что вместо средней гармонической всегда можно рассчитать среднюю арифметическую, но для этого сначала нужно определить веса отдельных значений варьирующего признака. В том случае, если общие объемы явлений, т.е. произведения признаков на их веса равны, применяется средняя гармоническая простая: х - отдельные значения признака (варианты), п - общее число вариант. Средняя гармоническая взвешанная:

Также выделим такие виды средних, как арифметическая, геометрическая, квадратическая, кубическая.