1 Деление отрезка в данном отношении
Дано: точка
лежит на прямой, проходящей через две
данные точки
и
и дано отношение
. (1)
Найти координаты точки
(рисунок 16).
|
Рисунок 16 |
Решение. Введем векторы
и
,
то есть
и
.
Из равенства (1) следует, что
, (2)
тогда равенство (2) примет вид
.
Но равные векторы имеют равные координаты, тогда
.
Окончательно:
,
. (3)
Эти формулы называются формулами деления отрезка в данном отношении. Если точка середина отрезка , то
,
тогда координаты середины отрезка равны полусумме координат концов отрезка, то есть
,
.
2 Прямая на плоскости
Утверждение. Любое уравнение первой степени на плоскости – есть прямая.
Уравнение
(4)
есть общее уравнение прямой.
При
уравнение
.
Переобозначив
получим
– это прямая, параллельная оси
,
если
,
то
.
Переобозначим
,
тогда
– это прямая, параллельная оси .
– уравнение оси
(оси абсцисс).
– уравнение оси
(оси ординат).
эЧтобы убедиться лежит ли точка
на прямой, необходимо подставить
координаты точки
в уравнение этой прямой.
Пример 1. Принадлежат ли точки
и
прямой
.
Решение. Точка принадлежит прямой, так как
,
а точка
не принадлежит прямой, так как
.
Чтобы узнать координаты точки пересечения двух прямых, нужно совместно прорешать систему уравнений, определяющих эти прямые
.
Если
,
то есть коэффициенты в уравнениях прямых не пропорциональны, то прямые пресекаются в одной точке.
Если коэффициенты при неизвестных в уравнениях прямых и свободные члены пропорциональны, то прямые сливаются (система имеет бесчисленное множество решений).
Если коэффициенты пропорциональны, а свободные члены нет, то прямые параллельны (система решений не имеет).
Из уравнения (4) выразим « »
. (5)
Переобозначим через
,
,
тогда уравнение (5) примет вид:
(8)
– уравнение прямой с угловым
коэффициентом
,
где
– угол между прямой и положительным
направлением оси
,
и «
»
– отрезок
,
где точка
,
точка
(рисунок 17).
|
Рисунок 17 |
Пусть прямая
проходит через точку
,
тогда координаты этой точки удовлетворяют
уравнению прямой (7) тождественно, то
есть
. (8)
Вычтем из равенства (7) равенство (8), получим
. (9)
Это уравнение прямой, проходящей
через точку
с угловым коэффициентом
.
Пусть прямая проходит через две точки
и
.
Возьмем текущую точку , лежащую на этой же прямой (рисунок 18).
|
Рисунок 18 |
Векторы
и
лежат на одной прямой. Координаты их
пропорциональны, то есть
. (10)
Это уравнение прямой, проходящей через две точки.
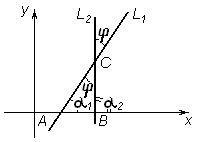
Угол между двумя прямыми и условия параллельности и перпендикулярности двух прямых
Пусть прямые
и
имеют угловые коэффициенты
и
(рисунок 19).
|
Рисунок 19 |
В
как внешний угол, угол
,
тогда
,
если только
.
Тогда
,
но
;
,
поэтому
(11)
Если
,
то
и
,
а это когда числитель дроби (11) равен
нулю, то есть, если прямые параллельны,
то
.
не существует при
.
А это возможно, когда знаменатель дроби
(11) равен нулю, то есть
(13)
– это условие перпендикулярности двух прямых.
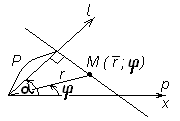
Полярное уравнение прямой
Полярное уравнение прямой можно
определить, указав расстояние
от полюса
до данной прямой и угол
между полярной осью
и осью
,
проходящей через полюс
перпендикулярно данной прямой (рисунок
20).
|
Рисунок 20 |
Для любой точки
на данной прямой имеем:
,
но
.
Значит
(14)
есть уравнение прямой в полярных координатах.
Нормальное уравнение прямой
Перепишем уравнение (14) в виде:
.
Учитывая, что в полярной системе координат
,
получим уравнение
, (16)
которое называется нормальным уравнением прямой.
(рисунок 21).
|
Рисунок 21 |
Тогда уравнение (16) можно переписать в виде
. (17)
Чтобы уравнение (4) привести к виду (17)
надо обе части его умножить на нормирующий
множитель
,
знак которого выбирают противоположным
знаку свободного члена в уравнении (4).
Чтобы найти расстояние от любой точки до прямой надо в нормальное уравнение прямой подставить координаты этой точки, то есть
или
.