6.4.3 Приведение к простейшему виду уравнений центральных линий второго порядка
Пусть дано уравнение (16), определяющее центральную линию второго порядка. И пусть
.
Перенесем начало координат в центр , преобразуя уравнение (16) по формулам:
,
.
Получим:
, (17)
где
.
Далее упрощение уравнения (17) достигается при помощи преобразования координат:
, (18)
соответствующего повороту осей на угол . Где выбирается так, что
. (19)
Отсюда находим .
Тогда в новых координатах уравнение линии примет вид:
, (20)
где
;
.
Из равенства (19) можно определить только
,
а в формуле (18) участвуют
и
,
поэтому:
;
.
Причем между коэффициентами (16) и (20) интересные соотношения:
,
.
Замечание. При этом, если
,
то кривая эллиптического типа.
Если
– гиперболического, а если
,
то параболического.
Пример 3 (Клетеник №676). Привести к каноническому виду
.
Решение.
1)
;
;
;
;
;
.
Находим
.
Следовательно, кривая гиперболического типа.
2) Решаем систему
,
то есть
,
,
,
;
,
.
Произведем параллельный перенос осей с помощью преобразования
,
.
Тогда уравнение примет вид:
. (21)
Найдем угол поворота осей координат, воспользовавшись уравнением (19):
.
и
.
.
По формулам (18) находим
и
,
.
Подставив эти новые координаты в уравнение (21) и выполнив тождественные преобразования, получим
,
,
.
6.4.4 Приведение к простейшему виду параболического уравнения
Пусть уравнение (16)
параболического типа, то есть
,
то есть линия (16) либо не имеет центра, либо имеет бесконечное множество центров.
Поэтому упрощение параболического уравнения лучше начать с поворота координатных осей, то есть сначала преобразовать уравнение при помощи формул (18). Угол так же ищем из (19). Тогда в новых координатах уравнение будет:
или
.
Далее параллельный перенос.
Пример 4 (№689).
.
Решение.
;
;
;
;
;
.
– кривая параболического типа.
;
;
.
Из уравнения (19):
находим
,
.
Тогда
,
,
.
Тогда по формуле (18)
,
.
Подставим эти координаты в данное уравнение:
преобразуем:
выделим слева полный квадрат:
.
Сделаем замену:
,
тогда
– каноническое уравнение параболы, которое получено путем двух последовательных преобразований:
1. Поворота осей координат на угол
:
; .
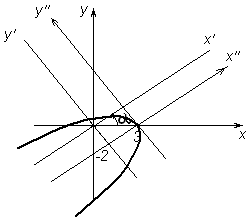
2. Путем параллельного переноса осей координат (рисунок 41):
.
|
Рисунок 41 |
6.4.5 Второй способ приведения уравнений эллипса и гиперболы к каноническому виду через собственные числа и собственные векторы квадратичной формы
Рассмотрим на примере.
Пример 5 (676).
.
.
Решение.
1. Выделим квадратичную форму в уравнении:
,
.
2. Составляем матрицу этой квадратичной формы:
,
– кривая гиперболического типа.
3. Находим собственные числа и собственные векторы этой матрицы. Для этого составляем характеристичекое уравнение:
,
.
4. Находим координаты собственных векторов.
При
.
При
.
5. Нормируем векторы
и
.
Для этого находим их длину:
.
6. Находим координаты единичных векторов:
и
.
7. Составляем ортонормированную матрицу (координаты единичных векторов записаны в столбец):
.
8. Переходим к новым координатам.
Из первой строки матрицы
имеем:
.
Из второй строки матрицы :
.
9. Новые координаты подставим в исходное
уравнение. После тождественных
преобразований получаем в квадратичной
форме коэффициент при «
»
равен меньшему собственному числу (
),
а коэффициент при «
»
равен большему собственному числу (
).
Слагаемое с «
»
исчезает. Об этом надо помнить и
пользоваться, так что новые координаты
в исходное уравнение подставлять только
в оставшуюся от квадратичной формы
часть, то есть:
.
После приведения подобных, имеем:
,
,
,
.
Данная линия представляет собой гиперболу
с центром в точке
и действительной осью
.