Векторная алгебра
1 Основные понятия
Величины, встречающиеся в механике, физике и других прикладных науках, могут быть разделены на два типа: скалярные и векторные. Величины, которые определяются только одним числовым значением, называются скалярными или скалярами (например, масса, время, температура, цена и т. д.). Величины, для определения которых требуется задать кроме числа еще и направление, называются векторными (например, скорость, ускорение, сила и т. д.). Геометрически их изображают вектором.
Определение 1. Вектором называется
направленный отрезок, то есть отрезок
прямой с указанием точек начала
и конца
.
Обозначать вектор в этом случае будем
так:
(первая буква
– начало, вторая –
– конец вектора) или одной буквой
,
которую пишут в конце вектора (рисунок
1).
|
Рисунок 1 |
Длину вектора (или модуль вектора)
обозначают так:
,
.
Определение 2. Если длина вектора
равна единице, то он называется единичным
или ортом. Обозначается –
.
Определение 3. Если у вектора начало
и конец совпадают, то его длина равна
нулю и его называют нулевым, например,
.
Направление нулевого вектора не
определено.
Определение 4. Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными (параллельными) – рисунок 2.
|
Рисунок 2 |
На рисунке 2 векторы
,
и
коллинеарны, при этом векторы
и
одинаково направлены (
),
а векторы
и
,
и
противоположно (
,
).
В математике обычно рассматривают свободные векторы, то есть когда положение их начала не играет никакой роли.
Определение 5. Векторы и называются равными, если они имеют одинаковую длину, параллельны и одинаково направлены. Кратко
,
.
То есть вектор равен , если он может быть получен при помощи параллельного переноса.
Определение 6. Векторы, лежащие в одной плоскости (или в параллельных плоскостях), называются компланарными.
Очевидно, что любые два вектора компланарны, а три вектора не всегда можно «уложить» в одну плоскость.
2 Линейные операции над векторами
К линейным операциям над векторами относятся: сложение векторов и умножение вектора на число.
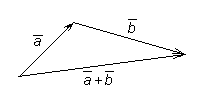
Определение 1. Сумой
двух векторов
и
называется новый вектор, который идет
из начала вектора
в конец вектора
,
при условии, что вектор
приложен к концу вектора
(правило треугольника) – рисунок 3.
|
Рисунок 3 |
Иногда два вектора удобнее складывать
по правилу параллелограмма. Для
этого векторы переносят так, чтобы
начала их были в одной точке
.
Затем строят параллелограмм со сторонами,
равными
и
.
Вектор
будет вектор, совпадающий с диагональю
этого параллелограмма, идущий из общего
начала
и
(точки
).
Это
(рисунок 4).
|
Рисунок 4 |
Пусть требуется сложить
векторов
,
,
.
Суммой этих векторов будет вектор
,
соединяющий начало
,
первого вектора, с концом последнего
вектора
при условии, что начало каждого совмещено
с концом предыдущего (рисунок 5).
|
Рисунок 5 |
Определение 2. Разностью
двух векторов
и
называется вектор, который в сумме с
вектором
составляет вектор
.
Если два вектора
и
приведены к общему началу, то разность
их
есть вектор, идущий из конца
(«вычитаемого») к концу
(«уменьшаемого»). Это на рисунке 4
диагональ
.
Два вектора равной длины, лежащие на
одной прямой и направленные в
противоположные стороны, называются
взаимнообратными: если один из них
обозначается символом
,
то другой обозначается символом
.
Тогда
.
Таким образом, построение разности
равносильно прибавлению к «уменьшаемому»
вектору, обратного «вычитаемому».
Определение 3. Произведением
вектора
на число
(или также
)
называется вектор, модуль которого
равен произведению модуля вектора
на модуль числа
;
он параллелен вектору
или лежит с ним на одной прямой и направлен
так же, как вектор
,
если
– число положительное, и противоположно
вектору
,
если
– число отрицательное (рисунок 6).
|
Рисунок 6 |
Любой вектор может быть представлен в виде произведения двух сомножителей – его длины и единичного вектора того же направления, что и вектор , то есть
или
.
Теорема 1. Два ненулевых вектора
и
параллельны тогда и только тогда, когда
существует такое единственное число
,
что
.
Это необходимое и достаточное условие
коллинеарности двух векторов.
Справедливы легко проверяемые свойства:
1)
,
2)
,
3)
,
4)
,
5)
.
Эти свойства позволяют выполнять действия с векторными выражениями так же, как и с алгебраическими. Например,
.