5 Расчет параметров катушек индуктивности без сердечника

Индуктивность однослойной катушка индуктивности без сердечника (соленоид), чертеж которой приведен на рис. 3,а, рассчитывается по формуле:

. (1)

Если размеры катушки выражены в санти­метрах, то индуктивность, рассчитанная по формуле, имеет размерность микроген­ри.

Точность полученного значения находится в пределах 1% для катушек, длина которых l >2/Зr.

Задание 2. Определите индуктивность катушки диаметром 1,27 и длиной 5,08 см, состоящей из 20 витков.

Задание 3. Вычислите количество витков у катушки, индуктивность которой составляет 20 мкГн, диаметр 5, а длина 3,8 см.

Часто однослойные катушки наматывают очень плотно, и в этом случае количество витков на единицу длины (р) определяется размером провода и толщиной изоляции. Длина катушки . Подставляя это выражение в формулу (1), получим:

(2)

Задание 4. Определите количество витков, требуемое для обмотки однослойной катушки, индуктивность которой равна 120 мкГн, диаметр 2,5 см, при условии, что катушка выполнена из плотно намотанного эмалированного провода (число витков на единицу длины составляет 14,6 витков/см). Определите длину катушки.

Для катушек, длина которых находится в интервале 2/Зr < l < r/10, уравнение (1) принимает вид:

(3)

При этом точность решения находится в пределах 2%.

Задание 5. Определите индуктивность соленоида без сердечника диаметром 10 и длиной 2,5 см, состоящего из 5 витков.

Индуктивность катушки с многослойной плотной обмоткой (каждый слой намотан плотно и рас­полагается непосредственно над предыдущим слоем – рис.3, в) рассчитывается по формуле:

(4)

где r – средний радиус, см; l – длина, см; d – радиальная толщина обмотки, см; N – количество витков.

Задание 6. Вычислите индуктивность катушки с многослойной обмоткой, состоящей из 400 витков, если средний радиус r = 2,5 см, длина обмотки l = 2 см, радиальная толщина d = 1,2 см.

Большинство прямоугольных много­слойных катушек индуктивности имеют об­мотку универсального или галетного типа (рис. 4, б) – про­вод наматывается не перпендикулярно обра­зующей каркаса, а под некоторым углом к ней. Как только провод доходит до края ка­тушки, направление его укладки меняется.

Такая конструкция обусловлена соображе­ниями механической прочности, уменьшения распределенной емкости и увеличения доб­ротности. Катуш­ка, имеющая форму, показанную на рис. 3, в, но с универсальной обмоткой, обладает приблизительно на 10% большей индуктивностью, чем получается из расчета по формуле (4) при одном и том же количе­стве витков.

П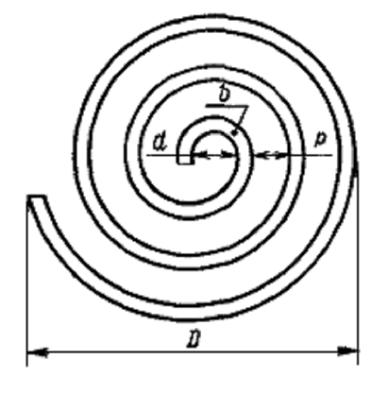 лоская круговая спираль рассчитывается по формуле:

(5)

где l — число витков спирали;

(6)

(7)

есть средний радиус спирали. В формуле (5) все размеры даны в санти­метрах, индуктивность — в микрогенри, логарифмы нату­ральные.

Для случая, когда d = 0, т.е. когда спираль начинает­ся от центра, формула (5) упрощается: L = 0,00345·D·N². (8)

Задание 7. Рассчитайте индуктивность представленных образцов плоских катушек индуктивности.