МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

КАЛУЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИМ. К.Э. ЦИОЛКОВСКОГО

___________________________________________________________

М.Ю. Виноградская,

В.Г. Виноградский,

Н.В. Кравцова

Компьютерное и математическое

моделирование

Учебно - методическое пособие

Калуга, 2011

УДК 519.711.3

ББК 32.973.26-018.2

В-49

Печатается по решению

кафедры информационных технологий

(протокол №3 от 9.11.2011 года)

Печатается за счет средств автора

Рецензент: Комарцова Л.Г. - докт.тех.наук, проф. МГТУ им. Н.Э. Баумана

Виноградская М.Ю., Виноградский В.Г., Кравцова Н.В. Компьютерное и математическое моделирование. Учебно - методическое пособие / Виноградская М.Ю., Виноградский В.Г., Кравцова Н.В. – Калуга: Издательство «Эйдос» (ИП Кошелев А.Б.), 2011. – 71 с.

Учебно - методическое пособие подготовлено в соответствии со стандартом ВПО. В пособии представлен теоретический и практический материал для изучения курса "Компьютерное и математическое моделирование".

Пособие предназначено для студентов заочной формы обучения вузов по специальности «технология и предпринимательство».

© Виноградская М.Ю., Виноградский В.Г., Кравцова Н.В.

Основные теоретические вопросы дисциплины

Слово "Модель" происходит от латинского modus (копия, образ, очертание).

Модель — это материальный или мысленно представляемый объект, который в процессе исследования замещает объект-оригинал так, что его непосредственное изучение дает новые знания об объекте-оригинале.

Моделирование - замещение одного объекта другим с целью получения информации о важнейших свойствах объекта - оригинала с помощью объекта-модели. Другими словами, модель - это объект-заменитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала.

Целью моделирования являются получение, обработка, представление и использование информации об объектах, которые взаимодействуют между собой и внешней средой; а модель здесь выступает как средство познания свойств и закономерности поведения объекта.

Классификация моделей

Модели могут быть относительно полными и неполными.

Все модели можно разделить на два класса: вещественные и идеальные. В свою очередь вещественные модели можно разделить на: натурные, физические, математические. Идеальные модели можно разделить на: наглядные, знаковые, математические.

По форме представления информации - физические, математические, логические, иконографические и др. модели систем.

Применительно к естественным и техническим наукам принято различать следующие виды моделирования: Концептуальное моделирование, Физическое моделирование, Структурно-функциональное моделирование, Математическое (логико-математическое) моделирование, Имитационное (программное) моделирование.

По уровню, "глубине" моделирования модели бывают эмпирические - на основе эмпирических фактов, зависимостей, теоретические - на основе математических описаний и смешанные (полуэмпирические) - использующие эмпирические зависимости и математические описания.

Классификация моделей по признакам: Дискретность и непрерывность. Случайность и детерминированность. Матричность и скалярность. Статичность и динамичность.

Моделирование, если отвлечься от областей и сфер применения моделей, может быть трех типов: познавательное, прагматическое и инструментальное.

Свойства модели: конечность; упрощенность; приблизительность; адекватность; информативность.

Жизненный цикл моделируемой системы - Сбор информации об объекте, выдвижение гипотез, предмодельный анализ; Проектирование структуры и состава моделей (подмоделей); Построение спецификаций модели, разработка и отладка отдельных подмоделей, сборка модели в целом, идентификация (если это нужно) параметров моделей; Исследование модели - выбор метода исследования и разработка алгоритма (программы) моделирования; Исследование адекватности, устойчивости, чувствительности модели; Оценка средств моделирования (затраченных ресурсов); Интерпретация, анализ результатов моделирования и установление некоторых причинно - следственных связей в исследуемой системе; Генерация отчетов и проектных (народно - хозяйственных) решений; Уточнение, модификация модели, если это необходимо, и возврат к исследуемой системе с новыми знаниями, полученными с помощью моделирования.

Этапы построения модели

Построение модели может осуществляться двумя способами:

Схема процесса моделирования

Объект -> Модель -> Изучение модели -> Знания об объекте

Для построения моделей используют два принципа: дедуктивный (от общего к частному) и индуктивный (от частного к общему).

В целом, моделирование включает в себя три необходимых этана: анализ объекта исследования, построение (синтез) модели, получение результата и его оценка путем сравнения с объектом. Это этапы - 1. Анализ объекта моделирования, 2. Формирование (синтез) модели, 3. Оценка результатов, Погрешности модели и их оценка - Погрешность постановки задачи. Начальная погрешность. Погрешность метода. Погрешность инструмента. Выводы из численного эксперимента.

Математическое моделирование. Этапы математического моделирования

Сущность этой методологии состоит в замене исходного объекта его "образом" — математической моделью — и дальнейшем изучении модели с помощью реализуемых на компьютерах вычислительно-логических алгоритмов. Этот "третий метод" познания, конструирования, проектирования сочетает в себе многие достоинства как теории, так и эксперимента.

Этапы математического моделирования. На первом этапе выбирается (или строится) "эквивалент" объекта, отражающий в математической форме важнейшие его свойства - законы, которым он подчиняется, связи, присущие составляющим его частям, и т.д. Математическая модель (или ее фрагменты) исследуется теоретическими методами, что позволяет получить важные предварительные знания об объекте. Второй этап — выбор (или разработка) алгоритма для реализации модели на компьютере. Модель представляется в форме, удобной для применения численных методов, определяется последовательность вычислительных и логических операций, которые нужно произвести, чтобы найти искомые величины с заданной точностью. Вычислительные алгоритмы должны не искажать основные свойства модели и, следовательно, исходного объекта, быть экономичными и адаптирующимися к особенностям решаемых задач и используемых компьютеров. На третьем этапе создаются программы, "переводящие" модель и алгоритм на доступный компьютеру язык. К ним также предъявляются требования экономичности и адаптивности.

Процесс построения математических моделей может быть условно разбит на следующие этапы. Конструирование модели начинается со словесно-смыслового описания объекта или явления. Помимо сведений общего характера о природе объекта и целях его исследования эта стадия может содержать также некоторые предположения (невесомый стержень, толстый слой вещества, прямолинейное распространение световых лучей и т.д.). Данный этап можно назвать формулировкой предмодели. Следующий этап - завершение идеализации объекта. Отбрасываются все факторы и эффекты, которые представляются не самыми существенными для его поведения.

После выполнения первых двух этапов можно переходить к выбору или формулировке закона (вариационного принципа, аналогии и т.п.), которому подчиняется объект, и его записи в математической форме. При необходимости используются дополнительные сведения об объекте, также записываемые математически.

Завершает формулировку модели ее "оснащение", формулируется цель исследования модели (найти закон преломления света, достичь понимания закономерностей изменения популяции, определить требования к конструкции ракеты, запускающей спутник, и т. д.).

Построенная модель изучается всеми доступными исследователю методами, в том числе со взаимной проверкой различных подходов. В отличие от рассматриваемых простейших случаев, большинство моделей не поддаются чисто теоретическому анализу, и поэтому необходимо широко использовать вычислительные методы. Это обстоятельство особенно важно при изучении нелинейных объектов, так как их качественное поведение заранее, как правило, неизвестно.

В результате исследования модели не только достигается поставленная цель, но и должна быть установлена всеми возможными способами (сравнением с практикой, сопоставлением с другими подходами) ее адекватность - соответствие объекту и сформулированным предположениям. Неадекватная модель может дать результат, сколь угодно отличающийся от истинного, и должна быть либо отброшена, либо соответствующим образом модифицирована.

Классификация математических моделей. Форма и принципы представления математической модели зависит от многих факторов. По принципам построения математические модели разделяют на: аналитические; имитационные.

В аналитических моделях процессы функционирования реальных объектов, процессов или систем записываются в виде явных функциональных зависимостей. Аналитическая модель разделяется на типы в зависимости от математической проблемы: уравнения (алгебраические, трансцендентные, дифференциальные, интегральные), аппроксимационные задачи (интерполяция, экстраполяция, численное интегрирование и дифференцирование), задачи оптимизации, стохастические проблемы.

Однако по мере усложнения объекта моделирования построение аналитической модели превращается в трудноразрешимую проблему. Тогда исследователь вынужден использовать имитационное моделирование - функционирование объектов, процессов или систем описывается набором алгоритмов. Алгоритмы имитируют реальные элементарные явления, составляющие процесс или систему с сохранением их логической структуры и последовательности протекания во времени.

В зависимости от характера исследуемых реальных процессов и систем математические модели могут быть: детерминированные, стохастические. По виду входной информации модели разделяются на: непрерывные, дискретные. По поведению моделей во времени они разделяются на: статические, динамические. По степени соответствия между математической моделью и реальным объектом, процессом или системой математические модели разделяют на: изоморфные (одинаковые по форме), гомоморфные (разные по форме).

Компьютерное моделирование. Традиционно под моделированием на ЭВМ понималось лишь имитационное моделирование. В настоящее время под компьютерной моделью чаще всего понимают: условный образ объекта или некоторой системы объектов (или процессов), описанный с помощью взаимосвязанных компьютерных таблиц, блок-схем, диаграмм, графиков, рисунков, анимационных фрагментов, гипертекстов и т. д. и отображающий структуру и взаимосвязи между элементами объекта; отдельную программу, совокупность программ, программный комплекс, позволяющий с помощью последовательности вычислений и графического отображения их результатов, воспроизводить (имитировать) процессы функционирования объекта, системы объектов при условии воздействия на объект различных, как правило, случайных, факторов. Такое моделирование - называют имитационным моделированием.

Компьютерное моделирование - метод решения задачи анализа или синтеза сложной системы (объекта, процесса, явления) на основе использования ее компьютерной модели, т.е. модели созданной на ЭВМ. Суть компьютерного моделирования заключена в получении количественных и качественных результатов по имеющейся модели.

Разновидности компьютерного моделирования.

В принципе, все виды моделирования могут быть переведены на компьютерную основу. Виды компьютерных моделей: математическое моделирование и вычислительный эксперимент; экономическое моделирование; графическое (3-хмерное моделирование); информационное моделирование (базы данных и базы знаний) и т.д.

Компьютерное моделирование, вычислительный эксперимент становится новым инструментом, методом научного познания, новой технологией также из-за возрастающей необходимости перехода от исследования линейных математических моделей систем.

Основные функции компьютера при моделировании: роль вспомогательного средства для решения задач, решаемых обычными вычислительными средствами, алгоритмами, технологиями; роль средства постановки и решения новых задач, не решаемых традиционными средствами, алгоритмами, технологиями; роль средства конструирования компьютерных обучающе-моделирующих сред; роль средства моделирования для получения новых знаний; роль "обучения" новых моделей (самообучающиеся модели).

Объекты компьютерного моделирования: экономическая деятельность фирмы или банка, промышленное предприятие, информационно-вычислительная сеть, технологический процесс, любой реальный объект или процесс, например процесс инфляции, или нагрев тела и… любая сложная система или объект.

Модели и моделирование применяются по следующим основным и важным направлениям.

Обучение (как моделям, моделированию, так и самих моделей).

Познание и разработка теории исследуемых систем - с помощью, каких-то моделей, моделирования, результатов моделирования.

Прогнозирование (выходных данных, ситуаций, состояний системы).

Управление (системой в целом, отдельными подсистемами системы, выработка управленческих решений и стратегий).

Автоматизация (системы или отдельных подсистем системы).

В базовой четверке информатики: "модель - алгоритм - компьютер - технология" при компьютерном моделировании главную роль играют уже алгоритм (программа), компьютер и технология (точнее, инструментальные системы для компьютера, компьютерные технологии).

Обзор программных средств моделирования

В настоящее время существует немалое количество математических пакетов. Наиболее распространенные из них – это Mathcad, Matlab, Derive, Eureka, Mathematika, Maple. Данные пакеты многофункциональны. Например, интегрированная система автоматизации математических, физических, химических, электро-радиохимических и прочих научно-технических расчетов «Eureka» позволяет: выполнить типовые математические и экономические расчеты; вычислять производные и интегралы; решать системы уравнений; искать экстремумы; выводить данные в табличной форме; строить по выбору график одной из функций; работать с комплексными числами.

Математический пакет «Derive» является системой символьной математики, т.е. позволяет производить символьные вычисления. Пакет обладает богатыми графическими возможностями. Задания и результаты вычислений представлены на экране в привычной математической записи. Имеет несколько десятков встроенных функций; действия с комплексными числами; решение задач математического анализа: отыскание пределов функций, производных, определенных и неопределенных интегралов, конечных сумм и сумм числовых рядов, бесконечных произведений; операции векторной алгебры; действия с матрицами, вычисление обратной матрицы, собственных значений матрицы. «Derive» имеет библиотеку функций-утилит, предназначенных для решения специальных задач, есть возможность пополнения библиотеки функциями пользователя.

«Matlab» является одной из старейших и проработавших систем автоматизации автоматических расчетов. Своим названием (MATrixLABoratory – «матричная лаборатория») система «Matlab» обязана ориентации на матричные и векторные вычисления. Она выполняет операции над векторами и матрицами даже в режиме простых вычислений без какого-либо программирования. Система содержит средства, особенно удобные для электрорадиотехнических расчетов (операции с комплексными числами, полиномами, обработка данных, анализ сигналов и цифровая фильтрация); содержит также операторы построения графиков в декартовой и полярной системах координат, трехмерных поверхностей. На одном графике данная система может представить множество кривых, различающихся цветом и отличительными символами. Графики «Matlab» выводит в одном или несколько окон. Эта система выполняет все вычисления в арифметике с плавающей точкой, также поддерживает выполнение операций с массивами данных, регулирует сингулярное и спектральное разложения, вычисление ранга и чисел обусловленности матриц, поддерживает работу с алгебраическими полиномами, решение нелинейных уравнений и задач оптимизации, интегрирование в квадратурах, решение дифференциальных и разностных уравнений. В системе реализована удобная операционная среда, которая позволяет формулировать проблемы и получать решения в привычной математической форме, не прибегая к рутинному программированию.

Разновидности экономико-математических моделей

Математические модели в экономике имеют целевое назначение (например, для исследования структуры, функционирования, расхода). Модели структуры предназначены для изучения взаимоположения и связей элементов системы как внутри нее, так и с внешней средой. Такие модели могут быть представлены в виде сетевых моделей, графиков, матриц и др. Модели функционирования предназначены для изучения системы в динамике. Так, модели жизненного цикла изделий изучаются в маркетинге, модели операций применяются для решения конкретных экономических задач (модели анализа, прогнозирования, управления и др.). Модели расхода или прибыли используются при определении технико-экономических показателей систем, оптимизации по отдельным критериям и в других случаях.

При классификации моделей по исследуемым экономическим процессам и содержательной проблематике можно выделить модели макроэкономические и микроэкономические.

Макроэкономические модели строятся на уровне национального хозяйства, а микроэкономические — на уровнях организаций, их объединений и отдельных регионов.

Различают модели дескриптивные и нормативные.

При изучении экономических процессов математические модели рассматриваются в тесной связи с целевыми системами и представляют собой некоторые целостные структуры (назовем их экономико-математическими моделями). Экономико-математические модели (ЭММ) — смешанные модели (логико-математические, математико-иконографические и др.), включающие в себя совокупность математических зависимостей, логических построений, схем, графиков и т.д., связанных в некоторую единую систему, имеющую экономический смысл.

По функциональному применению ЭММ делятся на теоретико-аналитические (используемые в исследованиях общих свойств и закономерностей экономических объектов) и прикладные (применяемые в решении различных зависимостей в экономике, в частности для установления статистических закономерностей экономического поведения социальных групп, вероятных путей развития ка­ких-либо процессов при определенных условиях). Примерами дескриптивных моделей являются производственные функции и функции покупательского спроса, построенные на основе обработки статистических материалов.

По характеру отражения причинно-следственных связей выделяют модели жестко детерминистские и модели, учитывающие случайность и неопределенность. Различают неопределенности, описываемые вероятностными законами, и неопределенности, для описания которых вероятностные методы неприменимы. Второй тип неопределенности гораздо более сложен для моделирования.

По способам отражения фактора времени ЭММ делятся на статические и динамические. В статических моделях все зависимости относятся к одному моменту или периоду вре­мени. Динамические модели характеризуют изменения экономических процессов во времени.

По соотношению внешних и внутренних переменных, включаемых в модель, они могут разделяться на открытые и закрытые. Хотя полностью закрытых и открытых моделей почти не бывает. Большинство ЭММ занимают промежуточное положение и разли­чаются по степени открытости или закрытости.

При рассмотрении сложного объекта, как правило, прибегают к построению моделей его отдельных частей (так называемые детализированные модели). Из детализированных моделей, в свою очередь, составляется общая модель, называемая агрегированной.

ЭММ можно классифицировать и по другим признакам, например по отраслям, направлениям исследований, сложности, используемому математическому аппарату и т.д.

Системный подход при моделировании экономических объектов. Одним из главных принципов моделирования экономических объектов является принцип системности. В моделировании наибольшее значение имеют следующие основные принципы: интегратизма, неопределенности, инвариантности и принцип главных видов деятельности.

Принцип интегратизма заключается в том, что взаимоотношения части и целого характеризуются совокупностью трех элементов: 1) возникновением взаимодействующих систем — связей между частями целого; 2) утратой некоторых свойств части при вхождении в целое; 3) появлением новых свойств у целого, обусловленных свойствами составных частей.

Принцип неопределенности предполагает, что «по краям» экономические процессы расплывчаты и неопределенны. Протекая во времени, они постоянно изменяются, и если нам даже удастся установить какое-либо свойство или качество процесса, то оно действительно только в рассматриваемый момент времени в данной ситуации. Иначе говоря, на микроуровне экономические процессы необходимо рассматривать с учетом случайного изменения факторов.

Принцип неопределенности позволяет также утверждать, что существует уровень факторов, когда их малые отклонения не влекут изменений в состоянии системы. Однако, чем сложнее модель системы, чем глубже мы пытаемся анализировать ее, тем неопределеннее становится решение задачи, а ее результаты тем дальше от практического смысла.

Принцип инвариантности заключается в том, что модель системы должна быть инвариантна для любых организационных форм производства и изменение каких-либо условий не должно изменять существа модели.

Принцип главных видов деятельности состоит в том, что у разных систем существуют «похожие» виды деятельности (управление, регулирование, распределение и т.п.), которые можно выде­лить как стандартные. Они бывают, неизменны на некотором промежутке времени и могут быть описаны некоторыми похожими моделями.

При построении ЭММ следует учитывать характерные особенности экономических моделей: интеграцию научных знаний в экономике, рост количества междисциплинарных проблем; комплексность проблем и необходимость их изучения в единстве экономических, социальных, психологических, технических и других аспектов; усложнение решаемых проблем, усложнение экономических объектов; рост количества связей между объектами в системах; динамичность изменяющихся ситуаций; дефицитность ресурсов; повышение уровня стандартизации моделирования за счет внедрения программных продуктов для компьютерных технологий, разработки новых принципов моделирования и др.

Эти особенности вызывают неизбежность применения системного подхода, поскольку на его основе можно построить качественную ЭММ.

Системный подход — методология исследования объекта и построения его математической модели, когда объект рассматривается как целостный комплекс взаимосвязанных компонентов, имеющий особое единство с внешней средой и представляющий собой подсистему системы более высокого порядка (глобальной системы). Единство системы с внешней средой определяет ее взаимосвязь с действием объективных экономических законов.

При моделировании объектов и представлении их в виде систем необходимо учитывать общие свойства систем, такие как: целостность; делимость; изолированность; устойчивость; разнообразие; идентифицируемость; стабилизация; наблюдаемость; неопределенност; нетождественность отображения; адаптация.

Любая система в процессе перехода от качественных описаний к количественным в некоторый момент достигает такого уровня, когда для фиксации связей в процессе изучения с помощью теории и эксперимента наиболее действенным и плодотворным оказывается использование математического аппарата.

Процесс решения экономических задач включает следующие этапы: 1. Содержательная постановка задачи. 2. Системный анализ. 3. Системный синтез (математическая постановка задачи) 4. Разработка или выбор программного обеспечения. 5. Решение задачи.

Основные системные понятия кибернетической системы

Кибернетическая система - это множество взаимосвязанных объектов - элементов системы, способных воспринимать, запоминать и перерабатывать информацию, а также обмениваться информацией. Система включает также связи между элементами. Элементы и связи между ними могут обладать свойствами (показателями), каждое из которых может принимать некоторое множество значений.

Каждый элемент системы, в свою очередь, может быть системой, которая по отношению к исходной системе является подсистемой. В свою очередь, любая система может быть подсистемой другой системы, которая по отношению к ней является надсистемой.

Средой данной системы называется система, состоящая из элементов, не принадлежащих этой системе. Объединение двух систем есть система, составленная из элементов объединяемых систем. Пересечение двух систем есть система, состоящая из элементов, принадлежащих одновременно обоим этим системам. Объединение системы и ее среды называется система-универсум. Пересечение системы и ее среды называется пустой системой. Она не содержит ни одного элемента.

Для того, чтобы элементы системы могли воспринимать, запоминать и перерабатывать информацию, они должны обладать изменчивостью, т.е. менять свои свойства. Говорят, что элемент может находиться в разных состояниях. Каждый элемент характеризуется набором показателей. При изменении значения хотя бы одного из показателей элемент переходит в другое состояние, т.е. состояние элемента определяется совокупностью конкретных значений показателей элемента. Система в целом также может рассматриваться как элемент, она характеризуется своими показателями и может переходить из одного состояния в другое.

Сигнал есть сообщение о состоянии элемента. Состояние элемента может меняться самопроизвольно, или в результате сигналов и воздействий, поступающих извне системы. Сообщение - это совокупность сигналов. Сигналы, вырабатываемые элементами системы, могут поступать за пределы системы, в этом случае они называются выходными сигналами системы. В свою очередь, на элементы могут поступать сигналы извне системы, они называются входными. Аналогичным образом определяются входные и выходные воздействия.

Структура системы - это совокупность ее элементов и связей между ними, по которым могут проходить сигналы и воздействия. Входами называются элементы системы, к которым приложены входные воздействия или на которые поступают входные сигналы. Входными показателями называются те показатели системы, которые изменяются в результате входного воздействия или сигнала. Выходами называются элементы системы, которые осуществляют воздействие или передают сигнал в другую систему. Выходными показателями называются те показатели системы, изменения которых вызывают выходное воздействие или выходной сигнал, либо сами являются таким воздействием или сигналом.

Классификация кибернетических систем

Классификацию кибернетических систем по двум критериям: степень сложности системы и ее детерминированность. По степени сложности системы бывают: 1. Простые. 2. Сложные. 3. Сверхсложные.

Границы между указанными классами размыты и могут со временем смещаться, например, совершенствование математического аппарата и вычислительной техники позволяет дать описание систем, для которых это раньше было невозможно, или сложное описание сделать простым.

По второму критерию системы делятся на детерминированные и вероятностные.

Все возможные случаи получаются комбинированием указанных классов:

1. Простые детерминированные системы: холодильник с регулятором; система размещения станков в цехе; система автобусных маршрутов; семейный бюджет; расписание занятий факультета;

2. Сложные детерминированные системы: ЭВМ; цветной телевизор; сборочный автоконвейер;

3. Сверхсложные детерминированные системы: шахматы.

4. Простые вероятностные системы: лотерея; система статистического контроля продукции на предприятии;

5. Сложные вероятностные системы: система материально-технического снабжения на предприятии; система диспетчирования движения самолетов вблизи крупного аэропорта; система диспетчирования энергетической системы России;

6. Сверхсложные вероятностные системы: предприятие в целом, включая все его технические, экономические, административные, социальные характеристики; общество; человеческий мозг.

Динамика системы. Состояние системы - это совокупность значений ее показателей. Все возможные состояния системы образуют ее множество состояний. Если в этом множестве определено понятие близости элементов, то оно называется пространством состояний. Движение (поведение) системы - это процесс перехода системы из одного состояния в другое, из него в третье и т.д. Если переход системы из одного состояния в другое происходит без прохождения каких-либо промежуточных состояний, то система называется дискретной. Если при переходе между любыми двумя состояниями система обязательно проходит через промежуточное состояние, то она называется динамической (непрерывной).

Возможны следующие режимы движения системы: 1) равновесный, когда система находится все время в одном и том же состоянии; 2) периодический, когда система через равные промежутки времени проходит одни и те же состояния; Если система находится в равновесном или периодическом режиме, то говорят, что она находится в установившемся или стационарном режиме. 3) переходный режим - движение системы между двумя периодами времени, в каждом из которых система находилась в стационарном режиме; 4) апериодический режим - система проходит некоторое множество состояний, однако закономерность прохождения этих состояний является более сложной, чем периодические, например, переменный период; 5) эргодический режим - система проходит все пространство состояний таким образом, что с течением времени проходит сколько угодно близко к любому заданному состоянию.

Свойства объекта и его поведение зависят от того, каким образом мы его представляем в виде системы. Например, если воздух, находящийся в этой комнате, представить в виде системы молекул, каждая из которых характеризуется своими координатами и скоростью, то поведение такой системы будет эргодично, если же определить его как систему, состоящую из одного элемента, показателями которого являются давление и температура, то такая система находится в равновесном режиме.

Для всех практических задач второй способ определения системы предпочтительнее. Мы получаем простую детерминированную систему, а в первом случае - сверхсложную вероятностную, которую мы не сможем исследовать, а если бы даже смогли, то нигде бы не использовали полученные результаты. Необходимо правильное определение системы и при исследовании экономических объектов, которыми мы желаем управлять. Инструментом исследования объектов для целей выбора оптимальных способов управления является кибернетическое моделирование.

Имитационное моделирование. Имитационными называются математические модели, воспроизводящие алгоритм функционирования исследуемой системы путем последовательного выполнения большого количества элементарных операций. Имитационное моделирование - это совокупность методов алгоритмизации функционирования объектов исследований, программной реализации алгоритмических описаний, организации, планирования и выполнения на ЭВМ вычислительных экспериментов с математическими моделями, имитирующими функционирование РПС в течении заданного периода.

Основное достоинство ИМ: возможность описания поведения компонент (элементов) процессов или систем на высоком уровне детализации; отсутствие ограничений между параметрами ИМ и состоянием внешней среды РПС; возможность исследования динамики взаимодействия компонент во времени и пространстве параметров системы; Эти достоинства обеспечивают имитационному методу широкое распространение. Рекомендуется использовать имитационное моделирование в следующих случаях: Если не существует законченной постановки задачи исследования и идет процесс познания объекта моделирования. Имитационная модель служит средством изучения явления. Если аналитические методы имеются, но математические процессы сложны и трудоемки, и имитационное моделирование дает более простой способ решения задачи. Когда кроме оценки влияния параметров (переменных) процесса или системы желательно осуществить наблюдение за поведением компонент (элементов) процесса или системы (ПС) в течение определенного периода. Когда имитационное моделирование оказывается единственным способом исследования сложной системы из-за невозможности наблюдения явлений в реальных условиях (реакции термоядерного синтеза, исследования космического пространства). Когда необходимо контролировать протекание процессов или поведение систем путем замедления или ускорения явлений в ходе имитации. При подготовке специалистов новой техники, когда на имитационных моделях обеспечивается возможность приобретения навыков в эксплуатации новой техники. Когда изучаются новые ситуации в РПС. В этом случае имитация служит для проверки новых стратегий и правил проведения натурных экспериментов. Когда особое значение имеет последовательность событий в проектируемых ПС и модель используется для предсказания узких мест в функционировании РПС.

Однако ИМ наряду с достоинствами имеет и недостатки: Разработка хорошей ИМ часто обходится дороже создания аналитической модели и требует больших временных затрат. Может оказаться, что ИМ неточна (что бывает часто), и мы не в состоянии измерить степень этой неточности.

Зачастую исследователи обращаются к ИМ, не представляя тех трудностей , с которыми они встретятся и совершают при этом ряд ошибок методологического характера. И, тем не менее, ИМ является одним из наиболее широко используемых методов при решении задач синтеза и анализа сложных процессов и систем.

Одним из видов имитационного моделирования является статистическое имитационное моделирование, позволяющее воспроизводить на ЭВМ функционирование сложных случайных процессов. Статистическая модель случайного процесса - это алгоритм, с помощью которого имитируют работу сложной системы, подверженной случайным возмущениям; имитируют взаимодействие элементов системы, носящих вероятностный характер. При реализации на ЭВМ статистического имитационного моделирования возникает задача получения на ЭВМ случайных числовых последовательностей с заданными вероятностными характеристиками. Численный метод решающий задачу генерирования последовательности случайных чисел с заданными законами распределения получил название "метод статистических испытаний" или "метод Монте-Карло".

Методика статистического моделирования состоит из следующих этапов: Моделирование на ЭВМ псевдослучайных последовательностей с заданной корреляцией и законом распределения вероятностей (метод Монте-Карло), имитирующих на ЭВМ случайные значения параметров при каждом испытании; Преобразование полученных числовых последовательностей на имитационных математических моделях. Статистическая обработка результатов моделирования.

Обобщенный алгоритм метода статистических испытаний представлен на рис.1.

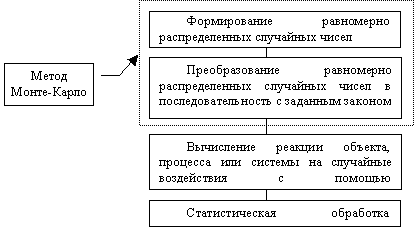
Рис. 1.  Обобщенный алгоритм метода статистических испытаний

Метод Монте-Карло - это численный метод, моделирующий на ЭВМ псевдослучайные числовые последовательности с заданными вероятностными характеристиками.

Операции над моделями. Основными операциями над моделями являются:

Линеаризация. Пусть М=М(X,Y,A), где X - множество входов, Y - выходов, А - состояний системы. Если X, Y, A - линейные пространства (множества), а f, y - линейные операторы, то система (модель) называется линейной. Другие системы (модели) - нелинейные. Нелинейные системы трудно поддаются исследованию, поэтому их часто линеаризуют - сводят к линейным каким-то образом.

Идентификация. Пусть М=М(X,Y,A), A={ai}, ai=(ai1,ai2,...,aik) - вектор состояния объекта (системы). Если вектор ai зависит от некоторых неизвестных параметров, то задача идентификации (модели, параметров модели) состоит в определении по некоторым дополнительным условиям, например, экспериментальным данным, характеризующим состояние системы в некоторых случаях. Идентификация - решение задачи построения по результатам наблюдений математических моделей, описывающих адекватно поведение реальной системы.

Агрегирование. Операция состоит в преобразовании (сведении) модели к модели (моделям) меньшей размерности (X, Y, A).

Декомпозиция. Операция состоит в разделении системы (модели) на подсистемы (подмодели) с сохранением структур и принадлежности одних элементов и подсистем другим.

Сборка. Операция состоит в преобразовании системы, модели, реализующей поставленную цель из заданных или определяемых подмоделей (структурно связанных и устойчивых).

Макетирование. Эта операция состоит в апробации, исследовании структурной связности, сложности, устойчивости с помощью макетов или подмоделей упрощенного вида, у которых функциональная часть упрощена (хотя вход и выход подмоделей сохранены).

Экспертиза, экспертное оценивание. Операция или процедура использования опыта, знаний, интуиции, интеллекта экспертов для исследования или моделирования плохо структурируемых, плохо формализуемых подсистем исследуемой системы.

Вычислительный эксперимент. Это эксперимент, осуществляемый с помощью модели на ЭВМ с целью распределения, прогноза тех или иных состояний системы, реакции на те или иные входные сигналы. Прибором эксперимента здесь является компьютер (и модель!).

В развитии ПО всегда можно выделить два основных направления: - выполнение вычислений; накопление и обработка информации.

Основу информационной системы (ИС) составляет вычислительная система, включающая следующие компоненты: кабельная сеть и активное сетевое оборудование, компьютерное и периферийное оборудование, оборудование хранения данных (библиотеки), системное программное обеспечение (операционные системы, системы управления базами данных), специальное ПО (системы мониторинга и управления сетями) и в некоторых случаях, прикладное ПО. ИС являются обычным продуктом, но имеют ряд существенных отличий от стандартных прикладных программных систем: ИС предназначены для сбора, хранения, обработки информации. Поэтому в основе любой из ИС лежат средства хранения и доступа данных; ИС ориентируются на конечного пользователя, не обладающего высокой квалификацией в области применения ВТ; При разработке ИС приходиться решать следующие задачи: разработка БД, предназначенной для хранения информации; разработка графического интерфейса клиентских приложений; проектирование информационно-вычислительных сетей.

Под ИС понимается прикладная программная подсистема, ориентированная на сбор, хранение, поиск и обработку информации посредством сетевых телекоммуникаций. В общем случае типовые программные компоненты ИС включают в себя: диалог ввода/вывода; логику диалога; прикладную логику обработки данных; логику управления данными; операции манипулирования файлами БД.

В развитии технологии разработки ИС можно выделить 3 существенных изменения: новый подход к программированию – объектно-ориентированное программирование вытеснило модульное; развитие сетевых технологий – локальные ИС вытесняются клиент-серверными и многоуровневыми реализациями ИС; развитие глобальных сетей (Internet) широкое внедрение программирования в экономические системы, активное развитие электронной коммерции.

Классификация ИС. По масштабу: Одиночные; Групповые; Корпоративные. По сфере применения: Системы обработки транзакций - оперативная обработка транзакций, пакетная обработка транзакций; Системы принятия решений - системы поддержания принятия решения, оперативная аналитическая обработка, экспертные системы; Информационно-справочные системы – системы электронной документации, геоинформационные системы, гипертекстовые системы; Офисные ИС - документальные системы, автоматизация делопроизводства, управление документооборотом. По способу организации можно выделить следующие классы: Файл-серверная архитектура; Клиент-серверная архитектура; Многоуровневая архитектура; Интернет-интранет архитектура; Практическая реализация ИС.

Бухгалтерский учет – классическая область применения ИС и наиболее часто реализуемая на сегодняшний день задача. Управление финансовыми потоками – внедрение ИТ в УФП обусловлено критичностью в этой области управления предприятия к ошибкам. Управление складом, ассортиментом, поставками – автоматизированный процесс анализа, отслеживание ассортимента, приносящего наибольшую прибыль. Можно существенно повысить объемы продаж и прибыли предприятия. Управление производственным процессом – представляет собой трудоемкую задачу. Основными механизмами здесь являются планирование и оптимальное управление производственным процессом. Управление маркетингом – осуществление сбора и анализа данных о продукции, фирмах-конкурентах, анализ спроса. Управление документооборотом – является важным процессом деятельности предприятия. Хорошо отлаженная система учета документооборота отражает реально происходящую на предприятии текущую производственную деятельность и дает управляющим возможность оперативного воздействия на нее. Оперативное управление предприятием – ИС строится на основе баз данных, где собирается вся информация о деятельности предприятия: производственная деятельность, маркетинговая деятельность, финансово-экономическая деятельность, менеджмент и т.д. Информационно-рекламная деятельность предприятия – выпуск печатной продукции или управление web-сайтом предприятия.

Управление процессом можно разделить на две области: управление организационно-экономическим процессом и управление технологическим процессом. Соответственно здесь можно выделить два типа ИС: ИС организационно-экономического или административного управления предприятием (ИСП); ИС управления технологическим процессом (ИСТП);. Как правило, в ИСП процессы управления весьма инертны, что позволяет использовать документную форму представления входной информации и дискретный ввод ее в систему. К ИСТП относятся такие системы, которым свойственно управление объектами быстро меняющими свое состояние (управление процессом резанья, плавка метала и т.д.). Для получения необходимых динамических характеристик дискретный ввод и вывод информации в большинстве случаев не применим.

Технологические процессы настолько разнообразны и зависят от такого большого количества факторов, что человек не в состоянии контролировать и воздействовать на все переменные одновременно. Часто на практике приходится иметь дело с системами, в которых комбинируются функции, характерные как для ИСП, так и для ИСТП. В последнее время наметились тенденции к слиянию этих типов ИС в единые интеграционные системы управления, позволяющие обрабатывать всю имеющуюся на предприятии информацию одним информационным комплексом.

ИСП органически включают в себя интегрированные системы обработки данных, главной целью которых является автоматизация информационных процессов на предприятии и усовершенствование форм и организации их выполнения.

Компьютерное моделирование и виртуальная реальность. Компьютерное проектирование позволяет не только создать, но и усовершенствовать сложное изделие, оценить и опробовать его не на реальном предприятии, а в среде виртуальной реальности. Это особенно актуально для дорогостоящих, сложных, уникальных технологических и военно-технических комплексов.

В настоящее время мы наблюдаем все более массированное применение технологий виртуального прототипирования, т.е. процесса создания виртуальной (электронной) модели объекта, предназначенного для последующего производства, ее всесторонней оценки на этапе наличия виртуального прототипа, оптимизации технологических процессов его изготовления. Только после получения удовлетворительных результатов принимается решение об изготовлении физического объекта. Немаловажным также, является и внешний вид изделия, его формы, характеристики - дизайн. Дизайн - это новая область применения компьютерной графики в промышленности. Обычно цель дизайнерской проработки изделия - выбор наиболее удачной концепции внешнего облика изделия из множества вариантов и детальный визуальный анализ выбранной концепции. Если дизайн изделия выполняется с помощью компьютера, это позволяет сократить в несколько раз время, как на дизайнерскую проработку, так и на общий цикл разработки (например, выпуск на рынок такого сложного изделия, как автомобиль, может произойти на один-два года раньше). При этом происходит значительная экономия средств, поскольку все аспекты внешнего вида оцениваются на компьютерных, а не натурных моделях. Дизайнерская часть общего цикла производства включает в себя: концептуальное моделирование, т.е. предварительную разработку нескольких вариантов изделия, в результате которой появляются "трехмерные наброски"; создание компьютерных "рисунков", представляющих собой ортогональные проекции будущего изделия (при традиционном дизайне - рисунки могли бы служить конечным результатом работы); собственно моделирование: трассировку рисунков, то есть создание с их помощью трехмерных объектов, а затем - построение поверхностей по этим объектам; оценку таких свойств моделируемых объектов, как кривизна, непрерывность кривизны, распределение бликов и т.д; задание "материалов" (т.е. оптических свойств поверхностей), выбор и расстановка источников света, задание свойств окружающей среды, выбор фона - все это заканчивается просчетом построенной таким образом сцены с высокой степенью фотореализма; передачу трехмерной модели объекта (вид которого наглядно представлен, оценен, согласован и утвержден) в САПР для дальнейшей разработки внутреннего устройства объекта, конструкторских расчетов, оформления чертежной документации и т.д.

Трехмерное моделирование - это область функционального пересечения дизайнерской системы и САПР, однако назначение моделирования в этих системах различается. Для дизайнера трехмерная модель - всего лишь предварительная конструкция, на основе которой получаются фотоизображения. При этом, нужно заметить, реально процесс разработки нового изделия происходит в режиме тесного сотрудничества конструкторов и технологов и содержит обратные связи, что позволяет еще на этапе дизайнерской разработки (а не при уже готовом изделии) довести модель "до ума", а это делает применение компьютерных технологий жизненно важным для будущего изделия. Таким образом, уже с самого начала формы будущего объекта согласуются с требованиями конструкторов и технологов. Созданный с помощью систем моделирования объект, можно помещать в различные среды, имитировать и прослеживать не только его перемещения в созданном для него виртуальном пространстве, но и демонстрировать его функционирование.

Если виртуальную реальность использовать просто как средство коммуникации между участниками процесса проектирования, она позволит проектировщикам, специалистам по надежности систем, персоналу и другим специалистам обсуждать, даже находясь в разных точках планеты, средствами Интернета, достоинства и недостатки проекта, используя виртуальную модель, как наглядное, трехмерное справочное пособие, которое можно как угодно перемещать в пространстве, "гулять" по нему и т.д. Это неизбежно приведет к более ясному пониманию сути проблем и более скорой выработке решений по устранению потенциальных затруднений во время проектирования и производства любого изделия.