16. Геометрический и энергетический смысл уравнения Бернулли.

Геометрический смысл уравнения Бернулли:

Положение любой частицы жидкости относительно некоторой произвольной линии нулевого уровня 0-0 определяется вертикальной координатой Z. Для реальных гидравлических систем это может быть уровень, ниже которого жидкость из данной гидросистемы вытечь не может. Например, уровень пола цеха для станка или уровень подвала дома для домашнего водопровода.

·  Величину Z называют нивелирной высотой.

·  Второе слагаемое -  носит название пьезометрическая высота. Эта величина соответствует высоте, на которую поднимется жидкость в пьезометре, если его установить в рассматриваемом сечении, под действием давления P.

·  Сумма первых двух членов уравнения 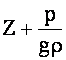  - гидростатический напор.

·  Третье слагаемое в уравнения Бернулли  называется скоростной высотой или скоростным напором. Данную величину можно представить как высоту, на которую поднимется жидкость, начавшая двигаться вертикально со скорость u при отсутствии сопротивления движению.

·  Сумму всех трёх членов (высот) называют гидродинамическим или полным напором и, как уже было сказано, обозначают буквой Н.

Все слагаемые уравнения Бернулли имеют размерность длины и их можно изобразить графически.

Значения 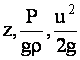  - нивелирную, пьезометрическую и скоростную высоты можно определить для каждого сечения элементарной струйки жидкости. Геометрическое место точек, высоты которых равны 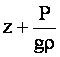, называется пьезометрической линией. Если к этим высотам добавить скоростные высоты, равные , то получится другая линия, которая называется гидродинамической или напорной линией.

Из уравнения Бернулли для струйки невязкой жидкости (и графика) следует, что гидродинамический напор по длине струйки постоянен.

Энергетический смысл уравнения Бернулли:

Энергию жидкости, отнесенную к единице массы, наз-т удельной энергией. Члены ур-ния Бернулли являются различными формами удельной энергии.

gz – удельная энергия положения, т.к. частица жидкости массой ∆m находясь на высоте z обладает потенциальной энергией, равной

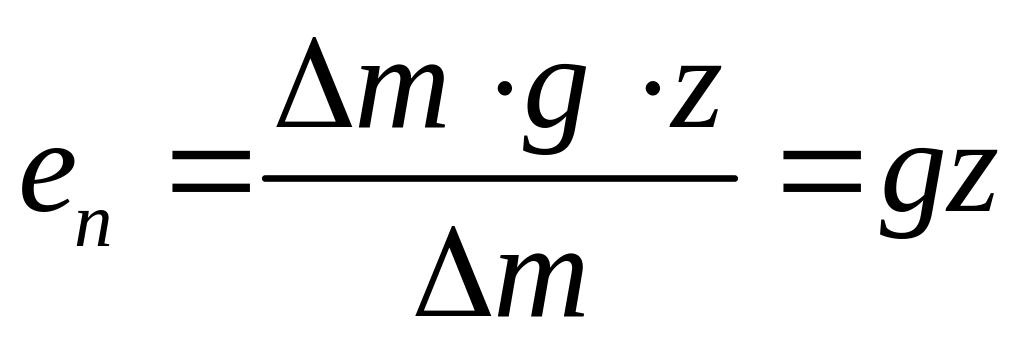
- удельная энергия давления, обладает способностью поднять жидкость на высоту

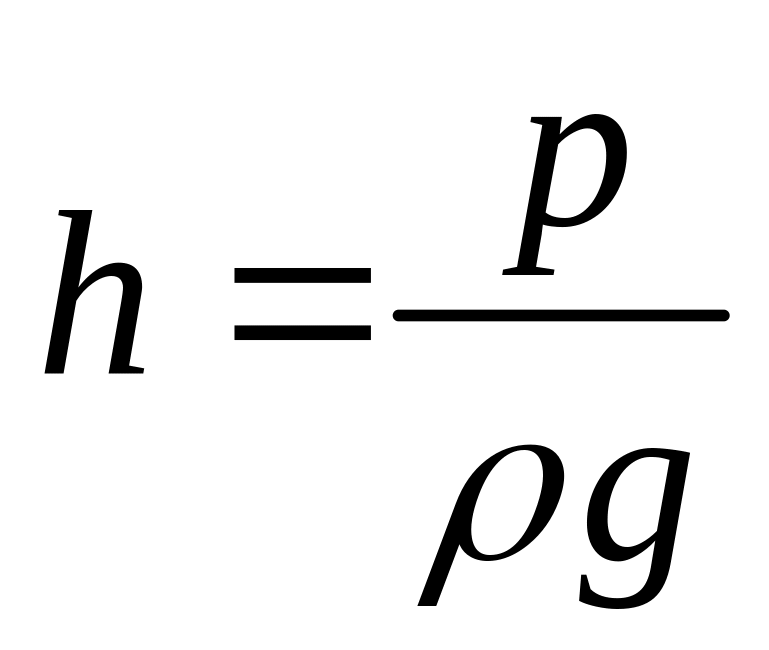и приобрести потенциальную энергию давления

На единицу массы приходится удельная энергия давления

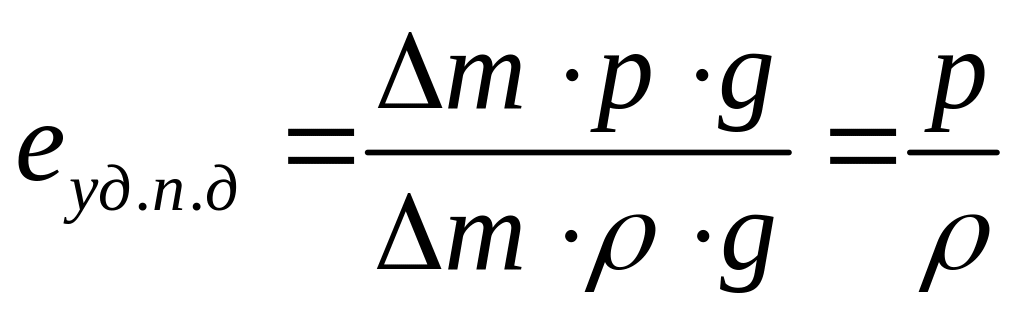
- удельная кинетическая энергия жидкости.

Т.к. ;

Полная удельная энергии частицы жидкости

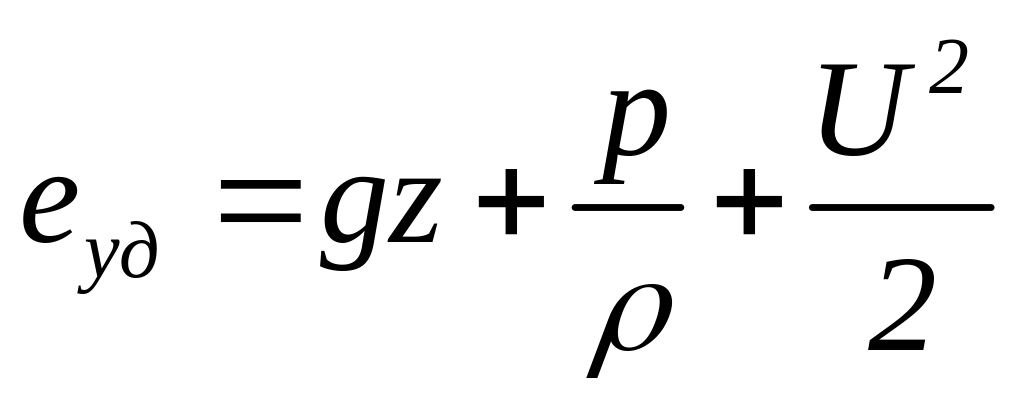
Следовательно энергитический смысл ур-ния Бернулли для элементарной струйки идеальной жидкости заключается в постоянстве вдоль струйки полной удельной энергии жидкости. Т.е. ур-ние Бернулли выражает собой закон сохранения мех. энергии в идеальной жидкости.

17. Уравнение Бернулли для потока реальной вязкой жидкости

.

Уравнение называется уравнением Д. Бернулли для потока жидкости и является основным уравнением гидродинамики; с его помощью получены многие расчетные формулы и решается ряд практических задач. Уравнение Бернулли устанавливает математическую связь между основными элементами движения жидкости, т. е. средней скоростью и гидродинамическим давлением.

Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения

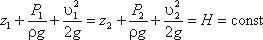
Дело в том, что при движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной энергии (рис.3.6).

Потерянная энергия или потерянный напор обозначаются и имеют также линейную размерность.

Уравнение Бернулли для реальной жидкости будет иметь вид:

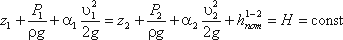
Из рис.3.6 видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1-1 и 2-2.

Кроме этого в уравнении появились еще два коэффициента α1 и α2, которые называются коэффициентами Кориолиса и зависят от режима течения жидкости ( α = 2 для ламинарного режима, α = 1 для турбулентного режима ).

Потерянная высота складывается из линейных потерь, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока)

= hлин + hмест

С помощью уравнения Бернулли решается большинство задач практической гидравлики. Для этого выбирают два сечения по длине потока, таким образом, чтобы для одного из них были известны величины Р, ρ, g, а для другого сечения одна или величины подлежали определению. При двух неизвестных для второго сечения используют уравнение постоянства расхода жидкости υ1ω 1 = υ2ω2.