14. Основные аналитические методы исследования движения жидкости.

Метод Лагранжа

Удобен для исследования движения мат. частицы твердого тела.

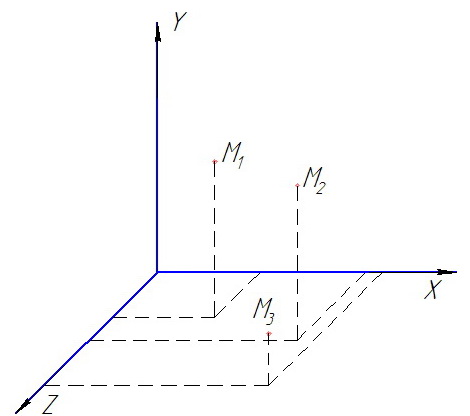
Будем считать, что для каждой частицы нам известны зависимости

Тогда, пользуясь ими, можно построить траектории намеченных частиц.

Далее в любой момент времени в любом месте этих траекторий можем найти длину пути, пройденного частицей за время dt. Зная путь и время можем найти скорость в данной точке, а также ускорение любой частицы жидкости в пространстве.

Согласно методу Лагранжа, о потоке жидкости вцелом судят по совокупному рассмотрению траекторий, описываемых частицами жидкости. X, Y, Z представляют собой текущие координаты частиц. Поэтому величины dx, dy, dz рассматриваются как проекции пути на соответствующие координаты.

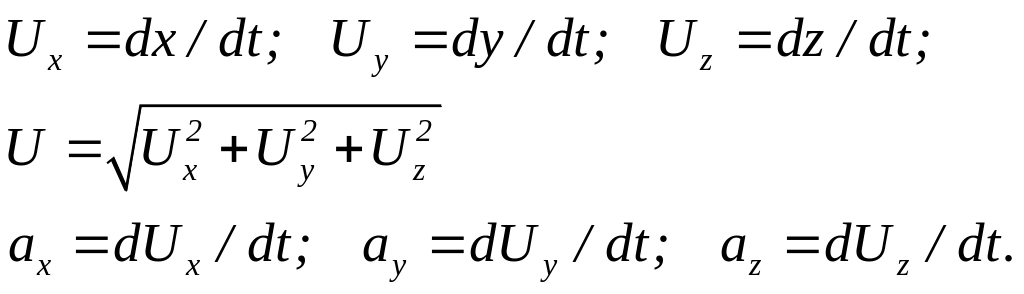
Метод Эйлера

Представим некоторую область, занятую движущейся жидкостью. Согласно Эйлера мы не следим за движением отдельных частиц жидкости и не интересуемся их траекториями. По этому методу в системе координат намечают неподвижные точки. Здесь x, y и z – координаты неподвижных точек в пространстве.

Р ассмотрим момент времени t. Поток представлен векторным полем скоростей, причем каждый вектор относится к определенной неподвижной точке и к данному моменту времени. В момент времени t₂ получаем другое поле скоростей.

При неустановившемся движении все поле скоростей изменяется во времени, следовательно компоненты скорости являются функциями не только координат, но и времени

Для установившегося движения поле скоростей остается неизменным во времени

При исследовании жидкости по методу Эйлера геом. характеристиками движения являются линии тока, а не траектории (метод Лагранжа).

Ур-ние линии тока можно составить, пользуясь следующими рассуждениями. Допустим в данный момент времени имеется плоская линия тока ab. Ур-ние этой линии ожжем записать y=f(x).

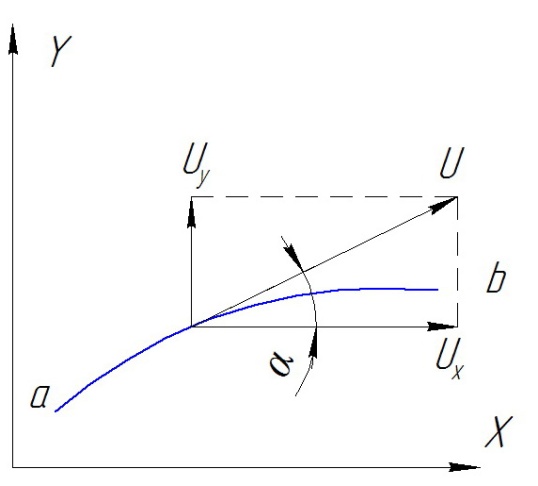
Дифференцируем его

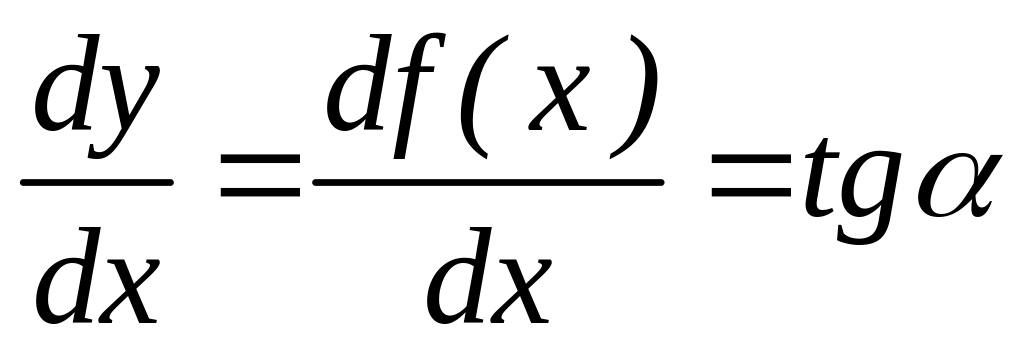- ДУ линии тока.

15. Уравнение Бернулли для элементарной струйки идеальной жидкости

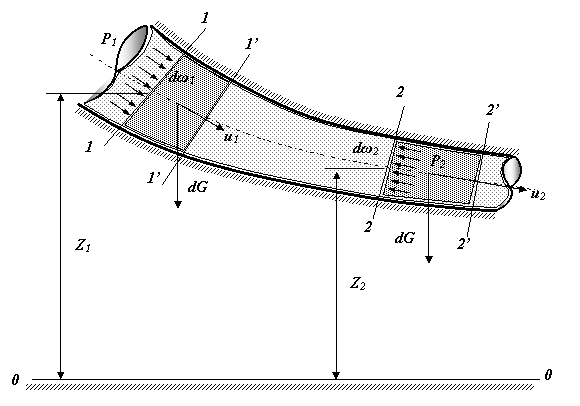
Рассмотрим элементарную струйку идеальной жидкости при установившемся движении, в которой выделим два сечения 1-1 и2-2.Площади живых сечений потока обозначим dω1 и dω2. Положение центров тяжести этих сечений относительно произвольно расположенной линии сравнения (нулевой линии) 0- 0 характеризуется величинами z1и z2. Давления и скорости жидкости в этих сечениях имеют значения P1, P2и u1, u2 соответственно.

Будем считать, что движение струйки жидкости происходит только под действием силы давления (внутреннее трение в жидкости отсутствует), а давление обладает свойствами статического и действует по нормали внутрь рассматриваемого объёма.

За малый промежуток времени dt частицы жидкости из 1-1 переместятся в 1'-1' на расстояние, равное u1dt, а частицы из 2-2 в 2' - 2' на расстояние u2dt.

Согласно теореме кинетической энергии приращение энергии тела (в данном случае выделенного объёма жидкости) равно сумме работ всех действующих на него сил.

Работу в данном случае производят силы давления, действующие в рассматриваемых живых сечениях струйки 1-1 и 2-2, а также силы тяжести. Тогда работа сил давления в сечении 1-1 будет положительна, т.к. направление силы совпадает с направлением скорости струйки. Она будет равна произведению силы p1dω1 на путь u1dt:

.

Работа сил давления в сечении 2-2 будет отрицательной, т.к. направление силы противоположно направлению скорости. Её значение

.

Полная работа, выполненная силами давления, примет вид:

.

Работа сил тяжести равна изменению потенциальной энергии положения выделенного объёма жидкости при перемещении из сечения 1-1 в сечение 2-2. С учётом условия неразрывности потока и несжимаемости жидкости выделенные элементарные объёмы будут равны и, следовательно, будут равны их веса dG:

.

путь за время dt.

элементарный объем.

Работа от сил давления

Приращение кинетической энергии

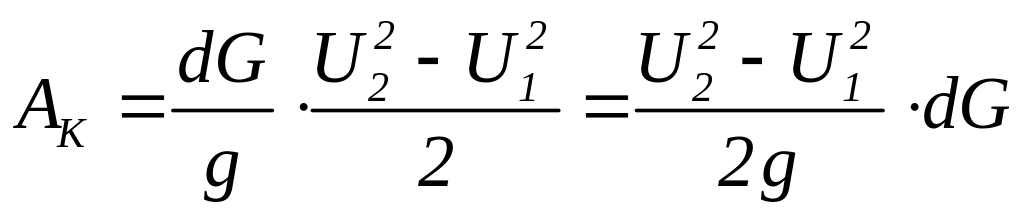
- ур-ние Бернулли.

·  Величину Z называют нивелирной высотой.

·  Второе слагаемое -  носит название пьезометрическая высота. Эта величина соответствует высоте, на которую поднимется жидкость в пьезометре, если его установить в рассматриваемом сечении, под действием давления P.

·  Третье слагаемое в уравнения Бернулли  называется скоростной высотой или скоростным напором. Данную величину можно представить как высоту, на которую поднимется жидкость, начавшая двигаться вертикально со скорость u при отсутствии сопротивления движению.

H – гидродинамический напор жидкости.