Основні формули

TR = P* Q	(9.1)
AR = TR/Q	(9.2)
MR = TR/Q	(9.3)
P = AR = MR	(9.4)
	(9.5)
	(9.6)
	(9.7)
Прибуток = ТR – ТС	(9.8)
Р=АТС або MR=P=MC=ATC	(9.9)
P = MR = LATC = LMC.	(9.10)

Основні формули

	(10.1)
	(10.2)

ПРИКЛАДИ

Завдання 1.  Нехай функція витрат монополіста має вигляд: ТС = 50 + Q² (тобто постійні витрати TFC становлять 50 грош. од., а змінні — Q²). Попит на продукцію монополіста задано як Р = 40 – Q.

Знайти, яку кількість товару буде виробляти монополіст, щоб максимізувати прибуток.

Розв’язання

Для визначення оптимального для монополіста обсягу виробниц­тва потрібно знайти середні та граничні витрати, сукупний і граничний виторг.

Середні витрати ;

Граничні витрати ;

Сукупний виторг монополіста ;

Граничний виторг .

Пам’ятаючи, що умовою максимізації прибутку монополіста є рівність граничного виторгу і граничних витрат (MC = MR),

одержимо 40 – 2Q = 2Q;

40 = 4Q;

Q = 10.

Отже, при обсязі в 10 од. прибуток монополіста максимальний. Для наочності зобразимо криві середнього і граничного виторгу, середніх і граничних витрат (рис. 11).

Криві MR i MC (рис. 11) перетинаються при Q = 10. При цьому величина середніх витрат становить 15 грош. од. за одиницю продукції

.

Ціна на продукцію — 30 грош. од. за одиницю, тому середній прибуток

30 – 15 = 15 (грош. од. за одиницю.)

Оскільки обсяг виробленої та реалізованої продукції 10 од., то прибуток фірми становить

15  10 = 150 (грош. од. — площа заштрихованого прямокутника).

 

Рис. 11. Середні та граничні витрати, середній та граничний виторг

Основні формули

	(11.1)
	(11.2)
або	(11.3)
;	(11.4)

ПРИКЛАДИ

Завдання 1.   Підприємство «Люба» виготовляє жіночі блузи (тис. од. на рік) і діє на ринку монополістичної конкуренції. Граничний виторг підприємства описується формулою МR = 20 – Q, а зростаючий відрізок кривої граничних витрат — формулою МС = 3Q – 10. Якщо мінімальне значення довгострокових середніх витрат (LAC) дорівнює 11 грош. од., то який буде надлишок виробничих потужностей у підприємства?

Розв’язання

Обсяг виробництва, що максимізує прибуток підприємства, задається умовою МR = MC. Звідси маємо оптимальний обсяг виробництва для умов монополістичної конкуренції:

20 – 2Q = 3Q – 10, Q_м.к. = 6.

Якби підприємство діяло на ринку досконалої конкуренції, то у довгостроковому періоді обсяг виробництва задавався би умовою Р = MR = = MC = LAC min. Тоді

3Q – 10 = 11,

звідси

Q_д.к. = 7.

Отже, недовантаження виробничих потужностей становить

Q_д.к. – Q_м.к. = 1 (тис. од. річного випуску).

Основні формули

,	(12.1)
...	(12.2)
...	(12.3)
	(12.4)
	(12.5)
	(12.6)
: , або	(12.7)
	(12.8)
	(12.9)
	(12.10)
	(12.11)
	(12.12)

: (12.13)

ПРИКЛАДИ

Завдання 1. Підприємство є монополістом на регіональному ринку праці й продає готову продукцію на конкурентному зовнішньому ринку.

Виробнича функція підприємства у короткостроковому періоді має такий вигляд:

Q_L = 300L – L²,

де Q — випуск, тис. шт.; L — обсяг праці, що використовується, тис. чол.

Функція пропозиції праці на регіональному ринку описується формулою:

L_S = 2W – 160.

Ціна готової продукції на зовнішньому ринку становить 0,5 грош. од. Визначте, яку кількість праці буде використовувати монопсонія, який рівень зарплати вона встановить, яку кількість продукції буде продавати на зовнішньому ринку та який виторг вона отримає?

Розв’язання

Функція граничного продукту у грошовому вираженні матиме вигляд (перша похідна від виробничої функції)

MP_L = 300 – 2L,

MRP_L = P_X (MP_L) = 150 – L.

Граничні витрати на працю становитимуть:

W = 80 = 0,5L,

TRC = 80L = 0,5L²,

MRC = 80 = L.

Прирівнюючи граничний продукт праці у грошовому вираженні до граничних витрат на працю, знайдемо оптимальну кількість робітників для монополії:

50 – L = 80 = L.

Оптимальна кількість робітників становить 35 тис. чол.

За допомогою функції пропозиції праці знайдемо рівень заробітної плати, який встановить монопсоніст, — 97,5 грош. од. Підставивши оптимальний обсяг використання робочої сили у формулу виробничої функції, отримаємо обсяг випуску — 9275 тис. од. Виторг монопсоніста дорівнює 4637,5 тис. грош. од.

ПРИКЛАДИ

Завдання 1. Обмежена кількість ресурсів (капіталу — 50 од.; праці — 100 од.) розподіляється між виробництвом товарів А та В. Виробництво товару А описується виробничою функцією Q_А = K^0,5L^0,5, а для виробництва товару В характерна функція Q_В = K^0,2L^0,8. Побудуйте (мінімум за трьома точками) криву виробничих контрактів.

Розв’язання

Нехай K₁ та K₂ — кількість капіталу, що використовується у виробництві, відповідно, товарів А та В, а L₁ та L₂ — кількість праці, що витрачається на виробництво, відповідно, товарів А та В.

Для Парето-оптимального розподілу ресурсів обов’язковою умовою є рівність між граничними нормами технологічного заміщення праці капіталом (відношення граничного продукту праці до граничного продукту капіталу) у виробництві А та у виробництві В. З цієї умови випливає:

0,5L₁/0,5K₁ = 0,8L₂/0,2K₂;

L₁/K₁ = 4(100 – L₁)/(50 – K₁);

K₁ = 50L₁ / (400 – 3L₁).

За останнім рівнянням визначимо координати трьох точок (M, T, N) на кривій виробничих контрактів і на кривій виробничих можливостей:

точка M: K₁ = 1,35; L₁ = 10; K₂ = 48,65; L₂ = 90;

точка T: K₁ = 10; L₁ = 50; K₂ = 40; L₂=50;

точка N: K₁ = 25; L₁ = 80; K₂ = 25; L₂ = 20.

Одержані дані дають змогу побудувати приблизний графік кривої виробничих контрактів (рис. 13):

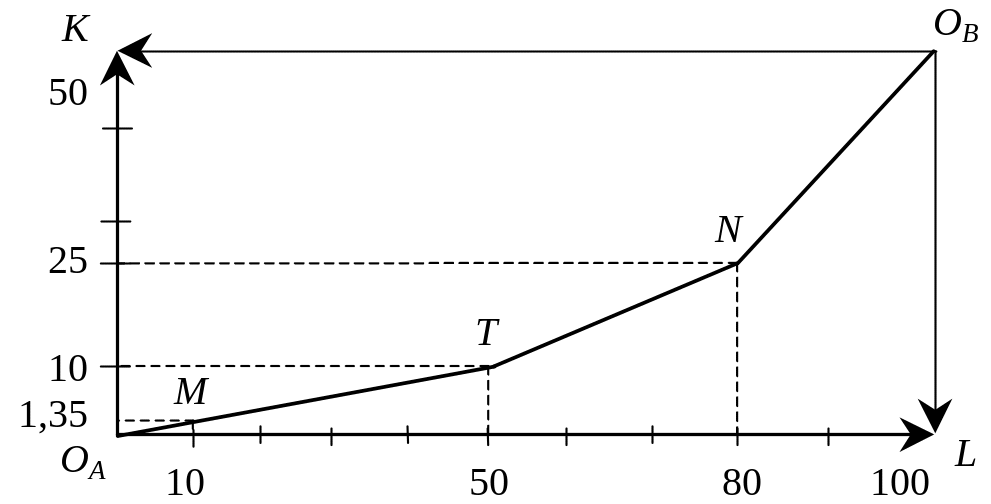
Рис. 13. Крива виробничих контрактів