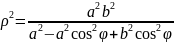- •Сложение матриц и умножение матрицы на число: определение и свойства, доказательство всех свойств.
- •Произведение матриц: определение и свойства, доказательство дистрибутивности.
- •Определение определителя произвольного порядка. Доказательство «правила треугольников» для определителя матрицы 3 X 3.
- •Приведение матрицы к упрощенному виду.
- •Перестановка двух строк.
- •Существование обратной матрицы.
- •Теорема о равенстве нулю миноров большого порядка.
- •Ранг матрицы и элементарные преобразования: формулировка теоремы, доказательство для прибавления к строке другой строки, умноженной на произвольное число.
- •Прибавление к строке другой строки, умноженной на произвольное число.
- •Единственность обратной матрицы. Обратная матрица к произведению. Матричныеуравнения.
- •Ранг матрицы и элементарные преобразования: формулировка теоремы, доказательство для перестановки строк и умножения строки на ненулевое число.
- •Перестановка строк.
- •Умножение строки на .
- •Формулы Крамера.
- •Лемма об элементарных преобразованиях матрицы системы. Метод Гаусса.
- •Теорема Кронекера-Капелли.
- •Теорема о количестве свободных переменных. Следствия из нее.
- •Скалярное произведение векторов: определение и свойства.
- •(Коммутативность).
- •Применения скалярного произведения: длина вектора, длина проекции одного вектора на другой, угол между векторами.
- •Длина вектора.
- •Длина проекции одного вектора на другой.
- •Угол между векторами.
- •Векторное произведение: определение и выражение через координаты сомножителей.
- •Смешанное произведение векторов: определение и геометрический смысл.
- •Векторное, параметрическое и каноническое уравнения прямой на плоскости.
- •Уравнение прямой на плоскости, проходящей через данные точки, и уравнение прямой в отрезках.
- •Общее и нормальное уравнения прямой на плоскости.
- •Угол между прямыми на плоскости.
- •Расстояние от точки до прямой, расстояние между параллельными прямыми на плоскости.
- •Общее и нормальное уравнение плоскости в пространстве.
- •Расстояние от точки до плоскости, расстояние между параллельными плоскостями.
- •Уравнение плоскости, проходящей через три данные точки, и уравнение плоскости в отрезках.
- •Векторное, параметрическое и каноническое уравнения прямой в пространстве.
- •Угол между прямыми в пространстве, угол между плоскостями, угол между прямой и плоскостью.
- •Каноническое уравнение эллипса.
- •Каноническое уравнение гиперболы.
- •Уравнение эллипса в полярных координатах, для случая, когда начало координат в центре эллипса.
- •Ранг матрицы и элементарные преобразования: формулировка теоремы, доказательство для прибавления к строке другой строки, умноженной на произвольное число.
- •Прибавление к строке другой строки, умноженной на произвольное число.
- •Ранг матрицы упрощенного вида.
Векторное, параметрическое и каноническое уравнения прямой в пространстве.
Векторное и параметрическое уравнения прямой в пространстве.
Пусть
 – направляющий вектор прямой
,
– направляющий вектор прямой
,
 – точка лежащая на
.
Тогда
можно записать уравнениями:
– точка лежащая на
.
Тогда
можно записать уравнениями:
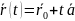 ,
где
- радиус вектор точки
;
,
где
- радиус вектор точки
; .
.
Доказательство.
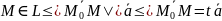 – для
некоторого числа t.
– для
некоторого числа t.

 ,
то
,
то
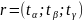
Каноническое уравнение прямой в пространстве.
Уравнение прямой можно записать в виде:
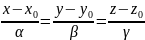 ,
если
,
если
 ;
; ,
если
,
если
 .
.
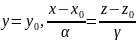 ,
если
,
если
 .
.
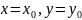 ,
если
,
если
 .
.
 ,
если
,
если
 .
.
 ,
если
,
если
 .
.
Доказательство.
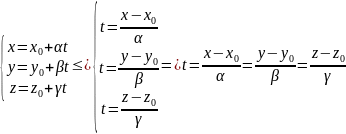
Пусть

Пусть

Угол между прямыми в пространстве, угол между плоскостями, угол между прямой и плоскостью.
У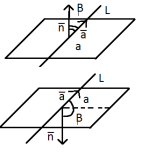 гол
между прямыми в пространстве.
гол
между прямыми в пространстве.
Пусть
 - это направляющие векторы прямых
- это направляющие векторы прямых
 .
Тогда:
.
Тогда:
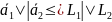 или
совпадают;
или
совпадают;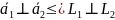 ;
; .
.
Угол между плоскостями.
Пусть
 - нормальные векторы плоскостей
- нормальные векторы плоскостей
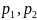 .
Тогда:
.
Тогда:
 или
совпадают;
или
совпадают; ;
; .
.
Угол между прямой и плоскостью.
Пусть направляющий вектор прямой , - нормальный вектор плоскости . Тогда:
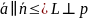
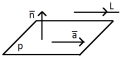 ;
; или
лежит в
;
или
лежит в
;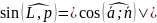

Доказательство.

![]()

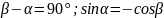

Каноническое уравнение эллипса.
Определение.Эллипсом называется множество точек плоскости, для каждой из которых сумма расстояний до двух данных точек – это постоянная величина большая, чем расстояние между данными точками.
Пусть
фокусы эллипса имеют координаты
 .
Тогда эллипс задается уравнением:
.
Тогда эллипс задается уравнением:
 ,
где
,
где
 .
.
Пример.
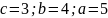
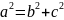
![]()


Доказательство.
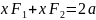
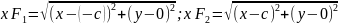
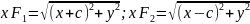





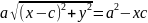


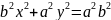
Гипербола y = k/x.
Определение. Гиперболой называется множество точек плоскости, для каждой из которых модуль разности расстояний до двух данных точек – постоянная величина меньшая, чем расстояние между данными точками.
Пусть
фокусы гиперболы
 и
и
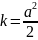 ,
тогда гипербола задается уравнением:
,
тогда гипербола задается уравнением:
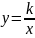
Пример.
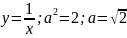

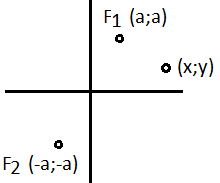
Доказательство.
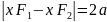
Рассмотрим случай.
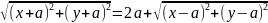



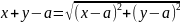


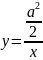
Каноническое уравнение гиперболы.
Пусть
фокусы гиперболы имеют координаты
.
Тогда гипербола задается уравнением
 ,
где
,
где
 .
.
Д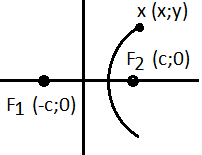 оказательство.
оказательство.
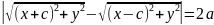
Рассмотрим случай.









Уравнение эллипса в полярных координатах, для случая, когда начало координат в центре эллипса.
Пусть
эллипс задан каноническим уравнением
,
 - эксцентриситет. Тогда в полярных
координатах эллипс задается уравнением
- эксцентриситет. Тогда в полярных
координатах эллипс задается уравнением
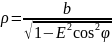
Эксцентриситет — числовая характеристика конического сечения, показывающая степень его отклонения от окружности.
Д![]() оказательство.
оказательство.

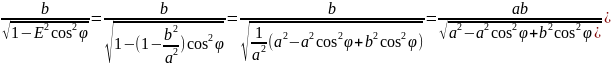
Проверим,
что уравнение эллипса – это