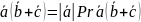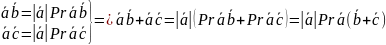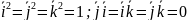- •Сложение матриц и умножение матрицы на число: определение и свойства, доказательство всех свойств.
- •Произведение матриц: определение и свойства, доказательство дистрибутивности.
- •Определение определителя произвольного порядка. Доказательство «правила треугольников» для определителя матрицы 3 X 3.
- •Приведение матрицы к упрощенному виду.
- •Перестановка двух строк.
- •Существование обратной матрицы.
- •Теорема о равенстве нулю миноров большого порядка.
- •Ранг матрицы и элементарные преобразования: формулировка теоремы, доказательство для прибавления к строке другой строки, умноженной на произвольное число.
- •Прибавление к строке другой строки, умноженной на произвольное число.
- •Единственность обратной матрицы. Обратная матрица к произведению. Матричныеуравнения.
- •Ранг матрицы и элементарные преобразования: формулировка теоремы, доказательство для перестановки строк и умножения строки на ненулевое число.
- •Перестановка строк.
- •Умножение строки на .
- •Формулы Крамера.
- •Лемма об элементарных преобразованиях матрицы системы. Метод Гаусса.
- •Теорема Кронекера-Капелли.
- •Теорема о количестве свободных переменных. Следствия из нее.
- •Скалярное произведение векторов: определение и свойства.
- •(Коммутативность).
- •Применения скалярного произведения: длина вектора, длина проекции одного вектора на другой, угол между векторами.
- •Длина вектора.
- •Длина проекции одного вектора на другой.
- •Угол между векторами.
- •Векторное произведение: определение и выражение через координаты сомножителей.
- •Смешанное произведение векторов: определение и геометрический смысл.
- •Векторное, параметрическое и каноническое уравнения прямой на плоскости.
- •Уравнение прямой на плоскости, проходящей через данные точки, и уравнение прямой в отрезках.
- •Общее и нормальное уравнения прямой на плоскости.
- •Угол между прямыми на плоскости.
- •Расстояние от точки до прямой, расстояние между параллельными прямыми на плоскости.
- •Общее и нормальное уравнение плоскости в пространстве.
- •Расстояние от точки до плоскости, расстояние между параллельными плоскостями.
- •Уравнение плоскости, проходящей через три данные точки, и уравнение плоскости в отрезках.
- •Векторное, параметрическое и каноническое уравнения прямой в пространстве.
- •Угол между прямыми в пространстве, угол между плоскостями, угол между прямой и плоскостью.
- •Каноническое уравнение эллипса.
- •Каноническое уравнение гиперболы.
- •Уравнение эллипса в полярных координатах, для случая, когда начало координат в центре эллипса.
- •Ранг матрицы и элементарные преобразования: формулировка теоремы, доказательство для прибавления к строке другой строки, умноженной на произвольное число.
- •Прибавление к строке другой строки, умноженной на произвольное число.
- •Ранг матрицы упрощенного вида.
Теорема Кронекера-Капелли.
Теорема.
Система уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы.
Доказательство.
Приведем матрицу систему к упрощенному виду преобразованиями 1) 2) 3) со строками расширенной матрицы и 1’,2’ со столбцами матрицы системы.
По теореме о ранге и элементарном преобразовании ранги матрицы системы и расширенной матрицы системы не изменились.
По лемме об элементарном преобразовании матрицы системы: совместная матрица => в совместную; несовместная матрица => в несовместную.
Случай 1.
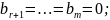 система
совместна.
система
совместна.
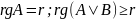 ,
по теореме о ранге матрицы упрощенного
вида.
,
по теореме о ранге матрицы упрощенного
вида.
Случай 2.
Не
все числа
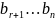 равны 0.
равны 0.
Пусть
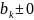 ;
система
несовместна.
;
система
несовместна.
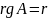 ,
по теореме о ранге матрицы упрощенного
вида.
,
по теореме о ранге матрицы упрощенного
вида.
Докажем,
что
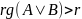 ,
т.е. что
есть ненулевой минор порядка
,
т.е. что
есть ненулевой минор порядка
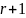 .
.
Минор:
строки
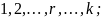 столбца:
столбца:
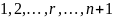 .
.

Разложим по последней строке.
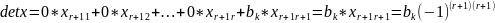
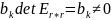 =>x
– ненулевой
минор порядка
=>
=>x
– ненулевой
минор порядка
=>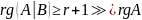 =>
=>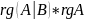
Теорема о количестве свободных переменных. Следствия из нее.
Теорема.
Дана система линейных уравнений с n неизвестных. Предположим, что система совместна. Пусть r – ранг матрицы системы.
Если
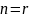 ,
то система – определенная.
,
то система – определенная.Если
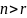 ,
то система – неопределенная. Имеет
бесконечно много решений.
,
то система – неопределенная. Имеет
бесконечно много решений.
Можно
выбрать
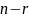 переменных так, что при любых их значениях
остальные r
переменные определяются однозначно.
(т.е. есть
свободных переменных).
переменных так, что при любых их значениях
остальные r
переменные определяются однозначно.
(т.е. есть
свободных переменных).
Доказательство.
Приведем матрицу систему к упрощенному виду. Преобразовав 1, 2, 3 со строками расширенной матрицы и 1’ со столбцами матрицы системы.
По лемме об элементарных преобразованиях матрицы системы, количество свободных переменных не изменяется.
По
теореме о ранге и элементарных
преобразованиях
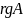 не изменяется.
не изменяется.
Следствие 1.
Система линейных уравнений может иметь 0, 1 или бесконечно много решений.
Доказательство.
Несовместна – 0 решений.
Совместна – по доказательству теоремы либо определенная (1 решение, не свободных переменных), либо есть свободная переменная => бесконечна.
Следствие 2.
Если количество уравнений меньше, чем количество неизвестных, то система либо несовместная, либо неопределенная.
Доказательство.
Пусть
m
уравнений, n
неизвестно
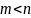 .
.
Предположим, что система совместная.
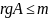 ,
(размер минора не больше, чем количество
строк) =>
,
(размер минора не больше, чем количество
строк) =>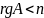 => система неопределенная.
=> система неопределенная.
Следствие 3.
Дана система из n линейных уравнений с n неизвестными. Пусть A – матрица сиcтема,
Если r=n, то система определенная. (при любых свободных членах).
Если r<n, то система либо несовместная, либо неопределенная.
Скалярное произведение векторов: определение и свойства.
Определение.
Скалярное
произведение вектора
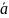 и
и
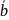 называется число
называется число
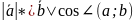 .
.
Свойства.
(Коммутативность).
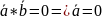 или
или
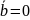 или
или
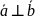 .
.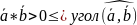 острый
или равен 0.
острый
или равен 0.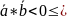 угол
угол
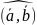 тупой (90) или развернутый (180).
тупой (90) или развернутый (180).
Доказательство.
Пусть
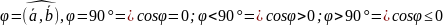 .
.
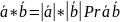 (проэкция).
(проэкция).
Доказательство.
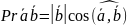 (свойство
Pr)
(свойство
Pr)
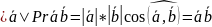
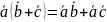 (дистрибутивность).
(дистрибутивность).