9. Ранг матрицы и элементарные преобразования: формулировка теоремы, доказательство для перестановки строк и умножения строки на ненулевое число.

Теорема.

При элементарных преобразованиях ранг матрицы не меняется.

Доказательство.

Пусть B полученную из A элементарным преобразованием.

Проверим, что .

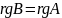Можно считать, что B полученную из A одним преобразованием.

Докажем, что .

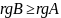Пусть ; Проверим, что .

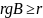У A есть не нулевой минор порядка r.

Проверим, что у B есть не нулевой минор порядка r.

Пусть X – не нулевой минор матрицы A порядка r.

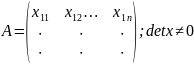
2. Перестановка строк.

• Переставим строки, не входящие в x =>x-не изменяется.

• Переставим строки, входящие в х => .

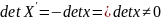
• Переставим строку, входящую в x, а строку не входящую в x =>

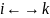
i – входит в x.

k – не входит в x.

Рассмотрим минор x’ матрицы B, полученную из X заменой i строки на k строку.

x’- полученную из x перестановками строк.

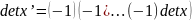(свойство 3)

3. Умножение строки на .

• Строка не входящая в x =>x не изменяется.

• Строка входящая в x

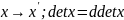(свойство 4); .

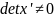12. Формулы Крамера.

Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы.

Теорема.

1. Если матричная система квадратная и невыраженная, то система совместная и определенная.

2. Пусть ( 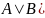расширенная матричная система, - вектор столбца, тогда .

3. Пусть

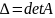
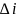–определитель матрицы, полученный из A заменой I столбца на B. Тогда .

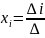Доказательство.

1)2) Из теоремы о матричном упрощении.

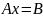, имеет единственное решение

Пусть – матрица полученная из матрицы заменой.

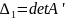
Разложим 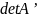по i столбцу.

Найдем x из равенства

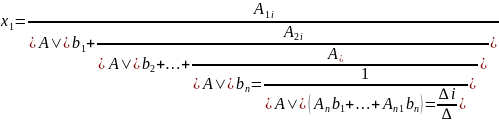
12. Лемма об элементарных преобразованиях матрицы системы. Метод Гаусса.

Лемма об элементарных преобразованиях матрицы системы.

Пусть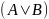 – расширенная матрица система. Тогда:

1. При элементарных преобразованияхсо строками матрицы системы переходит в равносильную.

2. Элементарное преобразование 1’) матрицы соответствует перенумерации переменных.

3. При элементарных преобразованиях 1) 2) 3) матрицы и элементарном преобразовании 1’) матрицы , из совместной => совместную; из несовместной => несовместную; из определенной =>определенную; из неопределенной => неопределенную.

Доказательство.

1. Система с рациональной матрицей .

Пустьиз (*) получена система (**).

Докажем, что если – решение системы (*), то – решение системы (**).

1. Перестановка уравнений.

2. Умножение строки на ненулевое число .

Если 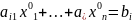верно, то и 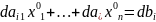тоже верно.

Эти две части умножим на .

Преобразование 3. Прибавим к строке строку умноженную на .

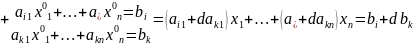
Докажем, что любое решение второй матрицы является решением первой матрицы.

По лемме обобратных элементарных преобразований, то систему (**) можно получить из системы (*) преобразованиями такого же типа.

Любое решение первой системы является решением второй системы.

2. Поменяем и столбец.

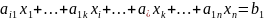
Поменяли местами коэффициенты 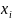и .

3. Следует из 1 и 2.

Метод Гаусса.

Нужно привести матрицу системы к упрощенному виду преобразованиями 1) 2) 3) 1’).Преобразования 1) 2) 3) нужно делать с расширенной матрицей.

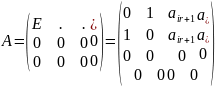
Получим систему:

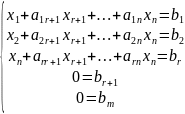
Если хотя бы одно из чисел 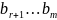не равно 0, то решений нет, система несовместна.

Если 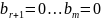,то система совместна и ее общее решение:

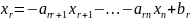
- свободные переменные.

Если 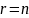, то свободных переменных нет.