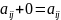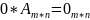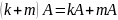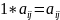- •Сложение матриц и умножение матрицы на число: определение и свойства, доказательство всех свойств.
- •Произведение матриц: определение и свойства, доказательство дистрибутивности.
- •Определение определителя произвольного порядка. Доказательство «правила треугольников» для определителя матрицы 3 X 3.
- •Приведение матрицы к упрощенному виду.
- •Перестановка двух строк.
- •Существование обратной матрицы.
- •Теорема о равенстве нулю миноров большого порядка.
- •Ранг матрицы и элементарные преобразования: формулировка теоремы, доказательство для прибавления к строке другой строки, умноженной на произвольное число.
- •Прибавление к строке другой строки, умноженной на произвольное число.
- •Единственность обратной матрицы. Обратная матрица к произведению. Матричныеуравнения.
- •Ранг матрицы и элементарные преобразования: формулировка теоремы, доказательство для перестановки строк и умножения строки на ненулевое число.
- •Перестановка строк.
- •Умножение строки на .
- •Формулы Крамера.
- •Лемма об элементарных преобразованиях матрицы системы. Метод Гаусса.
- •Теорема Кронекера-Капелли.
- •Теорема о количестве свободных переменных. Следствия из нее.
- •Скалярное произведение векторов: определение и свойства.
- •(Коммутативность).
- •Применения скалярного произведения: длина вектора, длина проекции одного вектора на другой, угол между векторами.
- •Длина вектора.
- •Длина проекции одного вектора на другой.
- •Угол между векторами.
- •Векторное произведение: определение и выражение через координаты сомножителей.
- •Смешанное произведение векторов: определение и геометрический смысл.
- •Векторное, параметрическое и каноническое уравнения прямой на плоскости.
- •Уравнение прямой на плоскости, проходящей через данные точки, и уравнение прямой в отрезках.
- •Общее и нормальное уравнения прямой на плоскости.
- •Угол между прямыми на плоскости.
- •Расстояние от точки до прямой, расстояние между параллельными прямыми на плоскости.
- •Общее и нормальное уравнение плоскости в пространстве.
- •Расстояние от точки до плоскости, расстояние между параллельными плоскостями.
- •Уравнение плоскости, проходящей через три данные точки, и уравнение плоскости в отрезках.
- •Векторное, параметрическое и каноническое уравнения прямой в пространстве.
- •Угол между прямыми в пространстве, угол между плоскостями, угол между прямой и плоскостью.
- •Каноническое уравнение эллипса.
- •Каноническое уравнение гиперболы.
- •Уравнение эллипса в полярных координатах, для случая, когда начало координат в центре эллипса.
- •Ранг матрицы и элементарные преобразования: формулировка теоремы, доказательство для прибавления к строке другой строки, умноженной на произвольное число.
- •Прибавление к строке другой строки, умноженной на произвольное число.
- •Ранг матрицы упрощенного вида.
Сложение матриц и умножение матрицы на число: определение и свойства, доказательство всех свойств.
Сложение.
Определено
для матриц одинакового размера
 .
.
Сумма.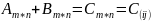 ,
где
,
где
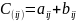
Пример.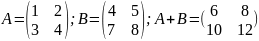
Противоположная матрица к матрице
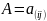 -
это
матрица
-
это
матрица
Пример.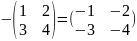
Разность.

Пример.
Свойства.
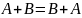 (коммутативность)
(коммутативность) (ассоциативность)
(ассоциативность)

Доказательство.
Пусть
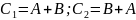
Элементы

Для
любых чисел
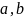 верно
верно
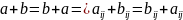 ;
для любых
;
для любых
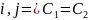
Умножение.
Умножение
матрицы на число
 ,
K-число;
K*
,
K-число;
K* – это
– это
 ,
где
,
где
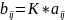
Пример.
Свойства.
Доказательство.
Пример.

Произведение матриц: определение и свойства, доказательство дистрибутивности.
Произведение матриц.
Определено, если число столбцов первой матрицы равно числу строк второй матрицы. (Длина строки первой матрицы равна высоте столбцов второй матрицы)
Произведение.
 ,
где
,
где
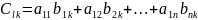

Свойства.
Доказательство дистрибутивности.

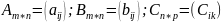
Рассмотрим элементы на месте i, k.

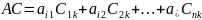
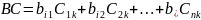

Определение определителя произвольного порядка. Доказательство «правила треугольников» для определителя матрицы 3 X 3.
Определитель - одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно).
Правило треугольника. (для 3 х 3).
П![]() усть
усть
 ,
тогда
,
тогда
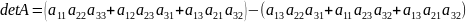
Доказательство.
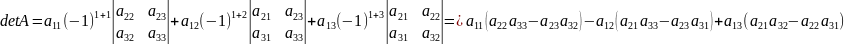
Свойства определителя: формулировка всех свойств, доказательство свойств про перестановку двух строк, про матрицу с двумя одинаковыми строками, и про умножение на алгебраические дополнения другой строки.
Свойства определителя.
 .
. .
.Перестановка двух столбцов или двух строк определителя равносильна умножению его на (-1).
Пример.

Если определитель имеет два одинаковых столбца или две одинаковые строки, то
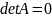 .
.Если матрица содержит нулевую строку (столбец), то определитель этой матрицы равен нулю.
Умножение всех элементов строки или столбца определителя на некоторое число d равносильно умножению определителя на это число.
Определитель не изменится, если к элементам любой его строки (или столбца) прибавить соответствующие элементы другой строки (или соответствующего столбца), умноженные на одно и тоже число.
Пусть A и B – квадратные матрицы одного и того же порядка. Тогда определитель произведения матриц равен произведению определителей.
Доказательство.
Перестановка двух строк.
Индукция
по
 .
.
База

Переход
от n-1
к n.
(Если свойство верно для матриц
 ,
то верно и для матриц
.
,
то верно и для матриц
.
 .
Переставляем i
и k
строки.
.
Переставляем i
и k
строки.
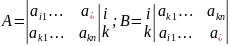
 – такое
число, что
– такое
число, что
Разложим по L строке.
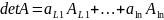
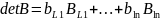
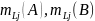 – определитель
матриц
.
– определитель
матриц
.
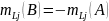

Матрица с двумя одинаковыми строками.

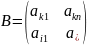 ,
переставим
i
и k.
,
переставим
i
и k.
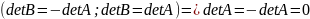
Умножение на алгебраические дополнения другой строки.

Пусть

Разложим
 по k
строке A.
(свойство 2)
по k
строке A.
(свойство 2)




(По
свойству
4)