МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Н.М. Захаров, Р.Р. Газиев

Филиал УГНТУ в г. Салавате

Кафедра “Оборудование предприятий нефтехимии и нефтепереработки”

прикладнАЯ механика

Учебно-методическое пособие для бакалавров по выполнению расчетно-проектировочной работы

Уфа

2011

Учебно-методическое пособие предназначено для бакалавров всех форм обучения направления 240100 “Химическая технология” профиля “Химическая технология природных энергоносителей и углеродных материалов”. В пособии приведены варианты заданий и примеры решения задач расчетно-проектировочной работы по дисциплине “Прикладная механика”.

Составители: Захаров Н.М., доц., канд. техн. наук

Газиев Р.Р., доц., канд. техн. наук

Рецензенты: Муртазин Ф. Р., доц., канд. техн. наук

Трутнев Р.Н., зам.главного конструктора

ОАО “Салаватнефтемаш”, канд. техн. наук

© Уфимский государственный нефтяной технический университет, 2011

Общие требования по выполнению и оформлению расчетно-проектировочных работ

1 Вариант задания и перечень задач расчетно-проектировочной работы (РПР) выдаются преподавателем.

2 Перед выполнением РПР следует изучить теоретический материал соответствующего раздела курса и приобрести необходимые навыки решения задач и их оформления в соответствии с нормативными документами.

3 Каждая РПР оформляется согласно ГОСТ 2.105-95 ЕСКД. “Общие требования к текстовым документам” черными чернилами, пастой или тушью, рукописным, машинописным текстом или на ЭВМ. РПР состоит из пояснительной записки с титульным листом и графической части.

3.1 Каждая задача РПР начинается с новой страницы, на которой указывается номер и название задачи, задание и порядок решения, исходные данные и заданная исходная схема (согласно варианту).

3.2 На последующих страницах выполняется решение задачи, основные этапы которого сопровождаются краткими пояснениями с указанием использованных библиографических источников, расчетными схемами, рисунками, эскизами и таблицами.

3.3 Расчетная схема и основные результаты решения представляются в графической форме на отдельной странице, которая может быть размещена после задания или в конце пояснительной записки (может быть увеличенного формата в виде приложения). Эпюры внутренних силовых факторов, напряжений и перемещений изображаются строго под расчетной схемой на той же странице.

3.4 Каждый этап решения задач выполняется в аналитической форме. Числовые значения подставляются только в окончательные выражения в основных единицах системы СИ с соблюдением правил ведения технических записей (см. решения примеров).

3.5 При повторном представлении РПР на проверку после исправления указанных замечаний следует сохранять все листы с пометками преподавателя.

1 Эпюры внутренних силовых факторов

1.1 Внутренние силы. Метод сечений. Внутренние силовые факторы

Внутренними называются силы, возникшие между элементарными частями тела (к ним относятся кристаллы, молекулы, атомы), сохраняющие тело как единое целое. При внешнем воздействии на любое тело внутренние силы в нем изменяются и появляются дополнительные составляющие, называемые внутренними силами упругости или внутренними усилиями (В.У.). Благодаря этим внутренним усилиям тело пытается вернуться в исходное положение при снятии внешней нагрузки. Если же в нагруженном теле внутреннее усилие достигает своего предельного значения, происходит разрушение.

В курсе сопротивления материалов часто приходится определять внутренние усилия, характеризующие прочность проектируемых конструкций. С этой целью применяется так называемый метод сечений (М.С.). Суть метода сечений заключается в следующем.

Тело, нагруженное системой уравновешенных нагрузок, рассекается в месте, где необходимо найти внутренние усилия (рисунок 1.1).

Отделяется одна из частей тела, а ее действие заменяется внутренними усилиями, действующими в поперечном сечении этого тела (рисунок 1.2).

Внутренние усилия в сечении тела приводятся к главному вектору и главному моменту (рисунок 1.3).

Главный вектор и главный момент проецируются на три главные центральные оси координат (рисунок 1.4). В итоге получают шесть компонентов внутренних усилий, называемых внутренними силовыми факторами (ВСФ).

Внутренние силовые факторы имеют следующие наименования: N_z - продольная (или нормальная) сила; Q_x, Q_y - поперечные силы; M_z - крутящий момент; M_x, M_y - изгибающие моменты. При известных внешних силах все шесть ВСФ определяются из шести уравнений равновесия, которые составляются для отсеченной части бруса в таком виде:

На основе этих уравнений можно сформулировать правила для определения величин каждого внутреннего силового фактора.

Продольная сила N_z в любом сечении численно равняется алгебраической сумме проекций на продольную ось бруса всех внешних сил, расположенных по одну сторону от рассматриваемого сечения.

Поперечные силы Q_x, Q_y в любом сечении равняются алгебраическим суммам проекций на нормали Х и Y к оси бруса всех внешних сил, распложенных по одну сторону от рассматриваемого сечения.

Крутящий момент M_z в любом сечении равняется алгебраической сумме моментов относительно продольной оси бруса всех внешний сил, расположенных по одну сторону от сечения.

Изгибающие моменты M_x, M_y в любом сечении равняются алгебраической сумме моментов относительно оси Х или соответственно относительно оси Y всех внешних сил, расположенных по одну сторону от рассматриваемого сечения.

Каждый из ВСФ связывают с определенным видом деформации бруса. Так, продольная сила возникает при деформации растяжения или сжатия, поперечная сила – при сдвиге или срезе, крутящий момент – при кручении и изгибающий момент – при изгибе.

Рассмотренный выше метод сечений позволяет найти любой ВСФ в произвольном месте нагруженного бруса. Для этого удобно воспользоваться так называемым правилом РОЗУ:

- Рассекаем брус в рассматриваемом сечении.

- Отбрасываем одну из частей (любую).

- Заменяем действие отброшенной части искомым ВСФ.

- Уравновешиваем оставшуюся часть бруса, т. е. составляем уравнения равновесия, из которых находим величины ВСФ.

1.2 Эпюры внутренних силовых факторов и их построение

В различных сечениях одного и того же бруса внутренние силовые факторы различны. Для расчета конструкций на прочность весьма важно знать как величину внутренних силовых факторов, так и характер их изменения по длине бруса, что устанавливается по эпюрам ВСФ.

Эпюрой называется график, характеризующий закон изменения какого-либо параметра (например, ВСФ, напряжения, перемещения, температуры и др.) по длине или высоте составной части конструкции. Эпюра позволяет установить местоположение опасного сечения, где вероятнее всего произойдет разрушение конструкции.

При построении эпюр необходимо придерживаться следующих общих правил и порядка.

Правила построения эпюр ВСФ:

- ось, или база, эпюры выбирается рядом с исходной расчетной схемой;

- ординаты эпюры откладываются от оси в масштабе с учетом знака;

- поле эпюры подвергается штриховке (штриховые линии должны быть перпендикулярны к оси эпюры), внутри него указывается знак и обозначаются характерные ординаты эпюры;

- выше или рядом с эпюрой дается ее название и указывается размерность, если эпюра построена в числовом виде.

Порядок построения эпюр ВСФ:

- расчетная схема заданного бруса разбивается на силовые участки, то есть участки, в пределах которых закон изменения заданного фактора является одним и тем же, т.е. неизменным. Границами силовых участков являются сечения, в пределах которых действуют внешние нагрузки (M, F, q) или изменяются направление оси и поперечные размеры бруса;

- для каждого силового участка применяется метод сечений (правило РОЗУ) и составляется общее уравнение искомого ВСФ в виде функции переменной абсциссы z;

- по этим уравнениям определяются характерные ординаты и выполняется построение эпюры в соответствии с вышерассмотренными правилами (рисунок 1.5).

При построении эпюр ВСФ предварительно устанавливаются правила знаков, которые являются условными для каждого ВСФ. В дальнейшем будем принимать следующие правила знаков.

Правило знаков для продольной силы N. Продольная сила считается положительной, если внешняя продольная нагрузка вызывает растяжение бруса по отношению к выбранному сечению, и продольная сила отрицательна, если  вызывает сжатие бруса (рисунок 1.6).

Правило знаков для крутящего момента M_кр.. Крутящий момент считается положительным, если при взгляде со стороны сечения на оставшуюся часть бруса момент внешних нагрузок (вращающий момент) направлен против часовой стрелки, и крутящий момент отрицателен, если по часовой стрелке (рисунок 1.7).

П равило знаков для поперечной силы Q. Поперечная сила считается положительной, если внешняя поперечная нагрузка пытается повернуть оставшийся участок бруса по часовой стрелке относительно сечения, и отрицательной, если против часовой стрелки (рисунок 1.8).

П равило знаков для изгибающего момента М_изг.. Изгибающий момент считается положительным, если относительно сечения внешние нагрузки действуют таким образом, что нижние волокна (слои) бруса растянуты, а верхние волокна (слои) сжаты, и изгибающий момент отрицателен, если все наоборот (рисунок 1.9).

При построении эпюры изгибающих моментов можно использовать один из следующих приемов откладывания ординат от оси эпюры:

-на растянутом волокне – означает, что эпюра строится с той стороны бруса, с которой ее волокна растянуты (в этом случае для балок знак «+» оказывается снизу, а знак «–» – сверху);

- на сжатом волокне – означает, что эпюра строится с той стороны балки, с которой ее волокна сжаты (в этом случае знак «+» оказывается сверху, а знак «–» – снизу).

П ример построения эпюры моментов на растянутом и сжатом волокне показан на рисунке 1.10.

1.3 Дифференциальные зависимости между поперечной силой и изгибающим моментом. Пункты контроля правильности построения эпюр внутренних силовых факторов

Рассмотрим брус, нагруженный произвольной распределенной нагрузкой (рисунок 1.11, а). Двумя сечениями I-I и II-II вырежем из бруса бесконечно малый участок длиной dz. В этом случае действующую внешнюю нагрузку можно считать равномерно распределенной, или постоянной (рисунок 1.11, б).

Составляем уравнения равновесия для этого бесконечно малого участка бруса. Сумма проекций всех внешних и внутренних сил на вертикальную ось равна

_{откуда (1.2)}

Рисунок 1.11 – Брус, нагруженный распределенной нагрузкой (а), и его

бесконечно малый участок (б)

Сумма моментов всех сил относительно сечения II – II:

(1.3)

откуда получим

(1.4)

Подставим (1.4) в (1.2), получим

(1.5)

Система уравнений (1.2), (1.4) и (5.5) носит название дифференциальных зависимостей при изгибе. Основываясь на этих зависимостях, можно выполнить проверку правильности построения эпюр ВСФ.

Рассмотрим основные пункты контроля правильности построения эпюр ВСФ для случая изгиба:

1 На участках, где действует только внешний момент, эпюра Q отсутствует, а эпюра M ограничена прямой, параллельной оси эпюры (рисунок 1.12).

2 На участках, где действует только сила, эпюра Q ограничена прямой, параллельной оси, а эпюра M – наклонной линией (рисунок 1.13).

3 На участках, где действует только равномерно распределенная нагрузка, эпюра Q ограничена наклонной, а эпюра M – параболой, причем кривизна параболы совпадает с направлением стрелок распределенной нагрузки. Это утверждение справедливо только для растянутого волокна (рисунок 1.14).

4 В сечениях, где приложен внешний момент, эпюра Q остается неизменной, а на эпюре M наблюдаются «скачки» на величину внешнего момента (рисунок 1.15).

5 В сечениях, где приложена внешняя сила, на эпюре Q наблюдается «скачок» по направлению и величине внешней силы, а на эпюре M возникает излом линии, острие которого (излома) совпадает с направлением внешней силы, если эпюра построена на растянутом волокне (рисунок 1.16).

6 В сечениях, где эпюра Q пересекает осевую линию, а ее ордината равна нулю, на эпюре M имеет место экстремальный момент, т. е. максимальный или минимальный в пределах данного участка (рисунок 1.17).

7 На участках, где Q больше нуля, ординаты эпюры M слева направо алгебраически возрастают, а где Q меньше нуля – убывают (рисунки 1.13 – 1.17).

8 Ординаты эпюры Q изменяются прямо пропорционально тангенсу угла наклона касательной к эпюре моментов в данной точке (рисунок 1.18), т.е.

2 Растяжение и сжатие

Центральным растяжением или сжатием называется такой вид деформации, при котором в сечении бруса, называемого стержнем, возникает только один внутренний силовой фактор – продольная сила N_z (рисунок 2.1).

При растяжении-сжатии в поперечных сечениях стержня возникают как нормальные . Рассмотрим их более подробно.

2.1 Напряжения в поперечных сечениях стержня

Получим зависимость для нормального напряжения, которое возникает в поперечных сечениях стержня. Для этого рассмотрим следующие стороны задачи о растяжении стержня с постоянной площадью поперечного сечения А.

Статическая сторона задачи. Используем интегральное уравнение равновесия, связывающее между собой продольную силу N_z и нормальное напряжение _z, возникающее в поперечном сечении стержня

Чтобы из данного уравнения получить зависимость для нахождения нормального напряжения _z, необходимо провести анализ напряженно-деформированного состояния стержня, т.е. установить закон изменения деформаций и напряжений в поперечном сечении стержня.

Геометрическая сторона задачи. Нанесем на поверхность стержня перпендикулярно к продольной оси сетку с постоянным шагом. После нагружения бруса можно видеть, что линии сетки перемещаются с одинаковым приращением параллельно самим себе, оставаясь прямыми и перпендикулярными к оси стержня (рисунок 2.2). Анализ деформации стержня показывает, что при растяжении-сжатии является справедливой гипотеза плоских сечений (гипотеза Бернулли): поперечные сечения стержня, плоские до деформации, остаются плоскими и после деформации, перемещаясь поступательно вдоль его продольной оси.

На основании этого можно считать, что продольные волокна стержня удлиняются на одну и ту же величину. Следовательно, в поперечных сечениях стержня продольные деформации и нормальные напряжения распределяются равномерно, т.е. по постоянному закону.

Таким образом, видим, что

Преобразуем (2.1) с учетом (2.2), имеем

Выражая нормальное напряжение _z из (1.3), получим

Таким образом, при растяжении-сжатии в поперечных сечениях стержня возникают нормальные напряжения, определяемые отношением продольной силы к площади сечения.

2.2 Деформации и перемещения. Закон Гука при растяжении или сжатии

При растяжении-сжатии возникают продольные и поперечные деформации. Рассмотрим их более подробно (рисунок 2.3).

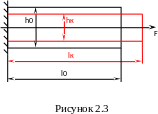
Здесь:

l₀ и h₀ – размеры стержня до деформации;

l_к и h_к – размеры стержня после деформации;

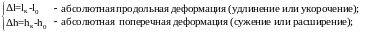
Относительные деформации  и  – величины безразмерные или могут измеряться в процентах.

Отношение поперечной деформации к продольной является константой материала, которая называется коэффициентом поперечной деформации или коэффициентом Пуассона:

Для реальных материалов коэффициент Пуассона изменяется в следующих пределах

0   0,5.

Так, этот коэффициент равен:

- для пробкового дерева  = 0;

- стали  = 0,3;

- каучука  = 0,5.

При помощи коэффициента Пуассона можно определить поперечную деформацию через продольную и наоборот:

Продольная деформация и нормальные напряжения при растяжении-сжатии связаны между собой законом линейной пропорциональности, который называется законом Гука - продольные деформации изменяются пропорционально изменению нормальных напряжений:

(2.7)

где E – модуль упругости первого рода (модуль Юнга) – это физическая постоянная материала, характеризующая его упругие свойства, численно равная нормальному напряжению, которое вызывает деформацию, равную единице:

Модуль упругости первого рода принимает значение:

- для стали Е_сталь = (1,9…2.2)10⁵ МПа;

- чугуна Е_чугун = 1,210⁵ МПа.

Закон Гука (2.7) иногда применяется и в таком виде:

 = Е .

(2.9)

Пользуясь законом Гука, получим зависимость для нахождения абсолютных деформаций при растяжении-сжатии

здесь EA характеризует жесткость сечения стержня, ;

Зависимость (2.10) выражает закон Гука для абсолютной деформации при растяжении-сжатии.

При нахождении полной деформации ступенчатого стержня определяют сумму деформаций отдельных степеней стержня (рисунок 2.4).

В некоторых случаях возникает необходимость в нахождении перемещений точек стержня по отношению к какому-либо сечению (например, к месту закрепления). В этом случае перемещение, представляющее собой изменение местоположения искомого сечения, найдется как абсолютная деформация участка бруса, заключенного между заданными сечениями (рисунок 2.4):

(2.12)

2.3 Экспериментальное изучение механических свойств материалов.

Испытание на растяжение

Экспериментальные исследования выполняются с целью изучения механических свойств материалов, проверки точности расчетных формул, оценки работоспособности проектируемой конструкции на лабораторных моделях. Лабораторные испытания материалов производят при различных деформациях, таких как растяжение, сжатие, сдвиг, кручение, изгиб.

Одним из наиболее важных видов экспериментальных исследований является одноосное испытание на растяжение, т.к. при этом определяются наиболее важные механические характеристики материалов. Для испытания применяются лабораторные образцы цилиндрической формы (рисунок 2.5) или плоской формы (рисунок 2.6), размеры и режим нагружения которых соответствуют ГОСТ 1497-84.

Для испытаний на растяжение применяют разрывные машины, позволяющие в процессе испытания определять усилия и соответствующие им деформации образца. В результате проведенного испытания получают диаграмму растяжения, в которой по оси ординат откладываются усилия, а по оси абсцисс – соответствующие им удлинения. Типичный вид такой диаграммы для малоуглеродистой стали изображен на рисунке 2.7.

После обработки экспериментальных данных определяются механические характеристики прочности и пластичности. К характеристикам прочности, МПа, относятся:

- предел пропорциональности σ_пц;

- предел упругости σ_уп;

- предел текучести σ_т;

- предел прочности σ_в ,;

- напряжение в момент разрыва - условное и истинное σ_р^у, σ_р^и .

К характеристикам пластичности, %, относятся:

- относительное удлинение при разрыве δ;

- относительное сужение при разрыве ψ.

Также определяются энергетические характеристики материала:

- полная работа Р, затраченная на разрушение образца, Дж;

- удельная работа р, затраченная на разрушение образца, Дж/м³.

Основными характеристиками прочности материалов, которые используются в практических расчетах как предельные напряжения, являются предел временного сопротивления разрыву (предел прочности) и предел текучести .

Предел текучести является напряжением, опасным обычно для пластичного материала, а предел прочности - для хрупкого.

2.4 Основные принципы расчета элементов конструкции. Условия и виды расчетов при растяжении-сжатии

В курсе прикладной механики расчет элементов конструкций производится в основном по принципу допускаемых напряжений, исходя из условий прочности и жесткости, и сводится к выполнению трех видов расчета.

Принцип допускаемых напряжений (П.Д.Н.) – принимает в качестве критерия работоспособности конструкции наибольшее напряжение, которое не должно превышать допускаемого значения материала этой конструкции, т.е.

где [] – допускаемое напряжение, превышение которого (с некоторым запасом) может привести к разрушению конструкции; оно определяется как отношение предельного напряжения к коэффициенту запаса прочности:

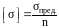
(2.14)

В качестве предельного напряжения принимается:

– для пластичного материала – предел текучести _т с целью предотвращения появления остаточных деформаций;

– для хрупкого материала – предел прочности _в для предотвращения полного разрушения материала;

- n – коэффициент запаса прочности – принимается по специальным нормативным документам, с учетом таких факторов, как ответственность конструкции, срок ее эксплуатации, точность нахождения действующих нагрузок, правильность расчетных формул и пр. Коэффициент запаса прочности изменяется, соответственно, для пластичных и хрупких материалов в следующих пределах:

n_пласт. = 1,5 - 2,0;

n_хруп. = 1,8  -2,5.

Для растянутого или сжатого стержня должны выполняться, соответственно, следующие условия прочности и жесткости:

(2.15)

(2.16)

По условиям (2.15) и (2.16) можно выполнить три основных вида расчетов: проверочный, проектировочный и нахождение максимальной грузоподъемности конструкции.

Рассмотрим эти виды расчетов на примере условия прочности (2.15):

- при проверочном расчете известна внешняя нагрузка, размеры и материал конструкции; необходимо найти _max. Проверка выполняется по условию (2.15);

- при проектировочном расчете известно N_max и []; необходимо найти A; условие проектировочного расчета имеет вид

- при расчете максимальной грузоподъемности известно A, []; необходимо найти N_max; обращаясь к условию (2.15), находим N_max:

При выполнении расчетов одновременно по условию прочности и условию жесткости в конечном итоге выбираем то значение искомого параметра, которое одновременно отвечает как условию прочности, так и условию жесткости.

3 ИСХОДНЫЕ ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ РАСЧЕТНО-ПРОЕКТИРОВОЧНОЙ РАБОТЫ

Задача 1 - Построение эпюры крутящего момента

1 Вычертить схему вала и разбить его на силовые участки.

2 Записать уравнение крутящего момента для каждого силового участка, используя метод сечений.

3 Определить величину крутящего момента в характерных сечениях.

4 По результатам расчетов построить эпюру крутящего момента.

Исходные данные приведены в таблице 1, расчетная схема - на рисунке 1.

Таблица 1- Исходные данные к задаче 1

Номер варианта	0	1	2	3	4	5	6	7	8	9
m, Н·м	5	10	15	20	25	30	35	40	45	50

Задача 2 - Расчеты на прочность при растяжении – сжатии

1 Вычертить схему бруса.

2 Построить эпюру продольной силы по методу сечений.

3 Построить эпюру нормальных напряжений.

4 Из условия прочности при растяжении-сжатии определить характерный размер сечения бруса.

5 Определить абсолютную деформацию бруса.

Исходные данные приведены в таблице 2, расчетная схема - на рисунке 2.

Таблица 2 – Исходные данные к задаче 2

Вариант	0	1	2	3	4	5	6	7	8	9
а, м	0,12	0,18	0,24	0,36	0,48	0,30	0,36	0,42	0,40	0,36
F1, кН	10	20	30	40	50	60	20	30	50	60
F2, кН	40	10	20	30	40	50	60	20	30	50
F3, кН	50	40	10	20	30	40	50	60	20	30
q, кН/м	5	0	20	30	40	50	60	70	80	90

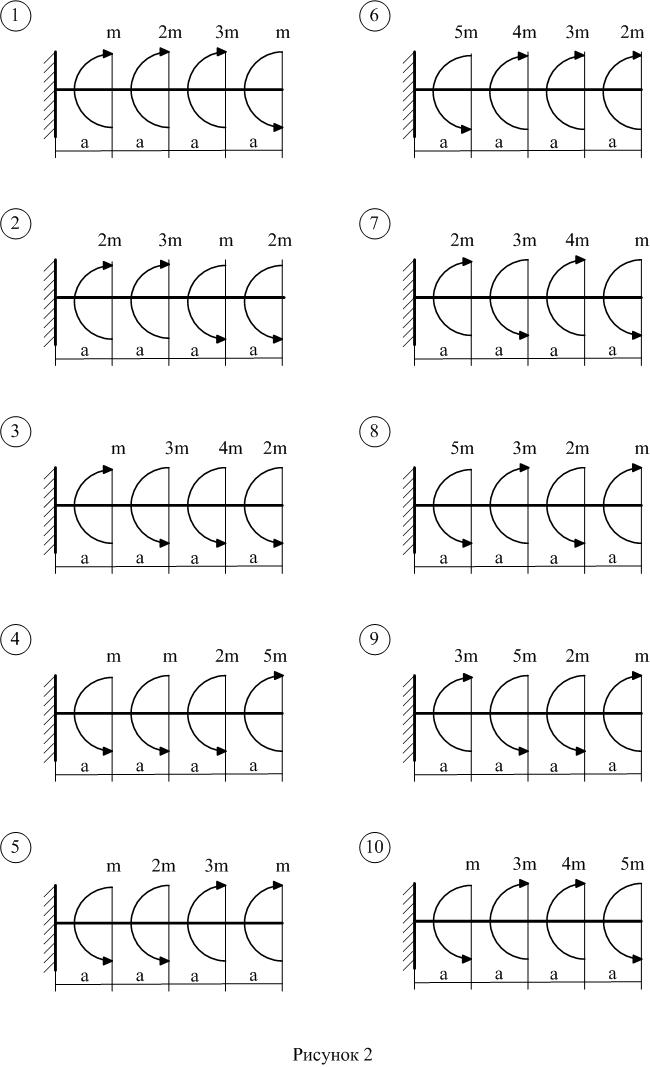
Рисунок 1

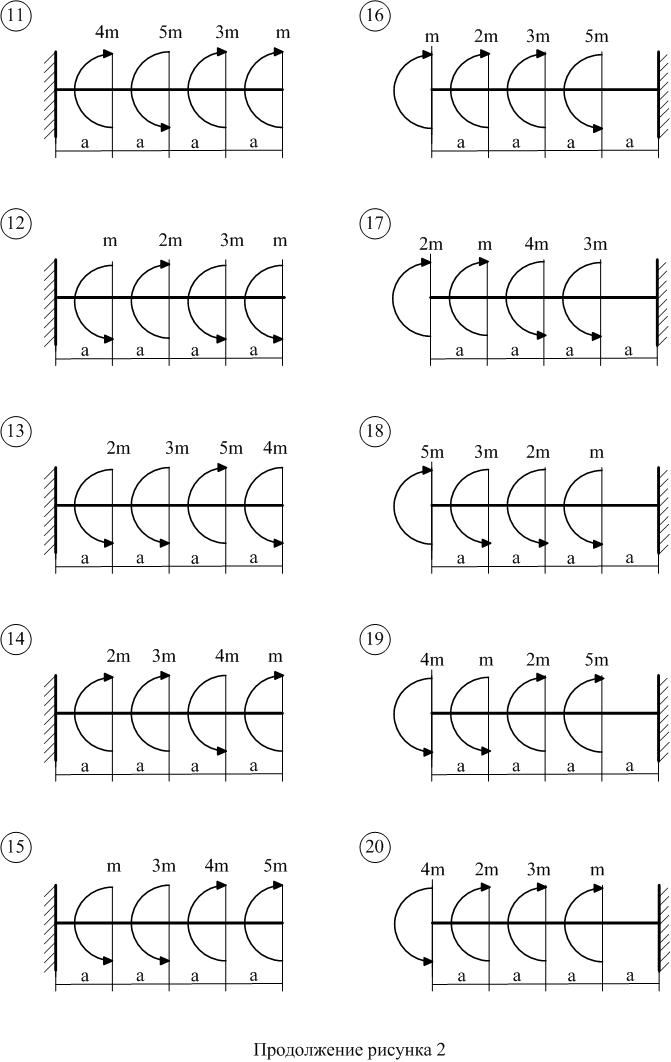
Продолжение рисунка 1

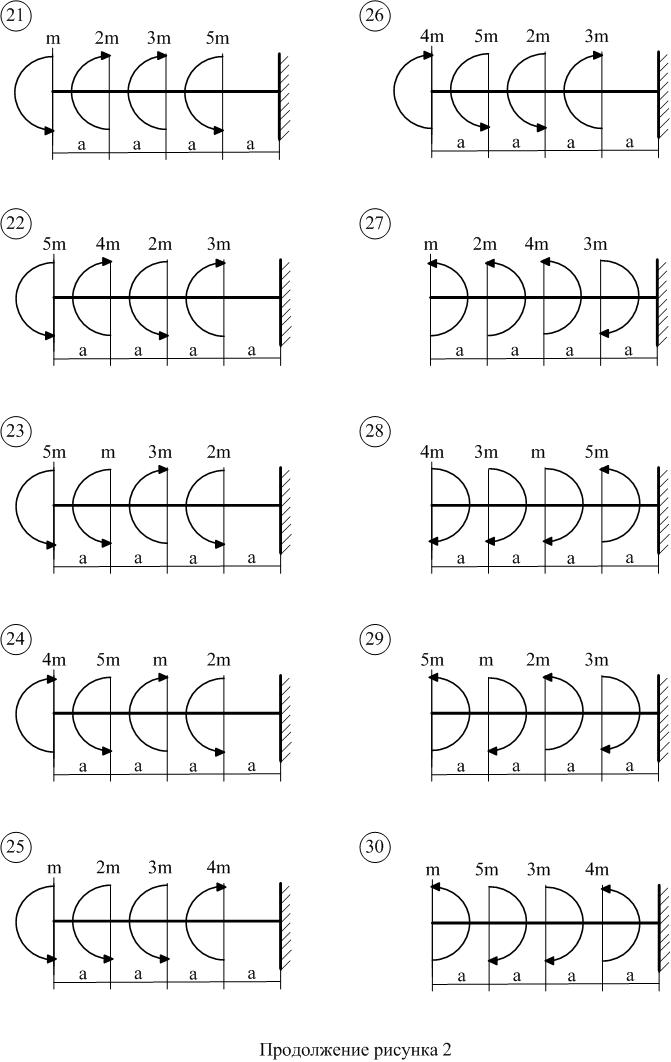
Продолжение рисунка 1

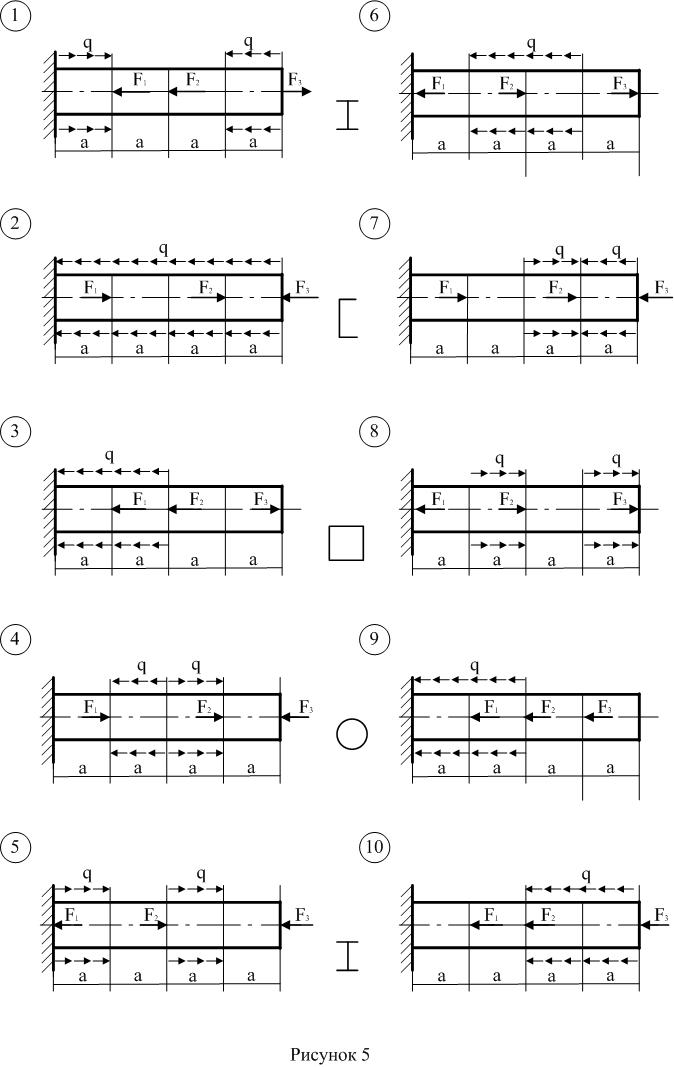
Рисунок 2

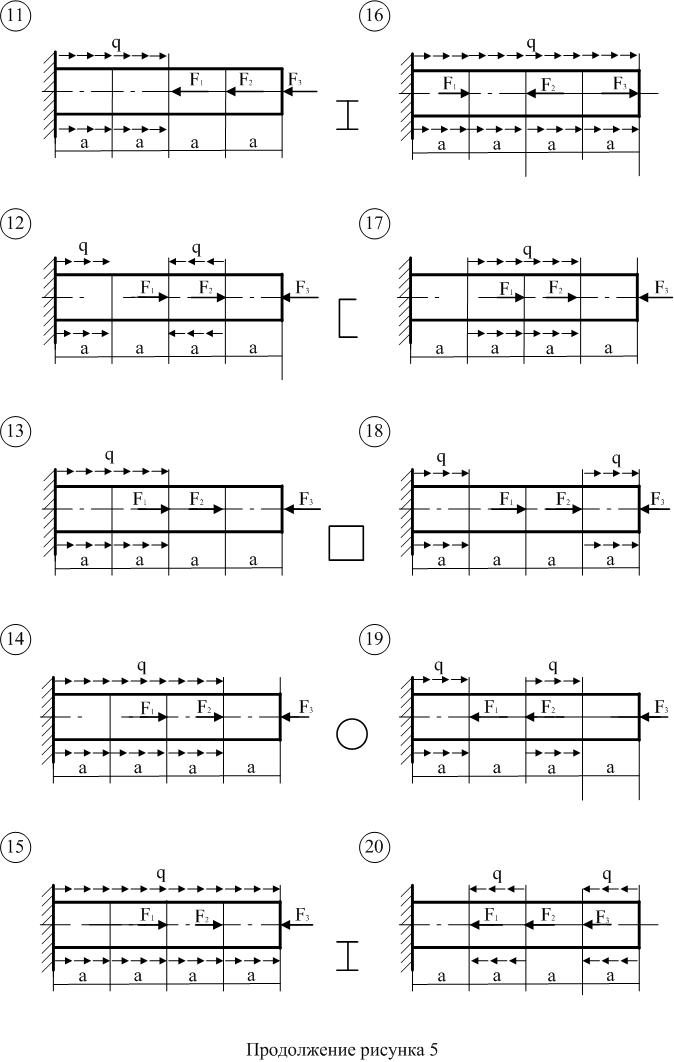
Продолжение рисунка 2

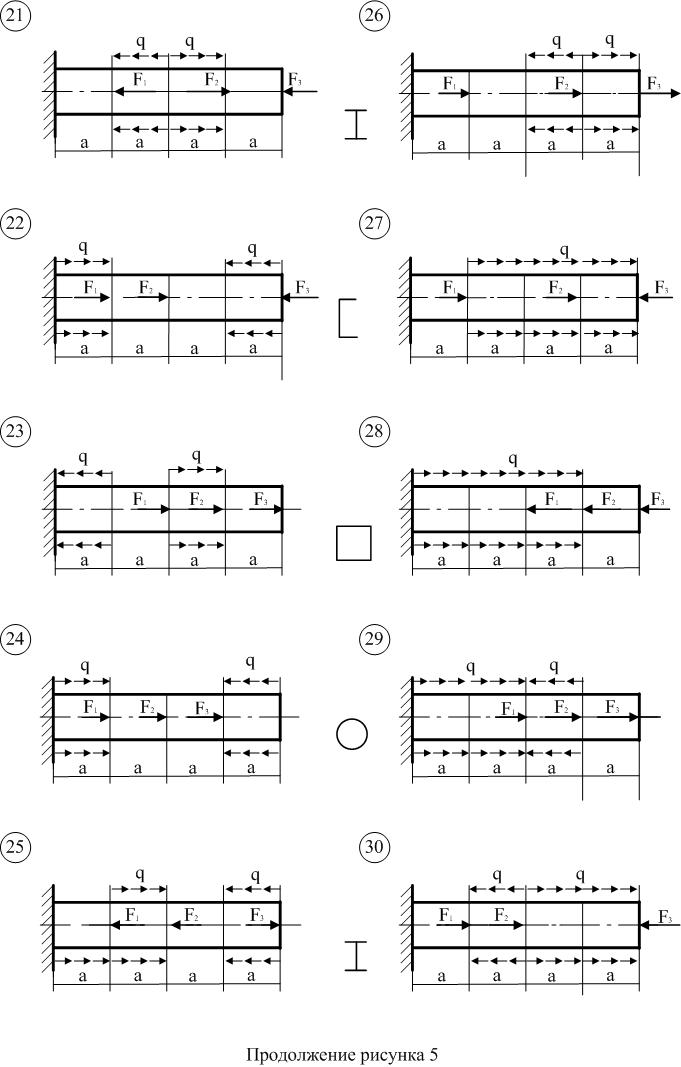
Продолжение рисунка 2

ПРИЛОЖЕНИЕ А

Примеры решения задач расчетно-проектировочной работы

Задача 1 - Построение эпюры крутящего момента

Исходные данные: 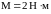, 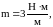а = 1 м.

Заданная схема вала представлена на рисунке 1.