26. Способ вращения вокруг проецирующих прямых
Сущность метода состоит в том, что, сохраняя основную систему ПП (П1/П2) неизменной, проецируемым отрезкам прямых, плоским фигурам придаем путем вращения вокруг некоторой оси частное положение по отношению к ПП. В случае, если отрезок повернуть до положения, паралл. ПП, то на эту ПП он проецируется в н.в. В качестве осей вращения применяют прямые, перпенд ПП, расп. вне этих плоскостей или принадлежащие им.
28. Способ вращения вокруг прямых уровня.
При опр. формы и размеров плоских фигур применяется метод вращения вокруг гориз/фронтали.
Для определения нового положения точки А на чертеже:
выбрать положение оси
из ГП (А1) провести перпенд к h1
О – центр вращения, ОА – радиус вращения
опр н.в. радиуса вращения О1А0 и отложить его на пр-нии О1А1. Получаем ГП А1, которая расположена на одном уровне с горизонталью, поэтому А2 проецируется на h2.
29. Способ совмещения
Вращение плоскости вокруг её следа примен. в случаях, когда надо, например, определить н.в. отрезка, пл. фигуры и т.д., расп. в данной плоскости. Чтобы добиться этой цели, надо вращать плоскость вокруг её следа до совмещения с П1 или П2.
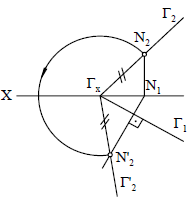
Г2 совместить с П1:
из Гx провести дугу радиусом ГxN2 до пересеч. с прямой, перпенд Г1, проходящей из точки N1.
30. Пересечение многогранника плоскостью частного положения.
Для определения линии пересечения надо воспользоваться несколькими вспомогательными построениями
Метод ребер:
- нахождение точек пересечения ребер многогр. с плоскостью, т.е. нахождение вершин многоугольника, получ. в сечении
Метод граней:
-нахожд. линий пересеч. граней с секущей плокостью, т.е. нахожд. сторон сечения
31. Пересечение многогранников прямой линией
Прямая может пересекать многогранник в 2 точках при условии, что он выпуклый.
1 - через прямую провести вспом. плоскость
2 - проекция фигуры сечения
- опр. точки пересечения прямой с контуром сечения
32. Пересечение многогранника плоскостью общего положения.
В этом случае получается плоский многоугольник. Его можно построить по точкам пересечения с плоскостью рёбер или по линиям пересечения граней с плоскостью. Задача сводится к определению точки пересечения прямой с плоскостью или к определнию линии пересечения плоскостей.
Первый способ применяется чаще второго
Плоская фигура, полученная от пересечения многогранника плоскостью - сечение.
35. Пересечение поверхности вращения прямой линией
Для построения точки пересечения прямой с какой-либо поверхностью надо провести через прямую вспомог. сек. плоскость; затем найти линию пересечения вспом. плоскости с данной поверхностью и определить точку пересечения линии с данной прямой. Эти точки и будут искомыми точками пересечения прямой с поверхностью.
Вспомог. плоскость следует выбирать так, чтобы получались простейшие сечения. В ряде случаев показ. вспом плоскости излишен.