7. Определение

Базовыми элементами, которыми оперирует алгебра логики, являются высказывания. Высказывания строятся над множеством {B,  ,  ,  , 0, 1}, где B — непустое множество, над элементами которого определены три операции:

 отрицание (унарная операция),

 конъюнкция (бинарная),

 дизъюнкция (бинарная),

а также константы — логический ноль 0 и логическая единица 1.

Дизъю́нкт — пропозициональная формула, являющаяся дизъюнкцией одного или более литералов (например  ). Конъюнкт — пропозициональная формула, являющаяся конъюнкцией одного или более литералов (например  ).

[Править]Аксиомы

1. , инволютивность отрицания, закон снятия двойного отрицания

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

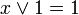
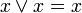
[Править]Логические операции

Простейшим и наиболее широко применяемым примером такой алгебраической системы является множество B, состоящее всего из двух элементов:

B = { Ложь, Истина }

Как правило, в математических выражениях Ложь отождествляется с логическим нулём, а Истина — с логической единицей, а операции отрицания (НЕ), конъюнкции (И) и дизъюнкции (ИЛИ) определяются в привычном нам понимании. Легко показать, что на данном множестве B можно задать четыре унарные и шестнадцать бинарных отношений и все они могут быть получены через суперпозицию трёх выбранных операций.

Опираясь на этот математический инструментарий, логика высказываний изучает высказывания и предикаты. Также вводятся дополнительные операции, такие как эквивалентность  («тогда и только тогда, когда»), импликация   («следовательно»), сложение по модулю два   («исключающее или»), штрих Шеффера  , стрелка Пирса   и другие.

Логика высказываний послужила основным математическим инструментом при создании компьютеров. Она легко преобразуется в битовую логику: истинность высказывания обозначается одним битом (0 — ЛОЖЬ, 1 — ИСТИНА); тогда операция   приобретает смысл вычитания из единицы;   — немодульного сложения; & — умножения;   — равенства;   — в буквальном смысле сложения по модулю 2 (исключающее Или — XOR);   — непревосходства суммы над 1 (то есть A   B = (A + B) <= 1).

Впоследствии булева алгебра была обобщена от логики высказываний путём введения характерных для логики высказываний аксиом. Это позволило рассматривать, например, логикукубитов, тройственную логику (когда есть три варианта истинности высказывания: «истина», «ложь» и «не определено») и др.

[Править]Свойства логических операций

1. Коммутативность: x y = y x,  {&,  }.

2. Идемпотентность: x x = x,  {&,  }.

3. Ассоциативность: (x y) z = x (y z),  {&,  }.

4. Дистрибутивность конъюнкций и дизъюнкции относительно дизъюнкции, конъюнкции и суммы по модулю два соответственно:

   • ,

   • ,

   • .

5. Законы де Мо́ргана:

   • ,

   • .

6. Законы поглощения:

   • ,

   • .

8. Таблицы истинности для основных двоичных логических функций

Конъюнкция	Дизъюнкция	Сложение по модулю 2
Импликация		Эквиваленция
Штрих Шеффера	Стрелка Пирса	Отрицание

9. Теоремы для одной переменной:

A \/ 0 = A           4. A \/ Ā = 1         7. A · A = A

2. A \/ 1 = 1           5. A · 0 = 0         8. A · Ā = 0

3. A \/ A = A           6. A · 1 = 1         9. 

10) Теоремы для двух и более переменных:

10. а) A \/ B = B \/ A,         б) AB = BA

переместительный закон, означает, что все входы логического элемента равнозначны.

11. а) A \/ B \/ C = A \/ (B \/ C) = (A \/ B) \/ C,

б) ABC = A(BC) = (AB)C – сочетательный закон.

12. а) A (B \/ C) = AB \/ AC, б) A \/ BC = (A \/ B)(A \/ C) – распределительный закон.

Данная теорема и все последующие вытекают из принципа двойственности. Применим его к выражению 12, а:

– левая часть,

– правая часть.

Введя новые обозначения:  , получим обозначения:  , а это и есть теорема 12, б.

13. а) A \/ AB = A, б) A(A \/ B) = A

– закон поглощения (A поглощает B).

Доказательство 13, а:

A \/ AB = A(1 \/ B) = A · 1 = A, (используя теоремы 2, 6).

Теорема 13, б следует из принципа двойственности.

14. а)  , б)  .

Доказательство 14.а:

, (используя теоремы 8 и 1).

Теорема 14, б следует из принципа двойственности.

15. а) AB \/ ĀB = B, į) (A \/ B)(Ā \/ B) = B, закон склеивания (склеивание по A).

Доказательство 15, а:

AB \/ ĀB = B(A \/ Ā) = B · 1 = B, (используя теоремы 4 и 6).

Теорема 15, б следует из принципа двойственности.

13,14,15) COPY — копировать в другое место один или несколько файлов DEL / ERASE — удалить один или несколько файлов FC — сравнить два файла (набора файлов) и вывести различия между ними FIND — найти в одном или нескольких файлах текстовую строку MD / MKDIR — создать папку MOVE — переместить из одной папки в другую один или несколько файлов PRINT — вывести содержимое текстового файла на печать RD / RMDIR — удалить папку REN / RENAME — переименовать файл или папку REPLACE — заместить файлы ROBOCOPY — запустить улучшенное средство копирования файлов и деревьев каталогов TREE — вывести графическую структуру каталогов диска или папки TYPE — вывести содержимое текстовых файлов на экран XCOPY — копировать файлы и деревья каталогов

Кроме работы с файлами и папками, команды командной строки позволяют работать с жесткими дисками компьютера и их файловыми системами: изменять метку диска, выполнять проверку диска на наличие ошибок, изменять файловую систему диска. Эта группа команд включает такие команды:

CHKDISK — проверить диск и вывести статистику CHKNTFS — отобразить или изменить выполнение проверки диска при загрузке COMPACT — отобразить и изменить сжатие файлов в разделах NTFS CONVERT — преобразовать дисковый том FAT в NTFS (для текущего активного диска преобразование выполнить нельзя) DISKPART — отобразить и настроить свойства раздела диска FORMAT — форматировать диск (осторожно: форматирование удаляет все данные на диске!) FSUTIL — отобразить и настроить свойства файловой системы LABEL — создать, изменить или удалить метку тома для диска RECOVER — восстановить данные с плохого или поврежденного диска (если их можно прочитать) VOL — вывести метку и серийный номер тома для диска

Есть команды командной строки, позволяющие узнать определенную информацию о системе (версия, конфигурация, установленные драйвера):

DRIVERQUERY — отобразить текущее состояние и свойства драйвера устройства SYSTEMINFO — вывести информацию о системе и конфигурации компьютера VER — вывести на экран сведения о версии Windows

Но параметры системы можно не только просматривать, но и изменять — к примеру, устанавливать системную дату и время. Кроме этого, команды командной строки позволяют управлять приложениями и процессами и даже выключать компьютер.

DATE — вывести или установить текущую дату SCHTASKS — выполнить команду или запустить приложение по расписанию SHUTDOWN — выключить компьютер (локально или удаленно) TASKLIST — отображение всех выполняемых задач (в т.ч. служб) — аналог диспетчера задач TASKKILL — прекратить или остановить процесс или приложение (для остановки используется идентификатор процесса — PID, который можно узнать при помощи команды TASKLIST)  TIME — вывести и установить системное время

Есть группа команд, которые позволяют управлять самой командной строкой: изменять ее внешний вид, запускать еще одну копию, очищать экран.

CLS — очистить экран командной строки  CMD — запустить еще одну копию командной строки COLOR — установить цвет текста и фона командной строки PROMPT — изменить приглашение в командной строке TITLE — назначить заголовок окна для текущего сеанса cmd.exe (интерпретатора командной строки) EXIT — выйти из командной строки

17) Представление текстовой информации

(пример)

© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ» 3

mom soap frame

+

.0 .1 .2 .3 .4 .5 .6 .7 .8 .9 .A .B .C .D .E .F

6. ` a b c d e f g h i j k l m n o

7. p q r s t u v w x y z { | } ~ DL

=

m o m s o a p f r a m e

6D 6F 6D 20 73 6F 61 70 20 66 72 61 6D 65

Хранение текстовой информации

(строки)

Описанный способ представления предполагает

описание текста в виде набора однотипных данных.

Для хранения подобной информации в языках

высокого уровня (например, СИ) применяются

массивы – строки.

Для хранения одного символа в языке СИ

предусмотрен тип данных char.

Хранение текста, приведенного на предыдущем

слайде, может быть организовано в массиве:

char text[14];

19) Компилятор - Программа, выполняющая компиляцию. Компилятор создает выполняемый файл из программы, написанной на языке программирования высокого уровня. Недостатком компилятора является невозможность во время программирования проверить работу отдельной команды. Однако, увеличение скорости компиляции, появление структурного программирования и мощных отладчиков делают это практически незаметным. В настоящее время компиляторы распространены больше, чем интерпретаторы. Примерами компиляторов являются программы Turbo Pascal, Turbo C, Quick C. Большинство систем управления базами данных (например, Fox) совмещают в себе и интерпретатор, и компилятор.  Интерпретатор - Устройство, которое имеет сообщение на входе и преобразует его в другое на выходе. В этом смысле каждый компьютер - интерпретатор. 2. Тип реализации транслятора языка программирования высокого уровня, при котором не существует отдельно текста программы на машинном языке (как у компилятора), а существует исходный текст, и машина пытается выполнять каждую языковую команду, представляя (интерпретируя) ее в командах нижнего уровня. В этом смысле операционная система - это интерпретатор, который работает с файлами. Выстраивается следующая схема: - на нижнем уровне процессор интерпретирует входные сигналы в выходные; - на следующем уровне находится программное средство, называемое операционной системой, которое текст (например, имя запускаемой программы) интерпретирует в результат; - на третьем уровне может находиться еще один язык-интерпретатор (например, Бейсик) и в нем может интерпретироваться программа пользователя. Существуют компьютеры, у которых операционная система совмещена с языком Бейсик, что уменьшает тем самым количество интерпретаций. Достоинства языка интерпретирующего типа: программа существует только на языке интерпретатора, что упрощает работу. Недостаток: медленная скорость выполнения программы, в связи с тем, что каждый раз при ее запуске программы необходимо проводить трансляцию, т.е. трансляция проходит непосредственно перед моментом выполнения каждой команды. Самыми характерными примерами интерпретаторов являются многие реализации языка Бейсик (MSX-Basic, GW-Basic), хотя существуют и реализации, поддерживающие компиляцию (QuickBasic, TurboBasic).

20)

21)

Константа	Формат	Примеры
Логическая	Обозначается ключевым словом true или false	true, false
Целая	Десятичный: последовательность десятичных цифр, начинающаяся не с нуля, если это не число нуль	8, 0, 199226
	Восьмеричный: нуль, за которым следуют восьмеричные цифры (0, 1, 2, 3, 4, 5, 6, 7)	01, 020, 07155
	Шестнадцатеричный: 0х или 0Х, за которым следуют шестнадцатеричные цифры (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F)	0xA, 0x1B8, 0X00FF, 0X00ff
Вещественная	Десятичный: [цифры].[цифры]	5.7, 0.001, 35
	Экспоненциальный: [цифры][.][цифры]{E|e}[+|-][цифры]	0.2E6, .11e-3, 5E10, 1.22E-10
Символьная	Один или более символов, заключенных в апострофы	'A', 'ю', '*', 'db', 'A', '\n', '\012', '\x07\x07'
Строковая	Последовательность символов, заключенная в кавычки	"Здесь был Vasia", "\tСумма =\xF5\n"