25. Дисконтирование и его использование в экономическом анализе

Дисконтированием называется исчисление первоначальной суммы денег на основании ее конечной величины.

Дисконтирование – обратная операция по отношению к нахождению будущей стоимости.

В общем случае вопрос звучит так: какую сумму денег (K₀) надо положить сегодня на счет, чтобы через год там было K₁ р., если процентная ставка составляет i% годовых?

Ответ:

Поставим вопрос в самом общем виде: какую сумму денег надо положить сегодня в банк, чтобы через n лет на счете было K_n р.? Ответ будет зависеть от того, какой процент начисляет банк: простой или сложный.

Если процент простой, то:

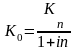
Если процент сложный, то:

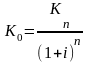
Путем дисконтирования можно определить, какой сумме денег сегодня эквивалентна некоторая сумма, которая будет получена в будущем (FV).

Таким образом, можно рассчитать приведенную стоимость будущих денежных поступлений (PV).

Важнейший постулат финансового анализа состоит в том, что деньги имеют различную временную ценность. Это объясняется возможным альтернативным использованием денежных средств.

В общем виде, обозначив сумму, получаемую через год – FV₁можно получить ее приведенную стоимость:

Таким образом, при начислении сложных процентов приведенная стоимость денег, которые будут получены через n лет (FV_n), рассчитывается по формуле:

Если ежегодно получаемая сумма денег составляет (FV_j) р. в течение n лет, то приведенная стоимость всей суммы будущих поступлений составит:

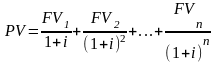
Если доход, получаемый каждый год постоянен (FV), имеем геометрическую прогрессию со знаменателем 1/(1+i):

Отсюда:

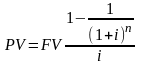
Если число лет бесконечно велико (n), формула упрощается:

На основе дисконтирования можно решать задачи на погашение займов. Пусть некто взял заем под сложные i% годовых. Выплата в j-ый год составляет FV_j. Продисконтировав эту выплату по процентной ставке, находим ее приведенную стоимость:

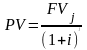
В момент, когда сумма всех дисконтированных выплат становится равна первоначальному долгу, последний считается погашенным.