28.Первый зам предел о синусе.
Пусть, начиная с некоторого , выполняются неравенства , причем крайние переменные имеют одинаковый конечный предел , тогда переменная также имеет предел, причем тот же самый.
Доказательство:
Возьмём любое , по определению предела начиная с некоторого номера будут выполняться неравенства:
и
В силу неравенств (*) выполняется неравенство (начиная с некоторого номера ):
Это и означает, что переменная имеет пределом .
, ч. т. д.
(об ограниченности переменной, имеющей конечный предел).
Пусть переменная имеет конечный предел , тогда эта переменная является ограниченной переменной, что означает, что при всех n имеет место неравенство , где и – некоторые постоянные числа.
Доказательство:
Возьмем производную , по определению предела существует такой номер ,что при следует выполнение неравенства:
Значение переменной, которые могут не удовлетворять неравенство (*) лишь конечное число:
Рассмотрим множество чисел: выберем из них самое большое и обозначим , тогда при всех выполняется: , ч. т. д.
28.Первый замечательный предел (о синусе).
Если
угол х выражен в радианах, то 
.
Первый замечательный предел можно
применять в ряде случаев для раскрытия
неопределенностей вида 
.
Пример.
Найти предел функции 
.
Решение. Здесь неопределенность вида
.
Преобразуем данную функцию: 
.
Обозначим 12х=U, причем
т.е.
при х => 0 и U => 0. Следовательно, 
.
Аналогично, положив 3x=U , получим 
.
Следовательно 
Ответ: 4.
Пример.
Найти 
.
Имеем неопределенность вида 
.
Решение. Обозначим arctg 6x = U, тогда
6х= tgU и при х => 0 имеем U =>
0. Следовательно,
29.Второй
зам предел об экспоненте.
Он
имеет вид: 
,
где е –
иррациональное число, приблизительно
равное 2,71828… .
Логарифмы
с основанием е называются
натуральными и обозначаются
logex =ln 1.0pt'>x.
С помощью этого предела раскрывают так
же неопределенность вида {1∞}.
Пример .
Найти 
.
Здесь неопределенность вида {1∞}.
Решение. Преобразуем выражение в
скобках.
.
Обозначим 
,
тогда 
, 
, 
,
причем при n => ∞, имеем α => 0.
Следовательно,
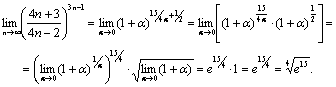Ответ: 
.
30. Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.
Бесконечно малая величина
Последовательность 
называется бесконечно
малой,
если 
.
Например, последовательность чисел 
—
бесконечно малая.
Функция
называется бесконечно
малой в окрестности точки 
,
если 
.
Функция
называется бесконечно
малой на бесконечности,
если 
либо 
.
Также
бесконечно малой является функция,
представляющая собой разность функции
и её предела, то есть если 
,
то 
, 
.
Определения
Допустим,
у нас есть бесконечно малые при одном
и том же 
величины 
и 
(либо,
что не важно для определения, бесконечно
малые последовательности).
Если
,
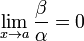то 
—
бесконечно малая высшего
порядка малости,
чем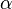 
.
Обозначают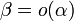 
.Если
,
то
—
бесконечно малая низшего
порядка малости,
чем
.
Соответственно 
.Если
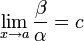(предел
конечен и не равен 0), то
и
являются
бесконечно малыми величинами одного
порядка малости.
Это
обозначается как 
или 
(в
силу симметричности данного отношения).
Если
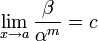(предел
конечен и не равен 0), то бесконечно
малая величина
имеет 
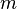-й
порядок малости относительно
бесконечно малой
.
Для вычисления подобных пределов удобно использовать правило Лопиталя.