
- •1 Матрицы и действия над ними.
- •4. Обратная матрица.
- •5. Метод Крамера
- •6.Решение систем линейных уравнений матричным методом.
- •7.Элементарные преобразования и ранг матрицы.
- •9.Векторы и действия над ними.
- •3)Умножение вектора на число
- •10. Декартовы координаты вектора в пространстве.
- •11.Скалярное произведение вектора.
- •12.Скалярное произведение в координатах.
- •13. Условие ортогональности двух векторов:
- •14.Векторное произведение.
- •15.Векторное произведение через координаты векторов.
- •16.Условие коллинеарности векторов.
- •18.Выражение смешанного произведения векторов.
- •19.Плоскость в трехмерном пространстве и ее уравнение.
- •20.Взаимное расположение двух плоскостей.
- •22.Взаимное расположение двух прямых.
- •25. Взаимное расположение двух прямых на плоскости
- •26.Пределы последовательностей и функции.
- •27.Основные теоремы о пределах. О сжатой переменной. О ограниченнойфункции.
- •28.Первый зам предел о синусе.
- •Определения
- •Примеры сравнения При величина имеет высший порядок малости относительно , так как . С другой стороны, имеет низший порядок малости относительно , так как .
- •Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака. Бесконечно большая величина
- •31.Теорема о конечных пределах.(сумма произведения частного)
- •32.Непрерывность и разрывы функции. Классификация разрывов.
- •33.Производная функция и ее геометрический смысл.
- •34.Правило деффиринциирования и таблица производных Правила дифференцирования
- •35.Деффиринциал и его геометрический смысл.
- •36.Производные деффиринциалы высших порядков.
- •37.Теоремы Роля и Лагранжа.(?)
- •38.Теорема Коши.Теорема и правило Лопиталя(???))
- •Точная формулировка
- •39.Формула Тэйлора. Формула Тейлора
- •40.Исследование возр убыв экстремумов выпуклости вогнутости ф-ий.(?)
- •2.5.3. Экстремумы функции
25. Взаимное расположение двух прямых на плоскости
|
Если две прямые l1 и l2 лежат на плоскости, то возможны три различных случая их взаимного расположения: 1)пересекаются (т.е. имеют одну общую точку); 2) параллельны и не совпадают; 3) совпадают. Выясним, как узнать, какой из этих случаев имеет место, если эти прямые заданы своими уравнениями в общем виде:
Если прямые l1 и l2 пересекаются в некоторой точке М(х,у), то координаты этой точки должны удовлетворять обоим уравнениям системы (12). Следовательно, чтобы найти координаты точки пересечения прямых l1 и l2, надо решить систему уравнений (12): 1) если система (12) имеет единственное решение, то прямые l1 и l2 пересекаются; 2) если система (12) не имеет решения, то прямые l1 и l2 параллельны; 3) если система (12) имеет множество решений, то прямые l1 и l2 совпадают. Условием совпадения двух прямых является пропорциональность соответствующих коэффициентов их уравнений. Пример 10. Пересекаются ли прямые 3х+4у-1=0 и 2х+3у-1=0 ? Решение: Решим систему
уравнений: Пример 11. Параллельны, ли прямые 2х-у+2=0 и 4х-2у-1=0? Решение: Решим систему
уравнений Пример 12. Совпадают ли прямые х+у+1=0 и 3х+3у+3=0? Решение: Совпадают, так как коэффициенты пропорциональны. Пример 13. Составить уравнение прямой линии, проходящей через точку пересечения прямых х+у-1=0, х-у+2=0 и через точку (2,1). Решение: Находим координаты точки
пересечения двух данных прямых линий.
Для этого решаем данные уравнения
совместно. Складывая, находим: 2х+1=0,
откуда |
26.Пределы последовательностей и функции.
27.Основные теоремы о пределах. О сжатой переменной. О ограниченнойфункции.
ТЕОРЕМА №5: (об ограниченности переменной, имеющей конечный предел).
Пусть
переменная ![]() имеет
конечный предел
имеет
конечный предел ![]() ,
тогда эта переменная является ограниченной
переменной, что означает, что при всех
n имеет место неравенство
,
тогда эта переменная является ограниченной
переменной, что означает, что при всех
n имеет место неравенство ![]() ,
где
,
где ![]() и
и ![]() –
некоторые постоянные числа.
–
некоторые постоянные числа.
Доказательство:
Возьмем
производную ![]() ,
по определению предела существует такой
номер
,
по определению предела существует такой
номер ![]() ,что
при
,что
при ![]() следует
выполнение неравенства:
следует
выполнение неравенства: ![]()
Значение
переменной, которые могут не удовлетворять
неравенство (*) лишь конечное
число: ![]()
Рассмотрим
множество чисел: ![]() выберем
из них самое большое и обозначим
выберем
из них самое большое и обозначим ![]() ,
тогда при всех
,
тогда при всех ![]() выполняется:
выполняется: ![]()
![]() ,
ч. т. д.
,
ч. т. д.
ТЕОРЕМА №6: (о сжатой переменной).
Пусть,
начиная с некоторого
,
выполняются неравенства ![]() ,
причем крайние переменные имеют
одинаковый конечный предел
,
тогда переменная
,
причем крайние переменные имеют
одинаковый конечный предел
,
тогда переменная ![]() также
имеет предел, причем тот же самый.
также
имеет предел, причем тот же самый.
Доказательство:
Возьмём любое , по определению предела начиная с некоторого номера будут выполняться неравенства:
![]() и
и ![]()
В силу неравенств (*) выполняется неравенство (начиная с некоторого номера ):
![]()
Это и означает, что переменная имеет пределом .
![]() ,
ч. т. д.
,
ч. т. д.

 система
имеет единственное решение, следовательно
прямые пересекаются. Точка пересечения
прямых имеет координаты (-1;1).
система
имеет единственное решение, следовательно
прямые пересекаются. Точка пересечения
прямых имеет координаты (-1;1). Эта
система не имеет решений, следовательно
прямые параллельны.
Эта
система не имеет решений, следовательно
прямые параллельны.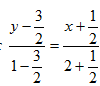 ,
или
,
или  или
или