12.Скалярное произведение в координатах.

Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов   и  . Если  то

13. Условие ортогональности двух векторов:

 или  .Т.о., для того чтобы два вектора были перпендикулярны необходимо и достаточно, чтобы сумма произведений соответствующих координат этих векторов была равна нулю.

Примеры.Пусть А(-1; 1; 0), B(3; 1; -2),  . Найти: . .

. .

.

14.Векторное произведение.

15.Векторное произведение через координаты векторов.

Выражение векторного произведения   через проекции векторов   и   на координатные оси прямоугольной системы координат дается формулой

     

которую можно записать с помощью определителя

     

Проекции векторного произведения на оси прямоугольной системы координат вычисляются по формулам

     

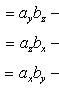
и тогда на основании (4)

     

Механический смысл векторного произведения состоит в следующем: если вектор   - сила, а вектор   есть радиус-вектор точки приложения силы, имеющий свое начало в точке O, то момент силы   относительно точки O   есть вектор, равный векторному произведению радиуса-вектора   точки приложения силы на силу  , т. е.

16.Условие коллинеарности векторов.

Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому вектору.

Так как операция умножения вектора на число соответствует сжатию или растяжению вектора при неизменном или противоположном направлении, то вектор  , где   - произвольное действительное число, коллинеарен вектору  . Справедливо и обратное утверждение: если вектор   коллинеарен ненулевому вектору  , то он может быть представлен в виде  .

Таким образом, мы пришли к необходимому и достаточному условию коллинеарности двух ненулевых векторов: для коллинеарности двух векторов   и   необходимо и достаточно, чтобы они были связаны равенствами   или  .

Перейдем к координатной форме полученного условия коллинеарности двух векторов.

Пусть вектор   задан в прямоугольной декартовой системе координат на плоскости и имеет координаты  , тогда вектор   имеет координаты   (при необходимости смотрите статью операции над векторами в координатах). Аналогично, если вектор   задан в прямоугольной системе координат трехмерного пространства как  , то вектор   имеет координаты  .

Следовательно, для коллинеарности двух ненулевых векторов   и   на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями:   или  .

Для коллинеарности двух ненулевых векторов   и   в пространстве необходимо и достаточно, чтобы   или  .

Получим еще одно условие коллинеарности двух векторов, основанное на понятии векторного произведения векторов   и  .

Если ненулевые векторы   и   коллинеарны, то по определению векторного произведения  , что равносильно равенству  . А последнее равенство возможно лишь тогда, когда векторы   и   связаны соотношениями   или  , где   - произвольное действительное число (это следует из теоремы о ранге матрицы), что указывает на коллинеарность векторов   и  . Таким образом, два ненулевых вектора   и   коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.

17.Смешанное произведение векторов и его свойство

Смешанное произведение   векторов   — скалярное произведение вектора   на векторное произведение векторов   и  :

Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).

Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами  .