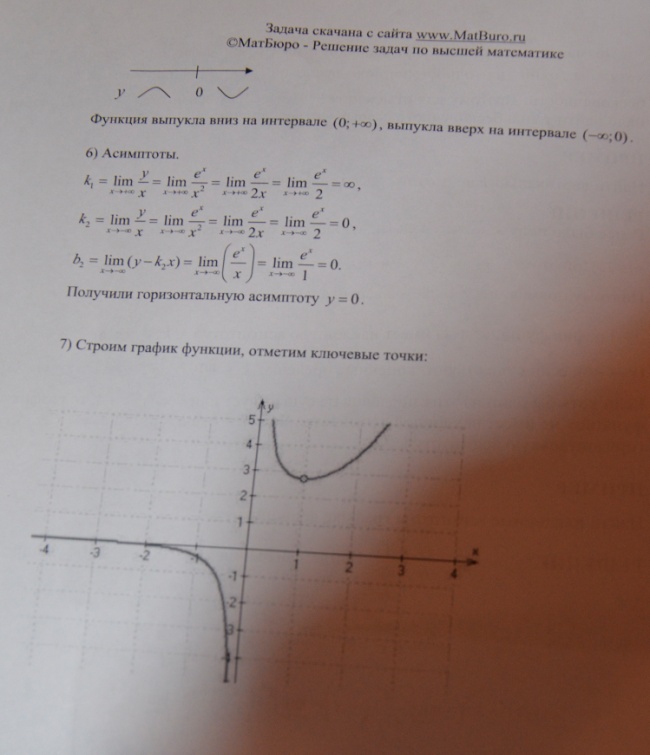
2.5.3. Экстремумы функции

Значение функции    называется максимумом функции  , если для любой точки  x  из некоторой достаточно малой окрестности точки  x_o  выполняется неравенство  . Точка  x_o  называется в этом случае точкой максимума функции  .

Значение функции    называется минимумом функции  , если для любой точки  x  из некоторой достаточно малой окрестности точки  x_o  выполняется неравенство  . Точка  x_o  называется в этом случае точкой минимума функции  .

Максимум или минимум функции называются экстремумами функции. Точка максимума или минимума функции называется точкой экстремума функции.

Необходимое условие существования экстремума: если дифференцируемая функция    достигает экстремума в точке  x_o, то ее производная первого порядка в этой точке равна нулю, т.е.  .

Точки, в которых производная    или не существует, называются критическими точками.

Достаточное условие существования экстремума: если  x_o  - критическая точка функции и при переходе через нее производная    меняет знак с плюса на минус, то точка  x_o  есть точка максимума, а значение функции    - максимум функции; если при переходе через точку  x_o  производная    меняет знак с минуса на плюс, то точка  x_o  есть точка минимума, а значение    - минимум функции; если при переходе через точку  x_o  производная знака не меняет, то экстремума в точке нет, а значение    не является экстремумом функции.

График функции    называется выпуклым в интервале  , если он расположен ниже касательной, проведенной в любой точке этого интервала.

График функции    называется вогнутым в интервале  , если он расположен выше касательной, проведенной в любой точке этого интервала.

Точка графика функции    , отделяющая выпуклую часть от вогнутой, называется точкой перегиба.

Если    в интервале  , то график функции на этом интервале вогнутый.

Если    в интервале  , то график функции на этом интервале выпуклый.

41.

42.