15. Формула Тейлора для функції кількох змінних.

Нехай функція 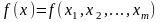, xєX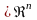 неперервна і має неперервні частинні похідні в околі т. до m-го порядку включно, то має місце формула Тейлора:

де

- многочлен Тейлора ,

- залишковий член у формі Пеано, де 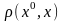, а символ означає нескінченно малу пр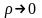и (або при 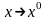) функцію більш високого порядку меншості, ніж .

Залишковий член,мзаписаний вище у формі Пеано можна також представити у формі Лагранжа, який буде мати вигляд:

.

16 Поняття локального екстремуму фкз. Необхідні умови.

Розглянемо ,

Точка 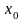назив. т-кою локального максимума (мін.) ф-ції , якщо

.

- строгий локальний макс. (мін.), якщо .

Теорема (необхідна умова екстремума)

Якщо функція визначена в околі т-ки екстремума , та якщо в цій точці існує частинна похідна , то ця похідна = 0.

В силу того, що частинна похідна по – похідна ф-ї 1 змінної, то для неї має місце т. Ферма:

Озн. Т-ка наз критичною т-кою , якщо всі частинні похідні в цій т-ці =0.

Розглянемо квадр. ф-му вигляду

є додатно (від’ємно) визначена, якщо для 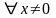A(x)>(<)0

A(x) назив. знакозмінною кв. ф. , якщо A(x’)>0, A(x”)<0.

Заув. Очевидно, для 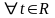виконується

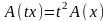
Якщо кв.ф. розглянути на проміжку , , , то знак кв.ф. зберігається на прямій .

Лема1. Якщо кв. ф. знаковизначена, то нижня межа її абсолютної величини додатня на одиничній сфері.

,

- одинична сфера, є обмеженою і замкненою множиною (компактом)

|A(x)| - неперервна ф-ція на . а тому непер. і на компакті .

|A(x)| досягає свого inf при

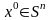
Лема 2. Якщо – кв. ф. , то прямої виконується:

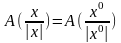.Дов. .

17. Достатні умови екстремуму функції кількох змінних.

Розглянемо квадратичну формулу: .

• А(х) наз додатньо визначеною (від’ємно) , якщо х≠0 викон: А(х)>0 (<0)

• А(х) наз знакозмінною вкадр. Формою, якщо існує х^/, х^// є такі, що викон: А(х^/)>0, А(х^//)<0.

Зауваження: t є R, A(tx) = t²A(x), A(tx) = = t²A(x)

Якщо квадратична форма розглядається на прямій, вигляду х=tx⁽⁰⁾, x⁽⁰⁾ ≠0, t є R

A(tx⁽⁰⁾)= t²A(х⁽⁰⁾). Знак квадр форми зберіг на прямій, вигляду х= tx⁽⁰⁾/{t=0}.

Лема 1. Якщо кВ форма А(х) знаковизначена, то нижня межа її абсолютної величини – додатня на одиничній сфері.

inf|A(x)|>0, де Sⁿ = {x є Rⁿ : x₁² + ….+x_n² = 1} – одинична сфера, x є Sⁿ.

Sⁿ – замкнена, обмежена множина = компакт.

|A(x)| - непер ф-я на Rⁿ → непер на компакті.

За т. Веєрштрасса: якщо непер |A(x)|, то досягає свого inf у т. х⁽⁰⁾.

| х⁽⁰⁾| =1; |A(х⁽⁰⁾)| = inf |A(x)|.

В силу додотньої визначеності |A(х⁽⁰⁾)| >0.

Лема 2. Якщо А(х) – кВ. форма, x⁽⁰⁾ ≠0, то х прямої k = tx⁽⁰⁾ , t≠0 викон:

,

Теорема (достатні умови екстремума). Нехай ф-я f(x) двічі неперервно диференційовна в околі деякої критичної точки x⁽⁰⁾. Тоді якщо другий диференціал ф-ї в цій точці d² = f (x⁽⁰⁾) додатньо визначена (від’ємно) квадр форма, то x⁽⁰⁾ – точка строгого локального min(max). Якщо d² = f (x⁽⁰⁾) знакозмінна квадр форма, то в точці x⁽⁰⁾ немає екстремума.

Заув: (критерій Сільвестра): - Якщо усі кутові мінори матриці кв форми додатні, то кв форма – додатньовизначена.

- Якщо кутові мінори кв форми змін. знак, починаючи з від’ємного, то кВ форма від’ємно визначена.

Доведення: Застосуємо формулу Тейлора для f(x) у т. x⁽⁰⁾ і запишемо до другого порядку:

,

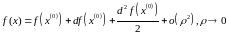
1) А(∆х) – знако визначена кв форма → inf|A(∆x)| > 0 → 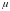= inf|A(∆x)| > 0

, inf | A( )| = > 0 > 0 : х є Rⁿ : |∆x| < :

Отже, у (A( )+2 головним є 1-й доданок, а 2-й завжди менший за 1-й.

Якщо 2 диф. додатньо визнач кв форм. ,то 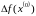>0 → - строгий локальн min.

Якщо 2 диф. від’ємно визнач кв форм. ,→ - строгий локальн mах.

2) А(∆х) – знако змінна кв форма. х^/, х^// є

A( ) > 0, A( ) < 0 > 0

∆x=t∆x^/

∆x=t∆x^//

Отже, приріст ф-ї змінює знак, тому - не є точкою локального екстремума!!!