66. Заміна змінних у потрійних інтегралах. Перехід від декартових координат до циліндричних і сферичних координат.

Нехай в декартовый системі координат задана область V-компакт, а на ній задано -неперервна. Також маємо

, координати

Припустимо, що x(.), y(.), z(.) – непер., непер.-диференц. та однозначні на , тоді має місце формула заміни змінних в потрійному інтегралі

Частинні випадки

1. Потрійний інтеграл в циліндричній системі координат

Циліндричні координати т. М – це полярні координати проекції т. М на площину xOy та апліката т. М в декартовій системі координат.

Формули переходу:

, , тобто маємо

2. Потрійний інтеграл в сферичній системі координат.

Сферичні координати т. М – це модуль радіус-вектора т. М, кут між Oz і радіус-вектором т., полярний кут проекції т. М на площину xOy.

Формули переходу:

, тобто маємо

Застосування потрійного інтегралу:

1. Об’єм тіла

2. Маса речовини в об’ємі просторова щільність речовини.

67. Означення криволінійних інтегралів першого та другого роду, їх основні властивості та обчислення.

К.І. першого роду

Нехай площа XOY задана обмеж. Кривими

L=(AB).

Задача

Ф-ія f(x,y), -непер.Розіб’ємо криву на дуги точками , і=

Позначимо -довжина дуги . Вибираємо .

Складемо інтегральну суму: . Позн.

Якщо, існує скінчена границя інтегр. Сум при і залежить від способу розбиття кривої на частини і вибору m, , то ця границя назив. Криволінійним інтегралом 1 роду від скалярної ф-ії f(x,y) по дузі (кривій) L.

Властивості:

1)

2)Адитивність по кривій

;

Обчислення:

1)Нехай L задана параметрично

x(t) і y(t) – непер. диференц. на

2)

y(x)-неп.диференц.

3) Полярна сис-ма координат

; - неп. дифер.

К.І. другого роду

Нехай на площ. задана крива L=(AB). У кожній m кривої задана векторна ф-ія . Розбиваємо криву на частини m, , і=

; ;

Якщо, існує скінчена границя інтегральних сум при та не залежить від способу розбиття L на частини, то ця назив. Криволінійним інтегралом 2 роду від векторної ф-ії по кривій L.

Нехай має координати ;

Властивості:

1. 

2. 2 та 3 див. попередні

Обчислення:

1)

2)

68. Означення поверхневих інтегралів першого та другого роду, їх властивості та обчислення. Поверхневі інтеграли другого роду

Нехай пряма перетинає поверхню тільки в одній точці і нехай проекція поверхні на . Нехай на поверхні задано векторну функцію:

- площа поверхні

- орт нормалі до поверхні в точці

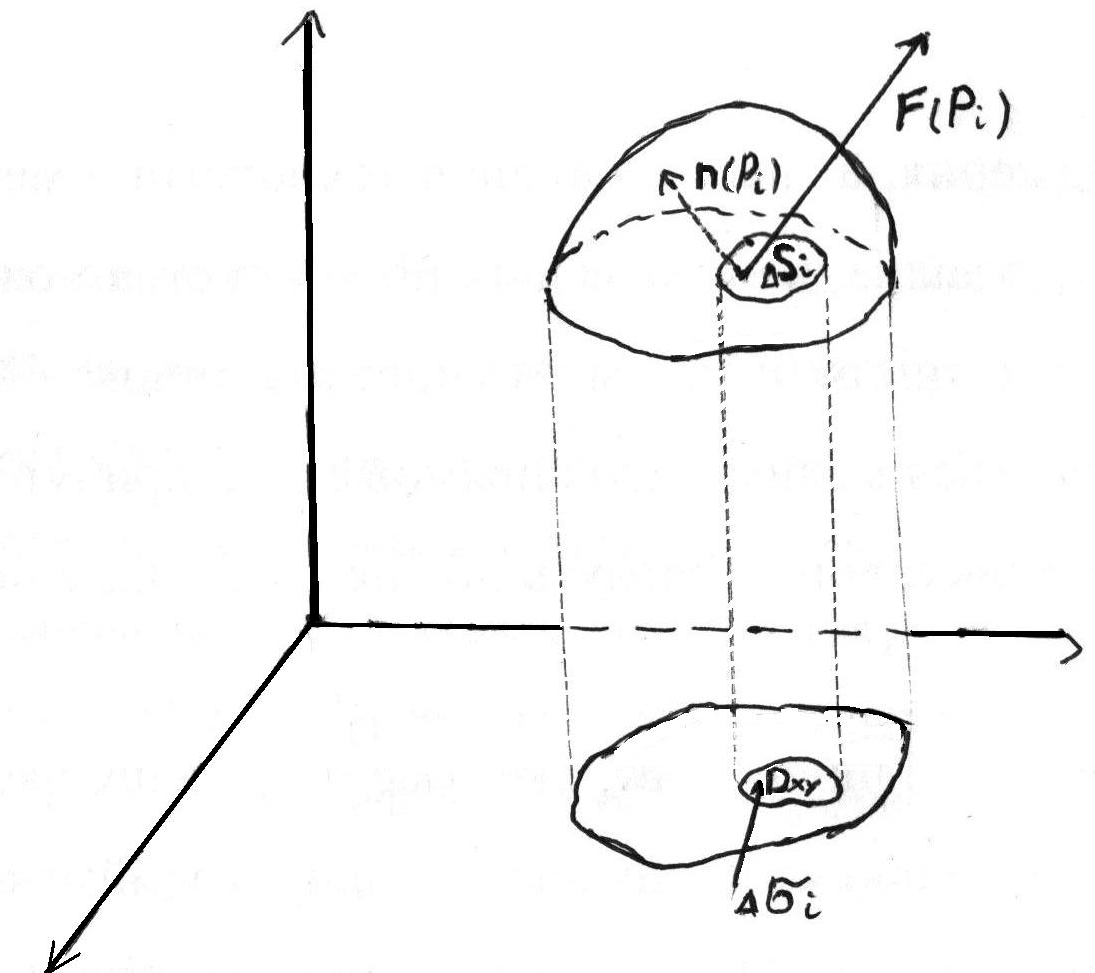
Якщо існує скінченна границя інтегральних сум при та не залежить від способу розбиття поверхні на частини і вибору точок , то ця границя називається поверхневим інтегралом другого роду від векторної функції по поверхні .

Припустимо . Тоді

Зауваження:

Обчислення інтеграла:

Оскільки та

Варто зазначити, що знак вибирається за таким принципом: Якщо кут між вектором нормалі і віссю - гострий, то беремо +, якщо тупий – то -.

Остаточно:

Знаки відповідних інтегралів вибираємо відповідно до знаку відповідного косинуса.

Отже, цей інтеграл зводиться до трьох подвійних інтегралів.