1. Визначення вимірного простору.

_{Озн. 1. Множина всіх впорядкованих систем вигляду 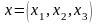; 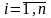для яких введено лінійні комбінації та скалярний добуток називається n-вимірним арифметичним евклідовим векторним простором.}

_{Позначення:}

_{- нуль-вектор. - обернений вектор.}

_{Властивості скалярного добутка (за озн.)}

1. Симетричність

2. _{Лінійність}

3. 

4. 

_{Властивості}

1. 

2. 

3. _{Нерівність Коші-Шварца (1)}

_{Доведення: - виконується.}

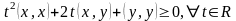
_{Наслідок 1: (2),}

_{Наслідок 2: (3)}

_{Зауваження: Нерівності (1), (2), (3) в координатній формі:}

1. 

2. 

3. 

_{Означення:} Відстанню між векторами _{називається число}

_{Означення 2: Множина всіх впорядкованих систем для яких введено поняття відстані називається n-вимірним точковм арифметичним евклідовим простром.}

_{Позначення:}

_{- початок координат}

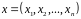_{- точка простору}

_{Властивості відстані}

1. 

2. 

3. Симетричність

4. 

Зауваження: Введений точковий простір є прикладом метричного простору.

Метричний простір – це пара _{де - довільна не порожня множина, - це метрика (числова функція, яка задовольняє властивостям 1-4).}

2. Збіжність послідовностей точок в вимірному просторі.

_Нехай

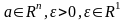
_{Означення}

_{околом точки (кульовим околом т. а / відкритою кулею радіуса з центром в т. ) називається множина}

_{Означення: Послідовністю точок в просторі називається відображення}

_{послідовність точок в}

_{Підпослідовність основної послідовності}

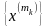
_{Означення: Точка називається границею послідовності якщо}

_{Позначення:}

_{Означення’:}

_{Теорема (Критерій збіжності в /по координатна збіжність):}

_{Доведення спирається на нерівність, яка доводиться піднесенням до квадрату}

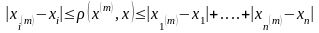
_{Властивості границі послідовності в аналогічні в випадку}

_{Означення: Множина в називається обмеженою, якщо вона міститься в деякому n-вимірному кубі}

_{Зауваження: Будь-яка куля містить куб та сама міститься в деякому кубі.}

_{Означення: послідовність точок в називається обмеженою, якщо множина її значень обмежена.}

_{Теорема Больцано-Веєрштраса: З будь-якої обмеженої послідовності точок можна виділити збіжну підпослідовність.}

_{Доведення: Нехай послідовність точок 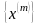обмежена. Отже множина її значень міститься в кубі.}

_{обмежені}

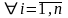
_{За теоремою Больцано-Веєрштрасе збіжна}

_збіжні

_{За критерієм збіжності}

_{Околом нескінченно віддаленої точки називається множина}

_{Кажуть, що послідовність прямує до , коли}

3. Різні типи множин в вимірному просторі.

Точка множини назив.її внутрішньою точкою,якщо вона міститься в цій множині разом з деяким своїм околом.

Множина всіх внутрішніх точок множини 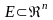назив.її внутрішністю.

Позначимо : . Множина,у якої всі точки є внутрішніми назив.відкритою

( ). Лема: круговий окіл є відкритою множиною.

Точка простору 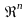назив. точкою дотикання множини Е,якщо будь-який її окіл містить точки множини Е.

Теорема: т. є точкою дотикання множини .

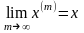Точка простору назив. граничною (предельной) точкою множ. Е, якщо в будь-якому її околі містяться точки множ. Е ,відмінні від неї самої.

т. назив. ізольованою точкою множ. Е,якщо будь-який окіл цієї точки не містить інших точок Е, крім самої х.

Будь-яка точка дотикання множини Е є або граничною,або ізольованою. Множина всіх точок дотикання множини Е назив. її замиканням. Позначення:

Множина,яка містить всі свої точки дотикання, назив. замкненою.

Теорема: з будь-якої послідовності точок компакту (замкнена обмежена множина) можна виділити збіжну до його точки підпослідовність.

Точка простору назив. межевою(граничной) точкою множини Е,якщо будь-який її окіл містить як точки множини Е,так і точки,що не належать Е.

Множина межевих точок назив. межею. Позначення: .

Кривою в просторі назив. неперервне відображення відрізка в просторі

Т=

Множина Е назив. лінійнозв’язною, якщо будь-які дві її точки можна сполучити кривою в цій множині.