23. Истечение газов из отверстий.

Рассмотрим истечение газа из резервуара через небольшое отверстие при поддержании в резервуаре постоянного давления. Рассмотрим следующую схему:Пусть внутри сосуда р₁; плотность ρ₁; температура Т₁ (сечение 1-1), а на выходе в сечение 2-2 соответственно р₂, ρ₂, Т₂. Будем считать скорость на входе υ₁=0, а на выходе υ₂. Процесс истечение газа с термодинамической точки можно считать адиабатическим т.к. на весьма коротком пути от резервуара до сечения 2-2 влияние теплообмена между выходящим газом и внешним пространством можно пренебречь. Запишем уравнение Бернулли при адиабатическом процессе для сечений 1-1 и 2-2 временно пренебрегая потерями энергииz₁+ = z₂+ - , где k – адиабатическая постоянная газа. k= , где С_р –теплоемкость газа при постоянном давлении. - теплоемкость газа при постоянном объеме. Т.о. этим показателем учитывается сжимаемость газа. Е₀=k*p. Пренебрегая геометрическими высотами и скоростью подхода уравнение Бернулли примет вид: , выразим отсюда скорость : . Это выражение носит название ур-ния Сен-Венана для скорости истечения газа. Преобразовав это выражения можно найти значения выражений р₁ и р₂: =1- , р₂= р₁ имеем в ввиду что отношение k* =C₁², где C₁² – скорость распространения звука в покоящемся газе. Можно получить выражение скорости вытекания газа из сосуда: = , во всех случаях когда отношение значительно меньше 1 т.е. при , то этим отношением можно пренебречь и тогда скорость истечения равна: = т.е. та же формула что и для капельной жидкости (υ=). Максимально возможная скорость истечения газа будет при р₂=0: = . Массовый расход вытекающего газа(пренебрегая сжатием струи) равен: М= , где ω – площадь сечения отверстия. Влияние сжатия струи на подходе к отверстию и др. неучтенных факторов учитывается как и при истечении несжимаемой жидкости введением коэффициента μ т.е. М= .

24. Относительное движение тела и жидкости. Общие сведения.

Движение твердых тел в жидкости (обтекание жидкостью твердых тел) представляет одну из важнейших проблем гидромеханики. Основной задачей при этом является определение сил, которые возникают при относительном движении тела и жидкости. Тело движущейся жидкости встречает со стороны последней сопротивление, для преодоления которого необходимо преодолеть некоторую силу. В случае когда тело неподвижно, а жидкость обтекает его - наоборот тело оказывает сопротивление движению жидкости, на преодоление которого тратится энергия. Рассмотрим случай обтекания потоком жидкости пластинки установленной перпендикулярно скорости потока.

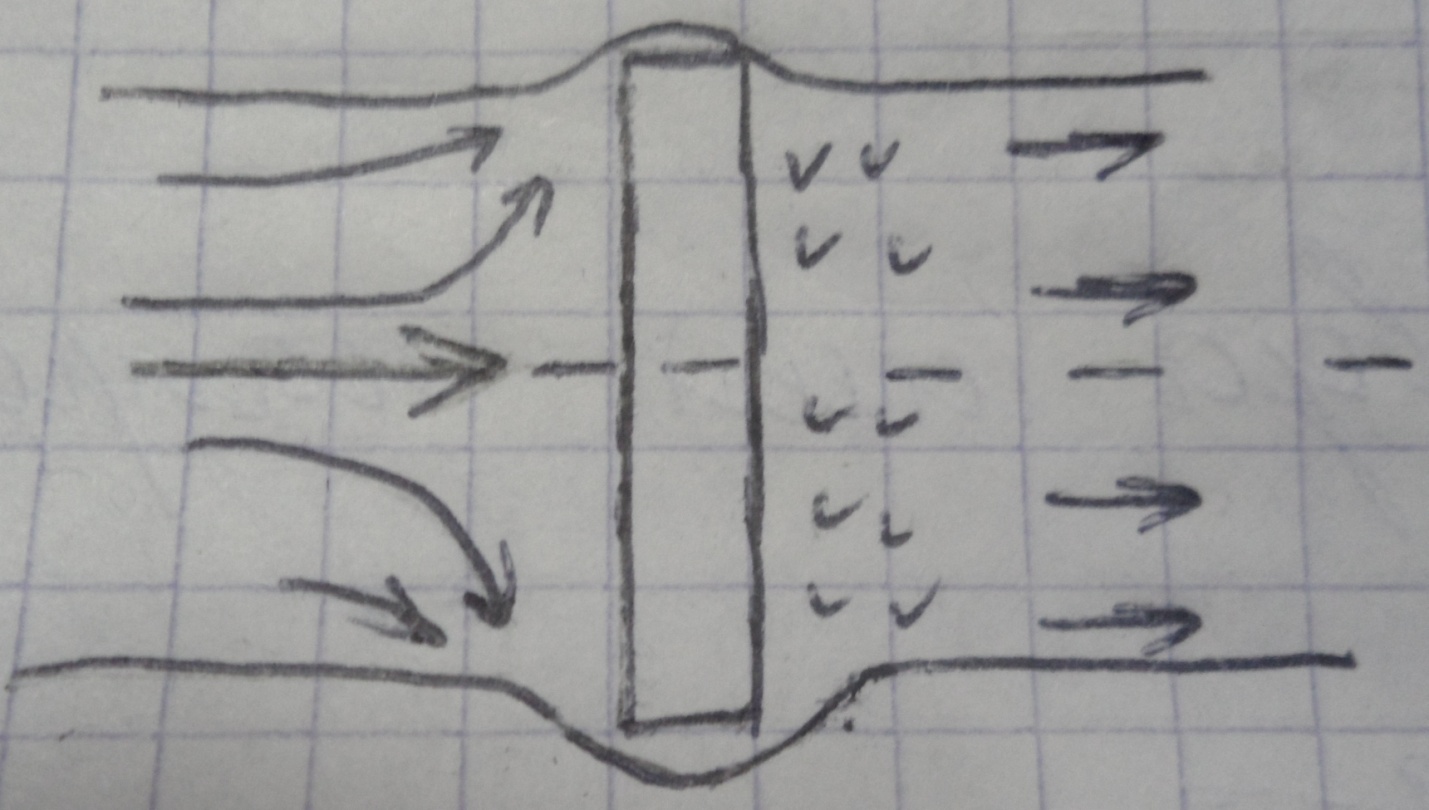Струйки жидкости встречаясь с пластинкой, оказывают дополнительное давление, обусловленное изменением направления течения на поверхность, обращенную навстречу потоку. Со стороны пластинки на жидкость действует сила сопротивления, равная по величине добавочной силе давления на пластинку. Непосредственно за пластинкой в результате отрыва струи от пластинки образуется область беспорядочного вихревого движения, в этой области давление понижено. В результате чего возникает дополнительная сила сопротивления, также направленная навстречу потоку. Поскольку эта сила зависит от формы тела, её называют сопротивлением формы. Сумма обоих указанных сопротивлений называют сопротивлением давления. Если пластинка расположена вдоль потока, оказываемое ею сопротивление вызывается главным образом тангенциальными силами трения, возникающего на боковых поверхностях пластинки(т.н. сопротивление трения). Сопротивления давления и трения чаще все существуют одновременно. И полное сопротивление F, которое возникает при относительном движении тела и жидкости, представляет собой сумму этих сопротивлений. F=F_{давления} +F_трения. Соотношение между компонентами полного сопротивления в различных случаях различно(пластинки расположенные вдоль или поперек потока являются предельными случаями). Полное сопротивление F было определено еще Ньютоном в виде: F=C*ω*ρ*(υ²/2), где С – коэффициент сопротивления, обычно определяемый из опытов. ω – характерная площадь тела. ρ – плотность жидкости. υ – характерная скорость.