16. Истечение жидкости из малого отверстия в тонкой плоской стенке при постоянном напоре в атмосферу.

С.328

Малым отверстием называют отверстие,когда d<0.1H.

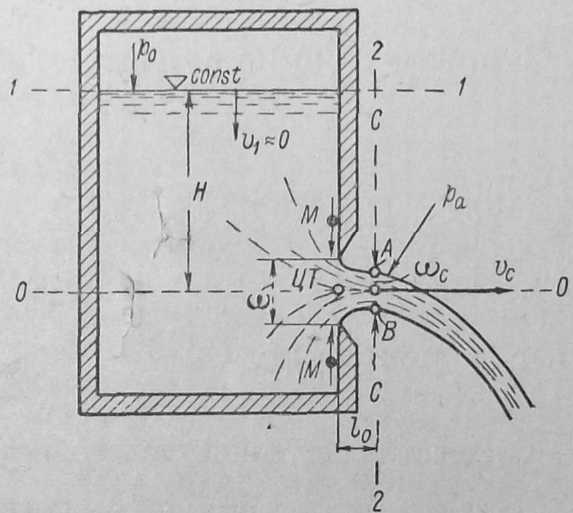
Как показывают опыты, картина истечения жидкости из некоторого сосуда через малое отверстие в вертикальной тонкой стенке имеет вид, изо­браженный на рис.1, где обозначено:

р₀ — давление на поверхности жидкости в сосуде; в общем случае p₀ не равно атмосферному давлению р_а; ω— площадь отверстия; ω_с — пло­щадь сечения струи в некотором сечении С—С, называемом сжатым сече­нием; H — заглубление центра тяжести площади ω отверстия под уровнем жидкости в сосуде; падением жидкости на расстоянии l₀ от стенки сосуда до сжатого сечения пренебрегаем, а поэтому считаем, что Н является также заглублением центра тяжести площади ω_с под уровнем жидкости в сосуде.

Струя жидкости по выходе из отверстия резко сжимается на протяжении до сечения С—С. Такое сжатие обусловливается инерцией частиц жидкости, движущихся при подходе к отверстию по криволинейным траекториям [в частности, инерцией частиц М, которые скользят непосредственно по стенке сосуда и, выйдя из него, движутся по границам струи].

Если не учитывать возможной аэрации струи, т. е. насыщения ее пузырьками воздуха, а также не учитывать сопротивления воздуха, то надо считать, что за сжатым сечением С—С, в связи с увеличением скорости падающей жидкости, струя должна продолжать сжиматься, но относительно слабо. Сжатое сечение С—С является тем первым (по течению) сечением, к которому можно прилагать уравнение Бернулли; к сечениям струи левее линии С—С уравнение Бернулли неприменимо, так как движение здесь резко изменяющееся.

Если отверстие круглое, то расстояние от внутренней поверхности стенки до сжатого сечения, согласно имеющимся опытам, будет: l₀≈0,5d. где D — диаметр отверстия. Введем обозначение: ω_с / ω=ε,величина ε называется коэф-том сжатия струи. Найдем среднюю скорость v_c в сжатом сечении и расход Q жидкости, вытекающей из сосуда. Для решения этой задачи соединяем уравнением Бернулли два сечения: 1—1 и 2—2, из которых первое намечаем на уровне жидкости в сосуде и второе — по ли­нии С—С. Плоскость сравнения 00 про­ведем] на уровне центра тяжести площади ω_с.

Уравнение Бернулли в известных нам обозначениях имеет вид:

z₁=H, p₁/γ= p₀/γ, αv²₁/2g≈0, z₂=0, p₂/γ= p_a/γ, αv²₂/2g≈ v²₂/2g= v²_c/2g,

z₁+(p₁/γ) +(αv²₁/2g)= z₂+ (p₂/γ) +(αv²₂/2g)+hf.

Скоростью движения жидкости в сосуде пренебрегаем. Подчеркнем, что давление в жидкости в сечении С—С равно атмосферному. Величину потерь напора от сечения1—1 до сечения 2—2 представим формулой:

h_f=ζ_f *v²_c/2g, где ζ_f — коэффициент сопротивления, учитывающий потери напора от сечения 1—1 до сечения 2—2.

H+p₀/γ= p_a/γ+ v²_c/2g+ ζ v²_c/2g,

H+(p₀/γ -p_a/γ)=H_пр

где H_пр можно назвать приведенным напором.

v_с=√1/(1+ζ)√2gH_пр, v_с= φ √2gH_пр, φ=√1/(1+ζ),

v_с=√2gH_пр Эта формула называется формулой Торричелли.

Определим расход:

Q=ω_с v_с= ω_с φ √2gH, Q=ε ω φ √2gH, Q=μ₀ ω √2gH,где μ₀= ε φ.

причем здесь μ₀ называется коэффициентом расхода отверстия.