13 Расчетные зависимости для величины гидравлического удара и скорости его распространения.

П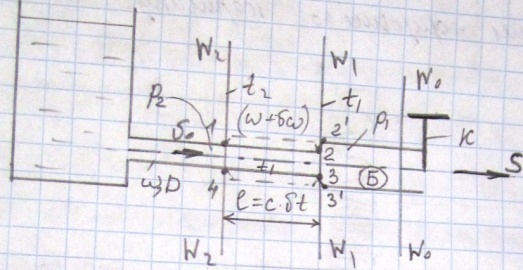 редставим на рисунке цилиндрический трубопровод Т, на в конце которого имеется частично открытый кран К. Будем считать, что в трубопроводе сечении W₀—W₀, намеченном у крана, скорость движения жидкости = v₀.

Представим себе далее, что в момент времени t=0 открытие крана К мгновенно изменилось, в связи с чем скорость в сечении W₀—W₀ мгновенно изменилась (например, уменьшилась) на величину δv, у крана зародилась область возмущения Б.

Будем считать, что в некоторый момент времени t₁ граница области возмущения занимает положение W₁—W₁. в некоторый момент t₂ = t₁ + δt эта граница переместится в положение W₂—W₂ Расстояние между вертикалями. W₁—W₁ и W₂—W₂ равно l=c*δt, за время δt стенки трубы на длине l раздадутся и примут положение, показанное на чертеже штриховой линией.

h

Применив к отсеку жидкости W₁—W₂, заключенному между сечениями W₁—W₁ и W₂—W₂ уравнение неразрывности и теорему количества движения, получаем следующие расчетные зависимости:

а) Зависимость для величины h_уд: h_уд=(р_уд/ϒ)=-(с/g)*δv, где δv- положительное или отрицательное приращение (во времени) ско­рости движения жидкости.

Тогда величина гидравлического удара равна

б)Зависимость для величины с (в случае круглой трубы):

с-скорость распространения ударной волны

где Е_ж — модуль объемной упругости жидкости; Е_т — модуль упругости материала стенок трубы; D — внутренний диаметр трубы; е — толщина стенок трубы. Введем обозначения - скорость распространенна звука в покоящейся жидкости, для воды с ₀ = 1425 м/сек.

(9-55)

Учитывая это, выражение для относительной скорости распространения гидравлического удара в круглой тонкостенной трубе, заполненной водой, можно окончательно представить в виде: ,м/сек,

Надо заметить, что величина с может измеряться сотнями и даже тысячами метров в секунду.

14, Прямой (начальный) и отраженный гидравлические удары.

П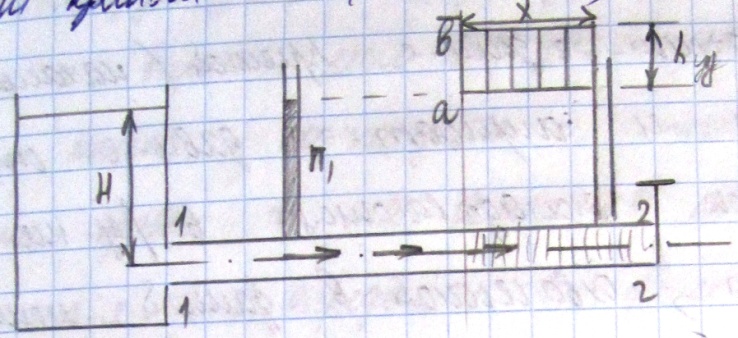 редставление о гидравлическом ударе будет неполным, если мы не учтем еще следующего существенного обстоятельства.Представим трубу, заполненную жидкостью; один конец трубы открыт (сечение 1-1), другой конец прикрывается краном К (сечение 2—2).

К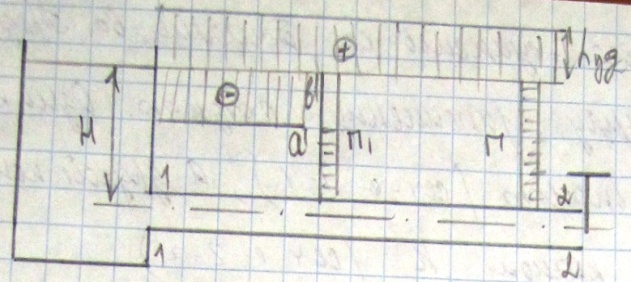 ак уже известно, в случае мгновенного закрытия крана в жидкости зарождается волна положительного давления, имеющая вертикальный «лоб» ab, причем эта волна движется вдоль трубы.

Как только «лоб» указанной положительной волны доходит до открытого конца трубы, (в сечении 1—1) возникает отраженная отрицательная волна, представляющая собой зеркальное отображение прямой волны, повернутое на 180°. «Лоб» а'Ь' отраженной отрицательной волны движется с той же скоростью с в сторону, противоположную положительной волне.

положительные давления прямой (начальной) волны и отрицательные давления отраженной волны складываются; в результате на участке трубы охваченном в данный момент времени отраженной волной, давление, обусловленное гидравлическим ударом=0. Как только «лоб» указанной отрицательной волны доходит до закрытого конца трубы, в этом месте (в Сечении 2—2) возникает отраженная отрицательная волна, со скоростью с в сторону, противоположную той отрицательной волне, которая подошла к сечению 2—2. У открытого конца трубы 1—1 всегда зарождаются отраженные волны обратного знака (по отношению к прямым волнам, подошедшим к этому концу); у закрытого же конца трубы 2—2 всегда зарождаются отраженные волны того оке знака, что и прямые волны, подошедшие к этому концу.Обозначим через t₀ время пробега «лба» волны аЬ от сече­ния 2—2 до сечения 1-1: ,где L — длина трубы. Пользуясь этим обозначением укажем следующее:

а) в момент = t₀ времени, отсчитываемого от момента закрытия крана, по всей длине трубы давление должно быть одинаковым ;

б) в момент времени = 2t₀ давление по всей длине трубы должно быть равным нулю .

в) в момент времени = 3t₀ давление по всей длине трубы должно быть равным ;

г) в момент времени t₄ = 4t₀ давление по всей длине трубы должно быть равным нулю,

Таким образом, полный период t_n колебания давления в любом неподвижном поперечном сечении трубы будет равен четырехкратному времени пробега «лбом» волны расстояния L: Если наметим на трубе неподвижное сечение, то давление в этом сечении будет изменяться во времени. В реальных условиях указанное колебание величины давления должно постепенно затухать.

15 Случай постепенного закрытия крана. Полный и неполный гидравлические удары.

Положим, что мы имеем истечение в атмосферу из весьма длинной горизонтальной трубы Т, присоединенной к сосуду Б.(рис а) Будем считать, что кран К, установленный в конце трубы, закрывается не мгновенно, а так, что скорость v_кн в самом конце трубы(перед краном) уменьшается,например , по линейному закону от v_KH = v₀ до v_KH = 0,(рис.б), где v₀ — скорость в трубе при установившемся движении, когда кран полностью открыт.

О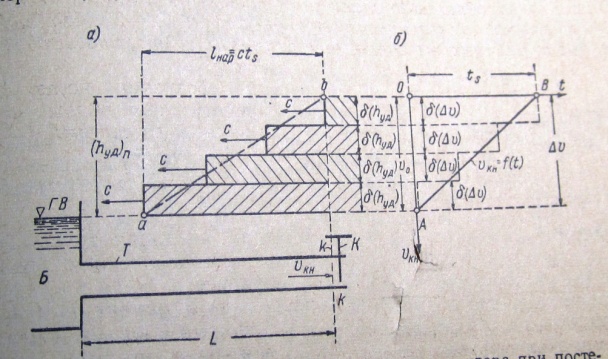 бозначим время полного закрытия крана через t_s. В момент t_s, отсчитываемый от начала закрытия крана, скорость в конце трубы уменьшается на величину Δv=v₀ и становится равной нулю. Представим себе, что скорость v_KH уменьшается по графику в виде ступенчатой линии (на рис.б штриховой линией), причем высоту каждой намеченной достаточно малой ступени обозначим через δ(Δv). Уменьшая скорость v_KH на элементарную величину δ(Δv) будем посылать в трубу элементарный гидравлический удар, δ(h_уд)=(c/g)δ(Δv) . В момент времени t_s, когда в трубу будет послан последний элементарный удар δ(Δv) будем иметь ступенчатый график волны повышения давления, показанный штриховкой на рис.а.) В данном случае назовем полным ударом (h_УД)_П величину (h_УД)_П=(c/g)v₀.

Из графика на рис. а видно следующее:

а) в момент t_s полного закрытия крана в конце трубы (у крана) получается полный гидравлический удар (h_УД)_П величина которого в этом месте сохраняется на протяжении последующего времени;

б) длина нарастания полного удара, т. е. длина графика волны, на протяжении которой давление возрастает от нудя до(h_УД)_П ,l_нар=сt_s.

Будем теперь уменьшать высоту ступени δ(Δv) (рис. б) до нуля т. е. приближать ступенчатый график к прямой линии АВ.

Следует запомнить, что при постепенном закрытии крана, когда скорость v_кн в конце трубы уменьшается по линейному закону, имеем следующее:

а) «лоб» волны оказывается очерченным наклонной прямой аЬ.

б) длина нарастания полного удара получается равной l_нар=сt_s.

в)полный удар в конце трубы наступает в момент t_s (когда кран полностью закрывается), причём эта величина удара сохраняется в дальнейшем.

Выше мы рассмотрели длинную трубу, для которой всегда получается полный удар. Имея в виду теперь трубу любой длины, будем различать при постепенном закры­тии крана два разных случая: 1) полного гидравлического удара; 2) неполного гидравлического удара.

Чтобы пояснить вопрос о неполном ударе, обратимся к рис.2. При постепенном закрытии крана К, когда положительная волна давления отражается от жидкости в сосуде, мы получаем отрицательную отраженную волну. Если длина нарастания полного удара l_нар оказывается большей, чем удвоенная длина L трубы, то гидравлический удар у крана К в процессе его закрытия, постепенно нарастая, но еще не достигнув своей полной величины, в некоторый момент времени перестает увеличиваться благодаря тому, что отрицательная отраженная волна, успев подойти к крану до момента его полного закрытия, начинает накла­дываться в этом месте на положительную волну.

Можно сказать, что

1)полным гидравлическим ударом называется наибольшая величина постепенно нарастающего прямого гидравлического удара, не сниженная отраженным ударом (имеющим другой знак и не успевшим дойти до места зарождения данного прямого удара к моменту завершения его роста);

2)неполным гидравлическим ударом называется наибольшая величина гидравлического удара, получающаяся в месте зарождения прямого (начального) удара при условии, когда отраженный удар успевает прийти к указанному месту раньше, чем постепенно нарастающий прямой удар достигнет полной своей величины.

Величина полного гидравлического удара выражается формулой .

У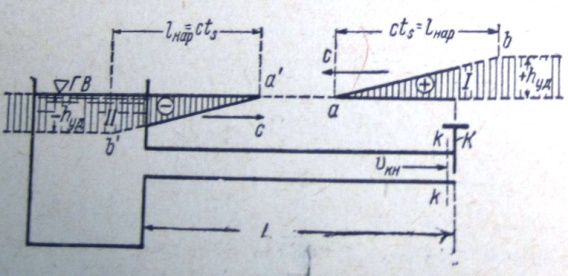 словие, при котором получается неполный удар .>2L и записывается формулой

Из этой формулы видно, что стремясь уменьшить давление жидкости в трубопроводе, следует увеличивать время закрытия крана t_s и уменьшать длину рассматриваемого напорного трубопровода L.