7. Длинные трубопроводы. Истечение под уровень и в атмосферу.

Рассмотрим 2 случая:

1.истечение под уровень из длинных трубопроводов.

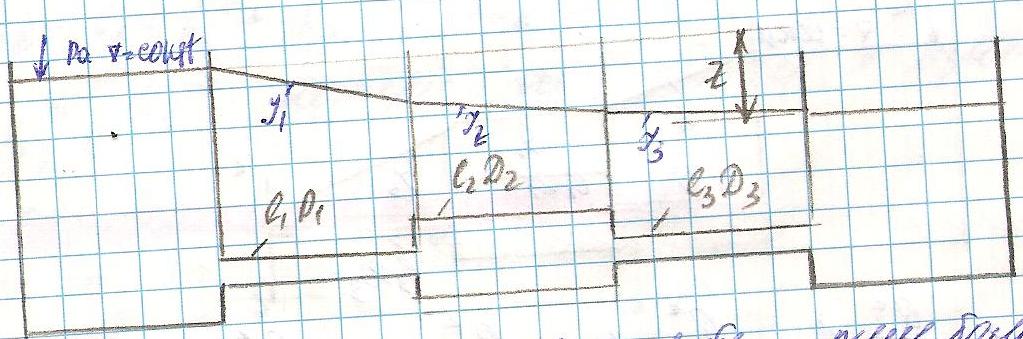
Чем больше скорость в трубе, тем больше потери напора, а следовательно и величина I. Поэтому при пьезометрический уклон должен быть больше пьезометрического уклона . Разность горизонтов жидкости в сосудах z при истечении под уровень равен потери напора, т.е

Где соответственно потери напора по длине в 1-ой, 2-ой и 3-ей трубах.

В длинных трубах потери напора по длине определяются по формуле:

Где - расходная характеристика, определяемая по специальным таблицам в зависимости от диаметра труб.

1.истечение в атмосферу.

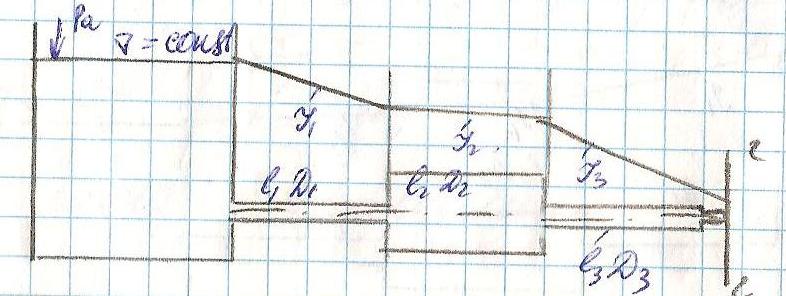
µ- коэффициент расхода насадки, определяющийся по специальным таблицам.

ω – площадь живого сечения насадки.

8. Последовательное и параллельное соединение труб.

Последовательное соединение.

При последовательном соединении потеря напора суммируется по участкам труб от сечения А до В.

, - потери по длине в трубе 1, 2, 3.

Параллельное соединение труб.

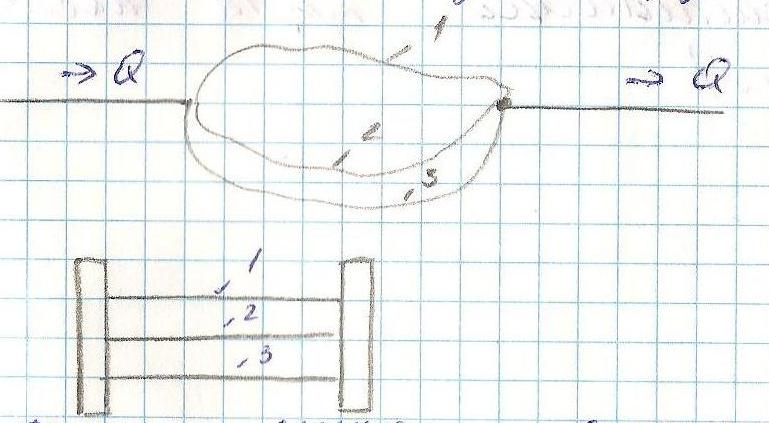
В этом случае складывать потери нельзя.

Рассмотрим следующую схему.

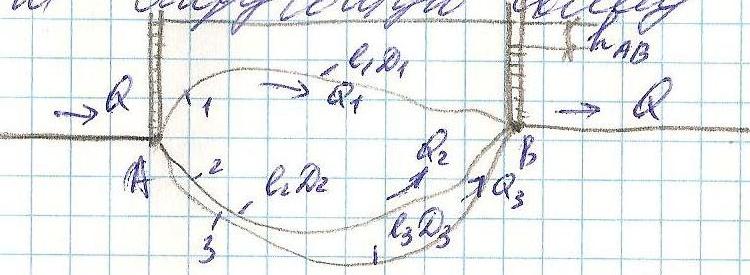
Как видно потери напора во всех трубах соединенных параллельно одинаковы. Для потерь напора по длине при параллельном соединении можно записать:

=

12, Неустановившееся напорное движение жидкости. Гидравлический удар с учетом сжимаемости жидкости и упругими стенками трубопровода. Предварительные указания.

Будем рассматр напорное движение жидкости в случае когда учитывается ее сжимаемость, причем стенки трубопровода считаются неабсолютно жесткими( упругими, деформирующимися.) Гидравлическим ударом называется повышение или понижение гидромеханического давления в напорном трубопроводе, вызванное изменением во времени (в каком-либо сечении трубопровода) средней скорости движения жидкости. Явление гидравлического удара обусловливается инерцией той массы жидкости, заключенной в трубопроводе, скорость которой изменяется во времени. Гидравлический удар в трубопроводе может достигать большой силы.. Поэтому при расчете толщины стенок трубопроводов приходится учитывать величину гидравлического удара. Положим, что мы имеем трубу, на конце которой установлен кран , Жидкость, находящаяся в трубе, будучи остановлена закрытием крана, благодаря своей инерции окажет большое давление на закрытый кран.Если при рассмотрении такого явления пренебрежем сжимаемостью жидкости и деформируемостью стенок трубы, то при этом получим в трубе так называемый «абсолютно жесткий»,удар что, как показывает опыт, вовсе не отвечает действительности. На характер явления гидравлического удара оказывают большое влияние сжимаемость жидкости и деформируемостью стенок трубопровода. Благодаря этим обстоятельствам в трубопроводе при закрытии или открытии крана получается упругий удар, В случае упругого удара давление вдоль трубопровода распространяется волнами, причем эти волновые явления оказываются весьма резко выраженными, и с ними необходимо считаться.

О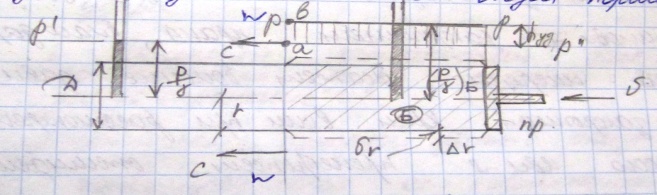 писание явления гидравлического удара.

Представим горизонтальную трубу Т, наполненную жидкостью, и в нее введен поршень П_р.

Если жидкость и поршень неподвижны, то при этом в жидкости всюду будет некоторое давление, определяемое горизонтальной пьезометрической линией Р'-Р". Если представить, что поршень в некоторый момент t = 0 начал мгновенно двигаться со скоростью v , то в случае абсолютно несжимаемой жидкости и абсолютно жестких стенок трубопровода, жидкость также начнет двигаться с той же скоростью v по всей длине трубопровода. Если жидкость сжимается и упругие стенки трубопровода, картина другая. В этом случае поршень П_р, приведенный в движение, будет выводить жидкость, находящуюся в трубе , из состояния покоя постепенно. Такое положение обусловливается, с одной стороны, сжимаемостью жидкости и упругостью стенки трубопровода и, с другой, наличием сил инерции жидкости. Для некоторого момента времени t` (после начала движения поршня) будем иметь граничную вертикаль W—W, которая разделяет жидкость, заполняющую трубу, на два разных объема: а) объем левее вертикали W—W; здесь жидкость находится еще в состоянии покоя, и давление в этой жидкости то же, что было до начала движения поршня, т. е. равное ;

б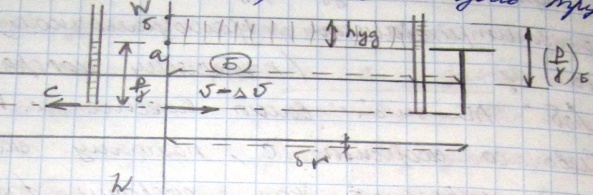 ) объем правее вертикали W—W; здесь жидкость находится уже в состоянии движения. причём, скорость движения жидкости в любом живом сечении v= скорости движения поршня. По мере движения поршня влево со скоростью v, вертикаль W—W движется влево со скоростью с, причем с значительно большей v. Область жидкости Б, можно назвать зоной возмущения или зоной упругой деформации жидкости; скорость с — скоростью распространения возмущения или скоростью распространения упругой деформации жидкости.Как видно из соотношения c>>v длина области возмущения Б с течением времени должна расти: расстояние между поршнем и границей W—W должно изменяться от 0 до сколь угодно большой величины.Зона возмущения Б имеющая подвижную границу W—W_t характеризуется следующими обстоятельствами:

1) гидродинамическое давление внутри этой зоны оказывается всюду повышенным на величину, измеряемую высотой h_уд: ; где, - пьезометрическая высота ,соответствуящая области Б, -пьезометрическая высота до начала движения поршня.

Эпюра h_уд- вертикально заштрихованный прямоугольник, выражающий волну повышения давления. «Лоб» ab этой волны вместе с вертикалью W_W движется влево со скоростью с, Поэтому скорость с можно рассматривать, как скорость распространения в трубопроводе повышенного давления;

2) в зоне возмущения Б, сжатие жидкости оказывается относительно большим (повышается плотность), а упругие стенки трубопровода раздавшимися на некоторую величину r.

Описанная картина получается при движении поршня в трубе, наполненной покоящейся жидкостью. Совершенно тождественная картина получается в случае, когда жидкость движется в трубе со скоростью v, причем в некоторый момент времени t = 0 мы мгновенно перекрываем данную трубу задвижкой. Здесь в момент t=0 у задвижки зарождается зона возмущения Б, и граница W—W этой зоны начинает перемещаться со скоростью v вдоль трубы. Такой случай возможен при полностью закрытой задвижки. На этом чертеже изображено частичное прикрытие задвижки, когда скорость v в конце трубы уменьшается не до нуля, а до величины, равной .

В случае открытия задвижки, когда скорость получается равной . Картина такая же ,однако труба в этом случае сжимается здесь возникает волна понижения давления и скорость ее распространения с.При рассмотрении гидравлического удара полезно иметь в виду следующую аналогию. Представим себе обычную спиральную пружину, имеющую большую длину. Пусть эта пружина падает вертикально вниз . после того как пружина коснулась, горизонтальной плоскости, получим картину.

явление гидравлического удара характеризуется двумя основными величинами: 1,приращением давления h_уд («+» или «-»), дающим величину гидравлического удара;

2,скоростью с распространения возмущений, т. е. скоростью распространения гидравлического удара . определяем эти величины