36. Понятия о подобии гидравлических явлений.

Представим себе 2 геометрически подобных фигуры. Условимся сходственными точками 2 этих фигур называть точки, одинаково расположены по отношению к границам этих фигур.

Физически подобными наз-ся явления одной и той же физической природы. Для которых все характернее величины подобны: в сходственных точках натуры и модели и в соответственные моменты времени для подобных явлений все векторные величины должны быть геометрически подобными, а скалярные – соответственно пропорциональными.

При физич. моделировании гидравлических явлений с использованием материальных моделей, удобно различать геометрическое, кинематическое и динамическое подобия.

1. Геом. подобие.

Две гидравлические системы будут подобными в том случае если м/д сходственными размерами этих систем всюду существует постоянное соотношение:

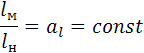
Где l_н- размер натуры,

L_м-размер модели,

A – масштаб.

Для геометрически подобных систем

Где w_н,V_н – площадь и объём натуры.

W_м,V_м – площадь и объём модели.

2. Кинематич. подобие.

Две гидравлические системы будут подобными в том случае если:

а) траектории описываемые сходственными частицами жидкости обеих систем, геометрически подобны и одинаково ориентированы по отношению к границам этих систем;

б) скорости u и ускорения w в сходственных точках и в соответственные моменты времени всюду связанны постоянными соотношениями:

По всему объекту

В связи с кинематическим подобием возникает понятие масштаба времени:

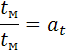
Где t_м , t_н – промежутки времени, в течении которых протекают соответственные явления вмодели и в натуре.

a_t=const

3. Динамическое подобие

Две гидравлические системы будут подобными в том случае если:

а) в любой паре сходственных точек действуют одноименные силы;

б) соотношение величин соответствующих сил для любой пары сходственных точек одинаково по всему объему обоих рассматриваемых гидравлических систем, т.е. масштаб сил:

в) силы, действующие на первую гидравлическую систему, ориентированы относительно друг друга и границ системы так, как и силы действующие на вторую гидравлическую систему.

Динамически подобными системами будут такие, для которых векторные поля сил, действующих на жидкость, образованны одноименными силами, причем эти поля являются геометрически подобными и одинаково ориентированными относительно границ систем. В связи с вопросом о динамическом подобии возникает понятие масштаба плотности жидкости:

Важно подчеркнуть, что для динамически подобных систем часто получаем:

а) для коэф-ов сопротивления ξ

ξ_м= ξ_н

б) для коэф-ов гидравлического трения λ

λ_м=λ_н

в) для коэф-ов Шези C

C_м=C_н

Судить о динамическом подобии двух систем путём измерения и сравнения м/д собой сил, действующих на эти системы практически неудобно и не возможно. Вместе с тем видно, что соотношение сил, действующих в натуре и на модели, может быть установлено косвенно: по имеющимся масштабам длины, скорости и плотности жидкости, т.е. по соотношению величин, легко поддающихся измерению.

Принимая такой косвенный метод оценки динамического подобия, пользуемся так называемыми критериями динамического подобия.