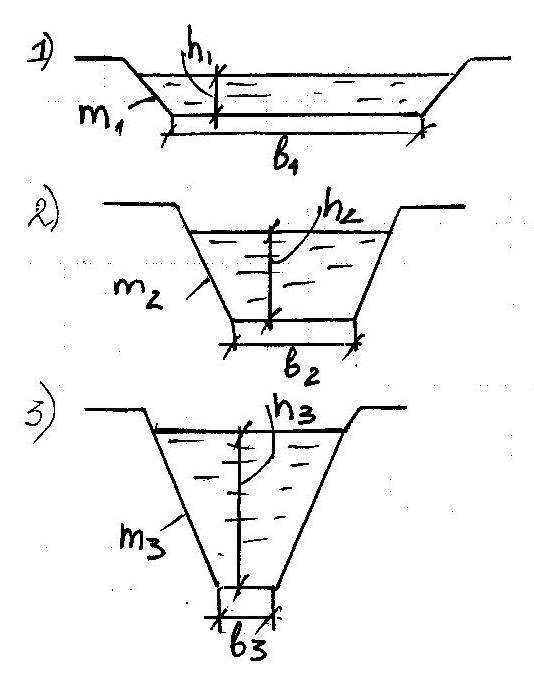
- •1.Установившееся движение жидкости в напорных трубопроводах
- •3. Понятие коротких и длинных трубопровод. Простой трубопровод постоянного диаметра.
- •4. Простой трубопровод. Случай истечений жидкости под уровень. Окончательные расчётные зависимости(?)
- •5.Особые случаи простоготрубопровода: сифон
- •7. Длинные трубопроводы. Истечение под уровень и в атмосферу.
- •12, Неустановившееся напорное движение жидкости. Гидравлический удар с учетом сжимаемости жидкости и упругими стенками трубопровода. Предварительные указания.
- •13 Расчетные зависимости для величины гидравлического удара и скорости его распространения.
- •14, Прямой (начальный) и отраженный гидравлические удары.
- •16. Истечение жидкости из малого отверстия в тонкой плоской стенке при постоянном напоре в атмосферу.
- •17.Типы сжатия струи. Коэффициенты φ, ξ ε,μ для малого отверстия при истечении в атмосферу, инверсия струи. Траектория струи.
- •18. Истечение из малого отверстия под уровень. Понятие малого и большого отверстий.
- •19.Типы насадков. Общая картина движения жидкости при истечении в атмосферу из насадка Вентури.
- •И стечение из внешнего круглоцилиндрического насадка в атмосферу. Расчетные зависимости для q и vb. Численные значения коэффициентов φ, ξ ε, μн.
- •21.Сопоставление истечения жидкости через отверстие в тонкой стенке с истечением через насадок Вентури. Величина вакуума. Работа короткой трубы.
- •22. Истечение в атмосферу или под постоянный уровень жидкости при переменном напоре.
- •23. Истечение газов из отверстий.
- •24. Относительное движение тела и жидкости. Общие сведения.
- •25. Сопротивление давления при обтекании жидкостью твердого тела.
- •27. Давление ветра на здание и сооружение.
- •28. Сопротивление трение. Пограничный слой.
- •30.Равномерное безнапорное установившееся движение воды в каналах.Предварительные замечания.
- •31.Гидравлические элементы живого сечения потока в канале.
- •32. Гидравлически наивыгоднейший поперечный профиль трапециидального канала.
- •33. Основные задачи при расчете трапециидальных каналов на равномерное движение воды.
- •34. Ограничение скорости движения воды при расчёте каналов.
- •35. Основные указания о моделировании гидравлических явлений.
- •36. Понятия о подобии гидравлических явлений.
- •37. Основы теории физического моделирования гидравлических явлений. Общие указания.
- •38. Критерии динамического подобия.
30.Равномерное безнапорное установившееся движение воды в каналах.Предварительные замечания.
Рассмотрим только турбулентное движение воды, относящееся к к квадратичной области сопротивления. На рисунке:
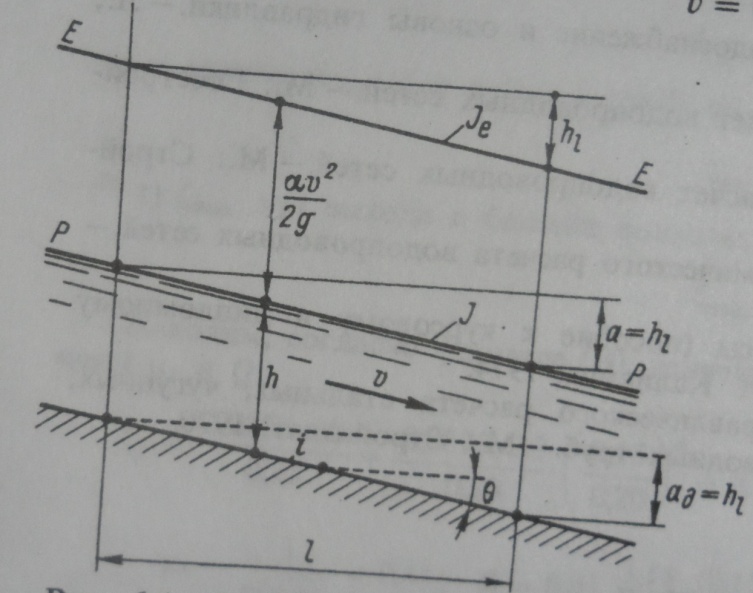
представлена схема
рассматриваемого движения, из которой
видно, что уклон дна канала i
= sin
![]() ,поскольку
величина L
измеряется вдоль наклонной линии дна
канала (угол
см. на
рисунке). Такое движение воды получается
в искусственных цилиндрических
каналах. В том случае, когда канал имеет,
в частности, земляное русло (что особенно
часто встречается в практике) скорости
v
в канале
назначаются сравнительно малыми (чтобы
не получить размыва грунта); при этом и
уклоны дна земляных каналов получаются
также небольшими. В связи с этим для
земляных (и некоторых других) каналов
можно считать, что i
= sin
,поскольку
величина L
измеряется вдоль наклонной линии дна
канала (угол
см. на
рисунке). Такое движение воды получается
в искусственных цилиндрических
каналах. В том случае, когда канал имеет,
в частности, земляное русло (что особенно
часто встречается в практике) скорости
v
в канале
назначаются сравнительно малыми (чтобы
не получить размыва грунта); при этом и
уклоны дна земляных каналов получаются
также небольшими. В связи с этим для
земляных (и некоторых других) каналов
можно считать, что i
= sin![]()
![]() tg
.Как
видно, здесь мы можем поступать следующим
образом: а) расстояние L-измерять
по горизонтали, б) живые же сечения
потока считать вертикальными, измеряя
глубины h-
по вертикали.
Очевидно, в этом случае рис (на котором
дно канала показано с большим уклоном)
следует рассматривать как чертеж,
выполненный в искаженном масштабе
(вертикальном масштабе — относительно
крупном, горизонтальном - относительно
мелком; именно поэтому уклон дна канала
на этом рисунке получился большим).
Основные зависимости, используемые при
расчете таких каналов
(когда Jе
= J
= i
= tg
),
следующие: Q=
tg
.Как
видно, здесь мы можем поступать следующим
образом: а) расстояние L-измерять
по горизонтали, б) живые же сечения
потока считать вертикальными, измеряя
глубины h-
по вертикали.
Очевидно, в этом случае рис (на котором
дно канала показано с большим уклоном)
следует рассматривать как чертеж,
выполненный в искаженном масштабе
(вертикальном масштабе — относительно
крупном, горизонтальном - относительно
мелком; именно поэтому уклон дна канала
на этом рисунке получился большим).
Основные зависимости, используемые при
расчете таких каналов
(когда Jе
= J
= i
= tg
),
следующие: Q=![]() = const
(вдоль потока);
= const
(вдоль потока);
![]()
последнюю
зависимость, учитывая, что в данном
случае ![]() и что J
= i
переписываем в виде
и что J
= i
переписываем в виде ![]() =
=![]() .
Также необходимо пользоваться такими
формулами как:
.
Также необходимо пользоваться такими
формулами как:
 ;
; ![]() ;
;
![]() ;
;
![]() .
.
![]() -расходная
характеристика
-расходная
характеристика
31.Гидравлические элементы живого сечения потока в канале.
Наиболее часто встречающиеся:
а)*симметричное трапецеидальное поперечное сечение.
Где-b-ширина канала по дну ;h-глубина наполнения канала;m-коэффициент откоса.
Ширина потока поверху:B=b+2mh.
Величины живого сечения w и смоченного периметра χ опреде-т по зависимостям:w=(b+mh)
Χ=b+2h![]()
В)*
Прямоугольное поперечное сечение.
Здесь B=mh;
w=m![]() ;
χ=2h
;
χ=2h
Б)*Треугольное поперечное сечение. b =0; B=2mh; w= m ; χ=2h
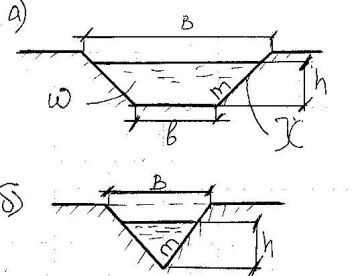
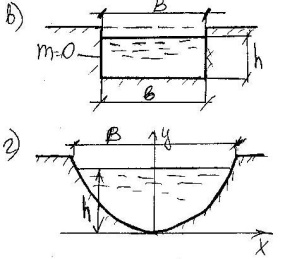
Г)*
Параболическое поперечное сечение.
Уравнение параболы, образующей смоченный
периметр: ![]() =2py,
где p-параметр
параболы. x
и y
–оси координат. W=
=2py,
где p-параметр
параболы. x
и y
–оси координат. W=![]() Bh
Bh
32. Гидравлически наивыгоднейший поперечный профиль трапециидального канала.
Предположим, что нам задана1) форма поперечного сечения канала.2) коэф. Откоса канала m 3) уклон дна канала i 4) коэф. Шероховатости n5) расход Q. Положим что исходя их этих данный требуется запроектировать поеречный профиль канала(.е.е найти его размеры). ТАКАЯ ЗАДАЧА ИМЕЕТ МНОГО ЕРШЕНИЙ. МОЖНО НАЙТИ ЦЕЛЫЙ РЯД различных поперечных профилей канала, удолетвор. указанным условиям.
В связи с анализов проведенных расчётов практически наивыгоднейшей величиной βг.н. при которой величина ω будет отличаться от ωmin менее чем на 3,4%, причём каналы будут получаться сравниттельном алой глубины, величина βг.н может лежат в пределах βг.н≤ βг.н0≤ (βг.н)пред. Где принимаемая величинаβ обозначена βг.н0. эту величину можно найти по формуле βг.н0=2,5+m/2
Β=(3-:-4)