1.Установившееся движение жидкости в напорных трубопроводах

Будем рассматривать установившееся, равномерное (параллельноструй-ное), напорное, турбулентное движение любой жидкости в круглых цилинд­рических неподвижных трубах. .Внутренний диаметр труб обозначаем через D, длину их через /. Гидра­влические элементы живого сечения рассматриваемого потока:

Главнейшие уравнения, которыми ниже будем пользоваться:

1. уравнение неразрывности — уравнение баланса расхода (3-38)—(3-40);

2. уравнение Бернулли — уравнение баланса удельной энергии (3-101);

3. уравнения для определения потерь напора (см. следующий параграф). Подчеркнем, что ниже будем иметь в виду исключительно случаи,

отвечающие квадратичной области сопротив­ления.

Что касается трубопроводов, относящихся к доквадратичной области сопротивления и области гладких русел (труб), то расчет их отли­чается от расчетов, приводимых ниже, только тем, что при определении потерь напора вместо формулы Шези здесь приходится пользоваться исклю­чительно формулой Вейсбаха—Дарси и находить коэффициент тре­ния X, как указано в

Расчетные зависимости для определения потерь напора

При расчете трубопроводов следует различать два случая. 1 случай когда местные потери напора отсутствуют, или когда этими потерями можно пренебречь—ввиду их малости сравнительно с поте­рями по длинеине (например,составляет величину, меньшую 5% от потерь напора hi).

В этом случае практически имеем только потери напора h_{, причем в ы -ражаем их через модуль расхода К согласно зависимо­сти :

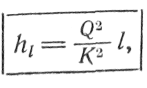^где

^{Что касается величины К2, то для круглой трубы}

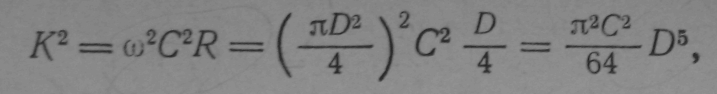(5-4)

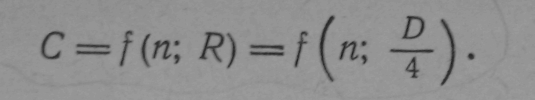I (5-5)

для квадратичной области сопротивления

I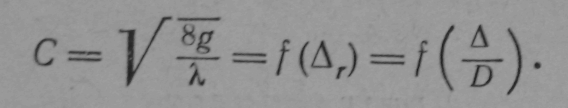 I (5-6)

Отсюда видно, что модуль расхода является функцией шероховатости

диаметра трубы. Если рассматривать, например, чугунные трубы,

имеющую определенную шероховатость, то можно сказать, что для них мо-

дуль расхода является функцией только диаметра трубы.имея это ввиду Для чугунных труб приводятся таблицы, в которых величины К (и К²) даются в зависимости от D. По этим

таблицам зная D, можно определить К (или К⁹); и, наоборот, зная К (или К² найти

2-й с л у ч а й, когда имеются местные потери напора J] h_]f причем ими нельзя пренебрегать сравнительно с величиной hi. Здесь величину h_t у д о б-нее.выражать через скоростной напор согласно зависи­мости Вейсбаха—Дарси:

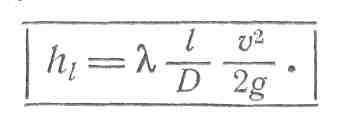
(5

3. Понятие коротких и длинных трубопровод. Простой трубопровод постоянного диаметра.

Простым трубопроводом называют трубопровод не имеющий боковых ответвлений.

Рассмотрим следующие случаи простых трубопроводов:

.случай истечения в атмосферу.

; ; ; - ?

;

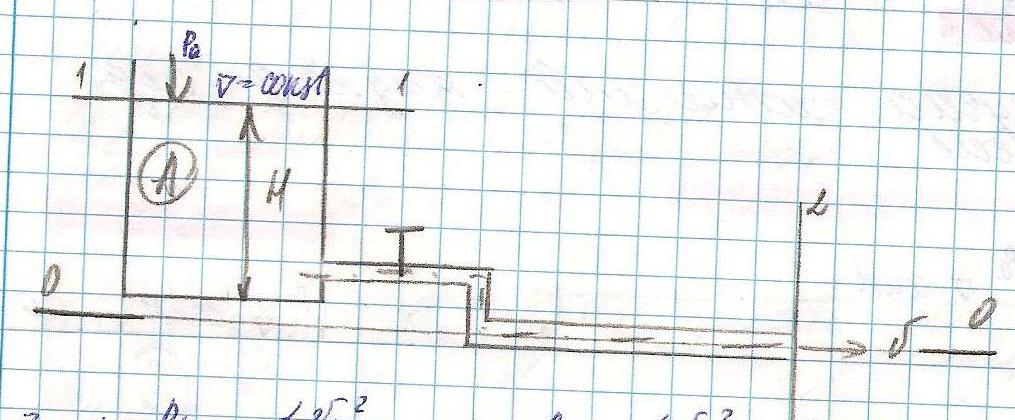
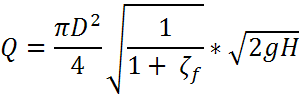
4. Простой трубопровод. Случай истечений жидкости под уровень. Окончательные расчётные зависимости(?)

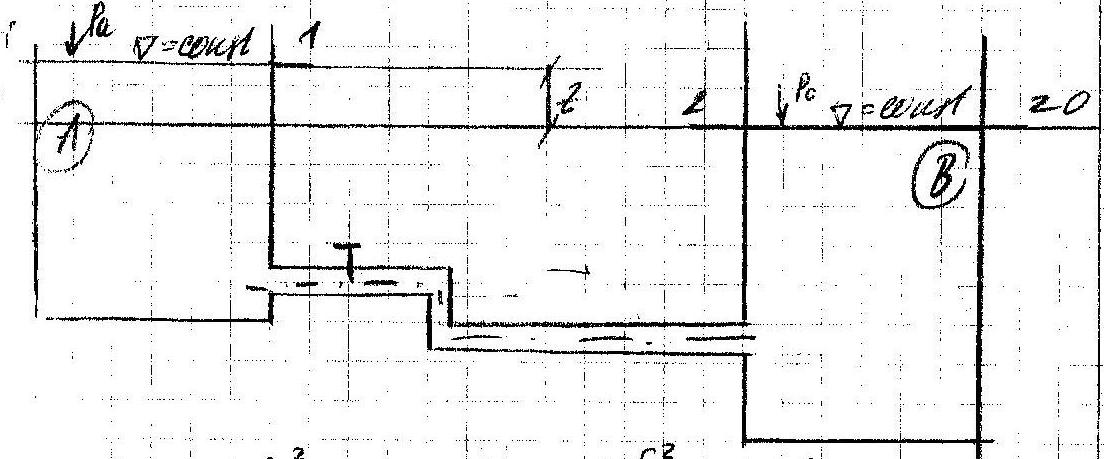
; = ; =0

; = ; =0; h-?

z=

z= =

;

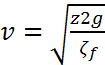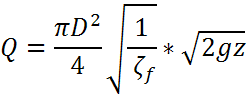
5.Особые случаи простоготрубопровода: сифон

Сифоном называется самотечная труба, часть которой расположена

Ограничимся рассмотрением истечения жидкости из сифона под уровень.

Если трубу, представленную на чертеже, каким-либо образом заполнить

ж идкостью, то после этого начнется движение жидкости из

верхнего сосуда

в нижний. В том, что жидкость в такой трубе будет двигаться, можно убедиться из следующего. Наметим сечение трубы п—п и обозначим превышение его над горизонтом жидкости: в левом сосуде — через и в правом со­суде — через I Если предпо­ложить, что жидкость, заполняющая сифон, находится в покое, то

" можем написать: а) давление в сечении n—п слевой стороны

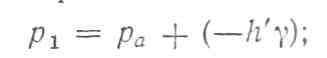
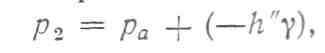
б) давление в сечении п—n с правой стороны

— соответствующие заглубления сечения под горизонтом

жидкости в сосудах (эти заглубления отрицательны);.

Характерным для сифона является то, что в нем имеет место вакуум. Наибольшая величина вакуума будет в сечении, наиболее высоко располо­женному т. е. в сечении п—п.

Найдем максимальную величину вакуума (h_вак)_максв в сифоне. С этой целью наметим по линии л—л, где ищем вакуум, сечение 2—2 и затем соеди­ним сечении /—/ и 2—2 уравнением Бернулли (плоскость сравнения про­ведем на уровне горизонта жидкости в левом сосуде):

Потери напора h_l на пути от сечения /—/ до сечения 2—2 выражаем обычной зависимостью:

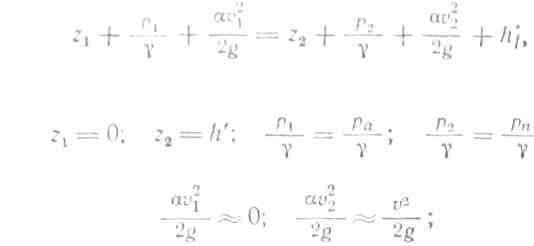
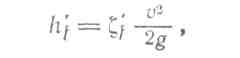
где £ — полный коэффициент сопротивления, учитывающий потерю напора не во всей трубе, а только от сечения /—1 до сечения 2—2. Подставляя получаем:

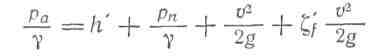
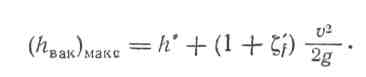
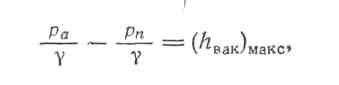
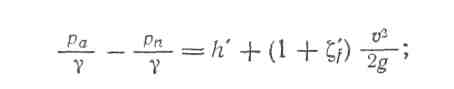
6 Всасывающая труба насоса. «Вса­сывающей трубой» насоса называется труба, по которой насос засасывает жид­кость из бассейна .Эта труба обычно так же, как и сифон, характеризуется наличием вакуума.

Наибольшая величина вакуума будет непосредственно у насоса, перед его рабочим колесом I (в сечении 2—2). Такой вакуум можно найти, соеди­няя уравнением Бернулли сечение /—/, намеченное по поверхности жидко­сти в бассейне, и сечение 2—2. Его можно также определить подставив в эту формулу вместо А' величину а, означающую превыше­ние оси насоса над горизонтом жидкости в бассейне, и вместо £/ величину t,_f, т. е. полный коэффициент сопротивления, учитывающий потери напора во всей трубе. При этом получаем:

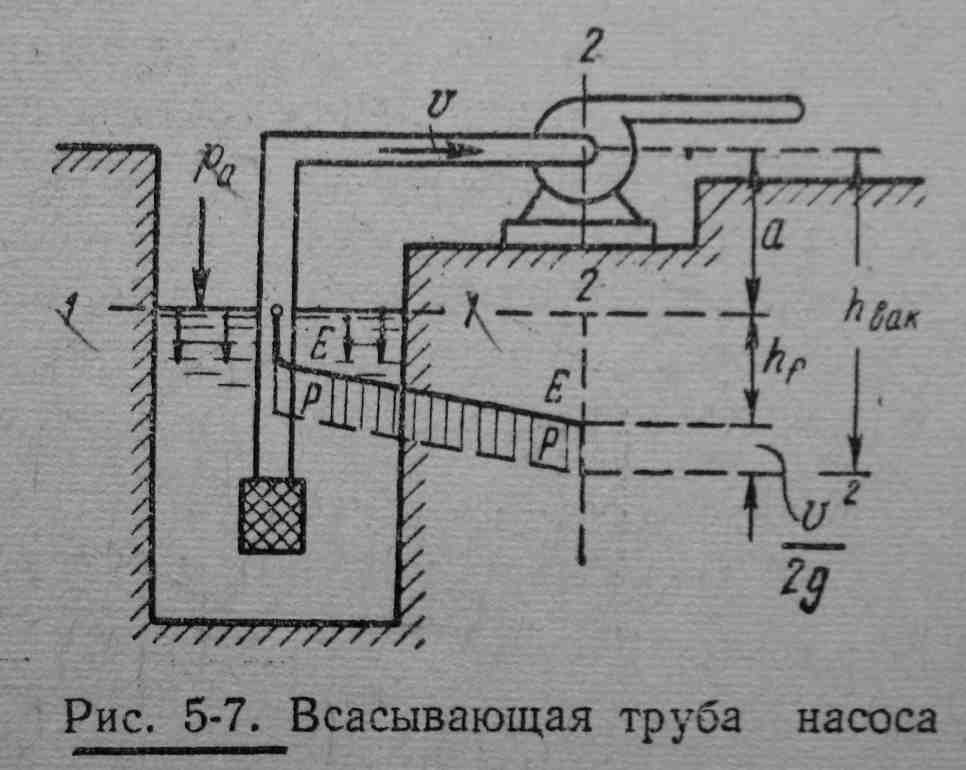
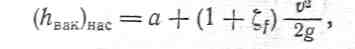
где, — вакуум перед рабочим колесом насоса.

Если оказывается большим, то при этом возникает кавитация

которая обусловливает снижение коэффициента полезного дей-J3bhh насоса, а также эрозию лопастей насоса.

Различные типы насосов допускают различную величину вакуума. Обычно вакуум перед рабочим колесом насоса должен удовлетворять условию:

Величина допустимого вакуума зависит не только от типа на­соса, но и от температуры и рода жидкости. С увеличением температуры жид­кости величина допустимого вакуума^снижаегсдЛПоскольку с повышением температуры кавитация усиливается;'см. § 1 -5). Например, при температуре воды, равной 60° С, допустимый вакуум приобретает уже отрицательное

значение (т. е. насос должен работать при давлении в воде, большем атмо­сферного).

Зная допустимый вакуум для данного насоса и данной жидкости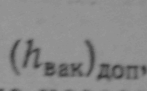 можно по формуле найти предельное максимальное возвышение над горизонтом жидкости в бассейне:

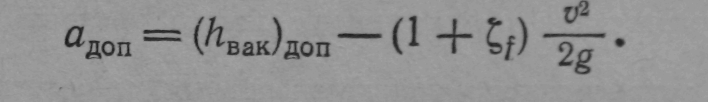
В случае горячей воды может быть отрицательным; в этом случае насос приходится располагать ниже горизонта воды в колодце.