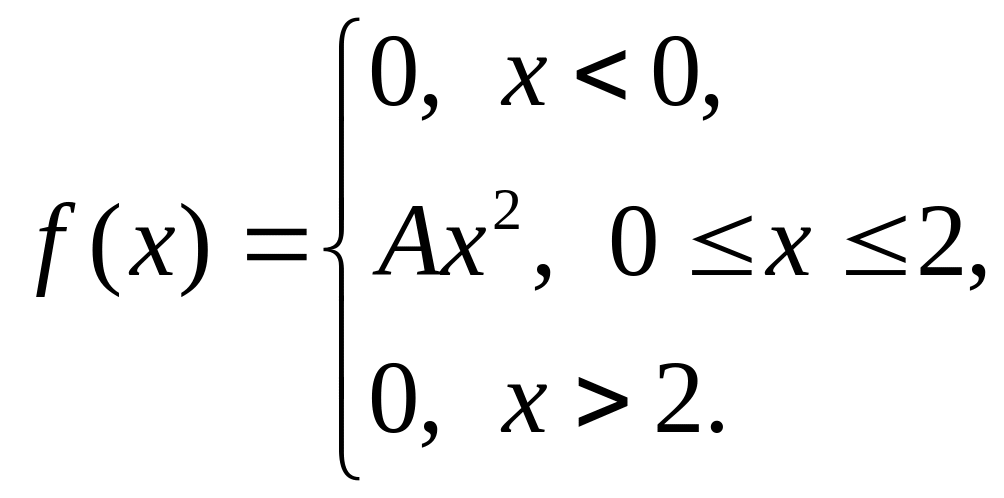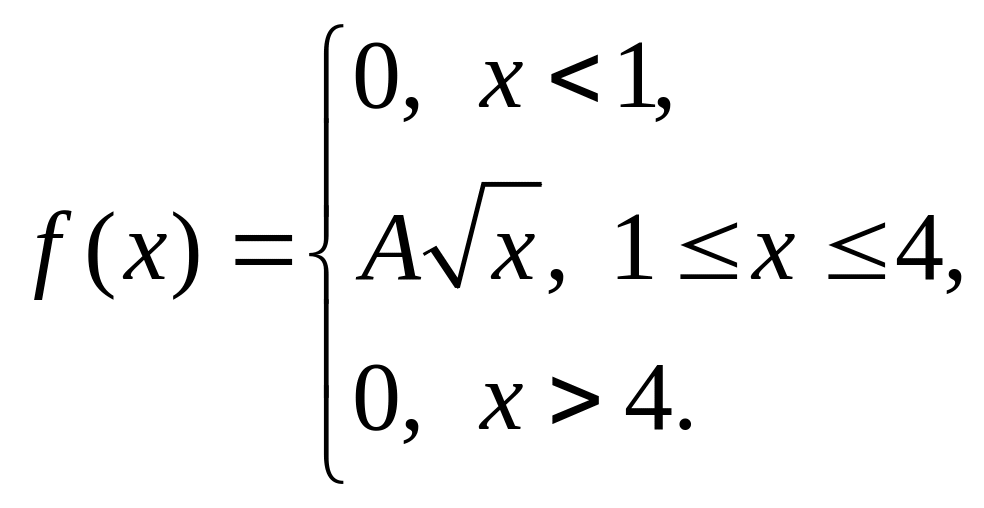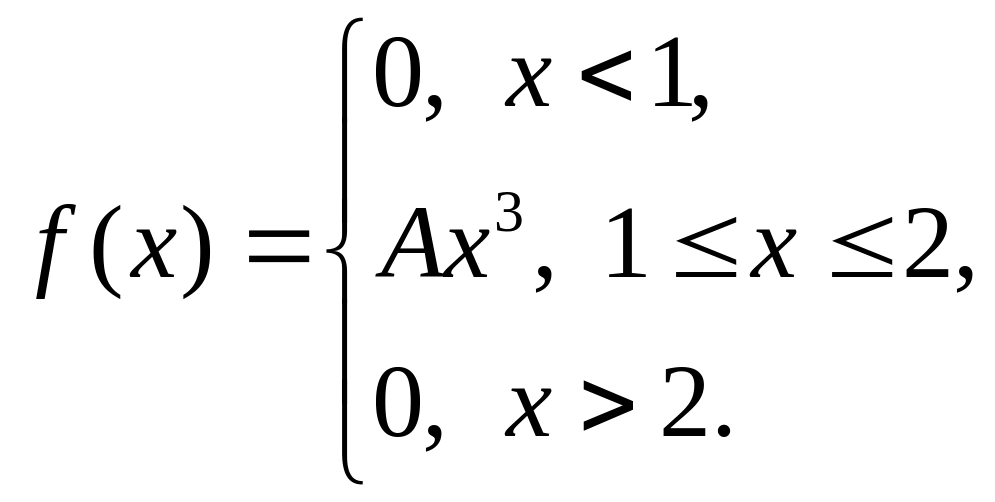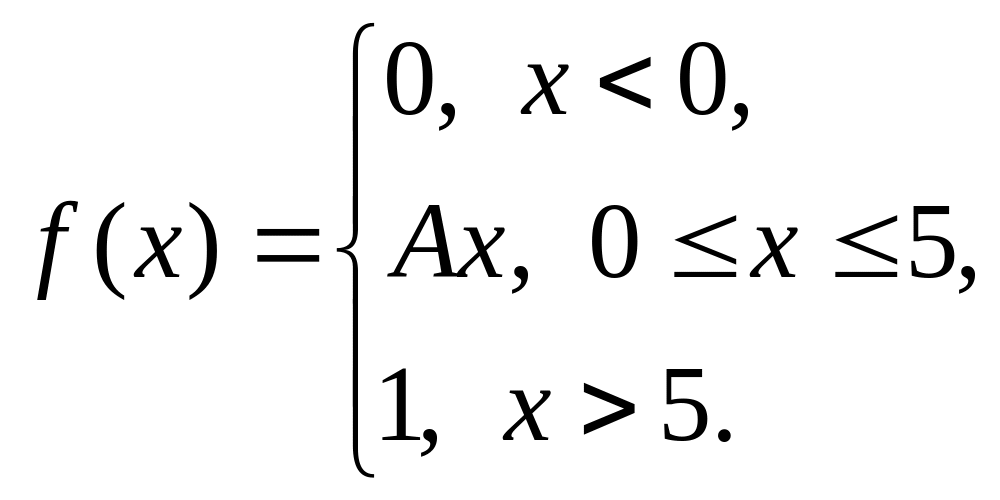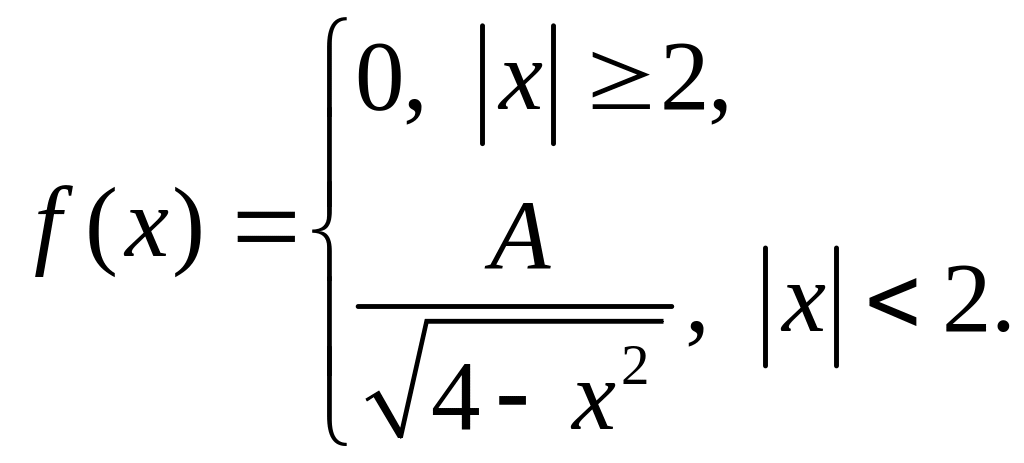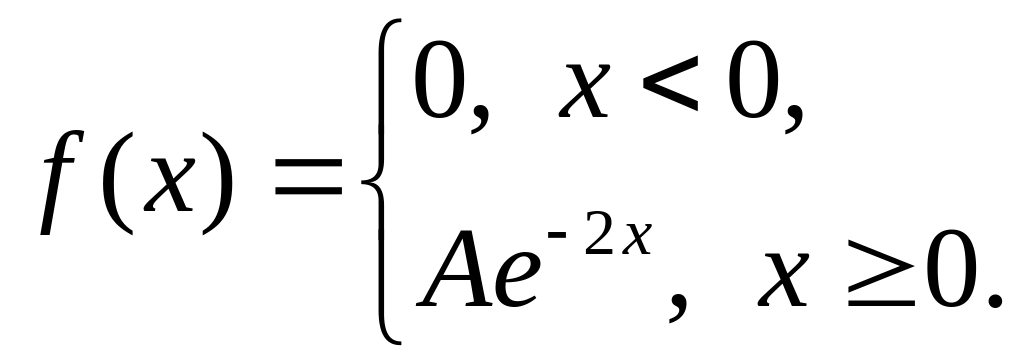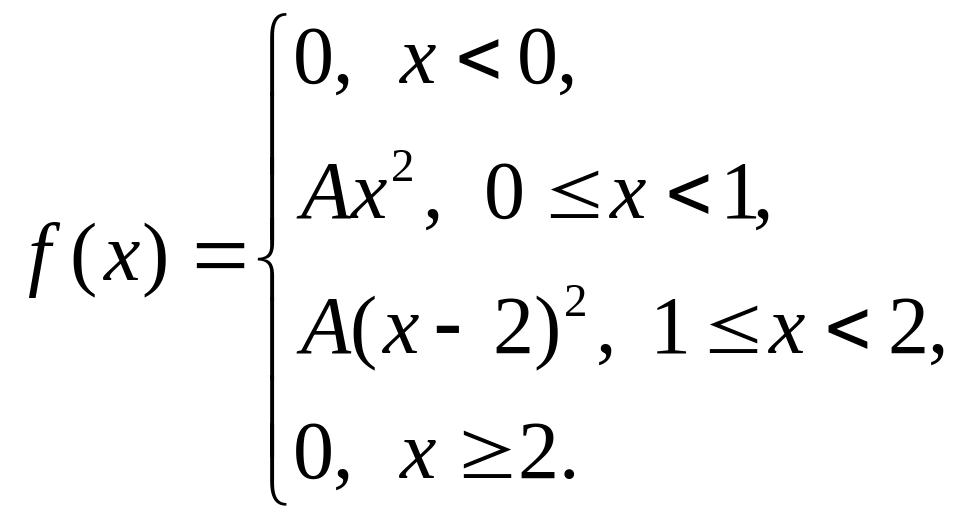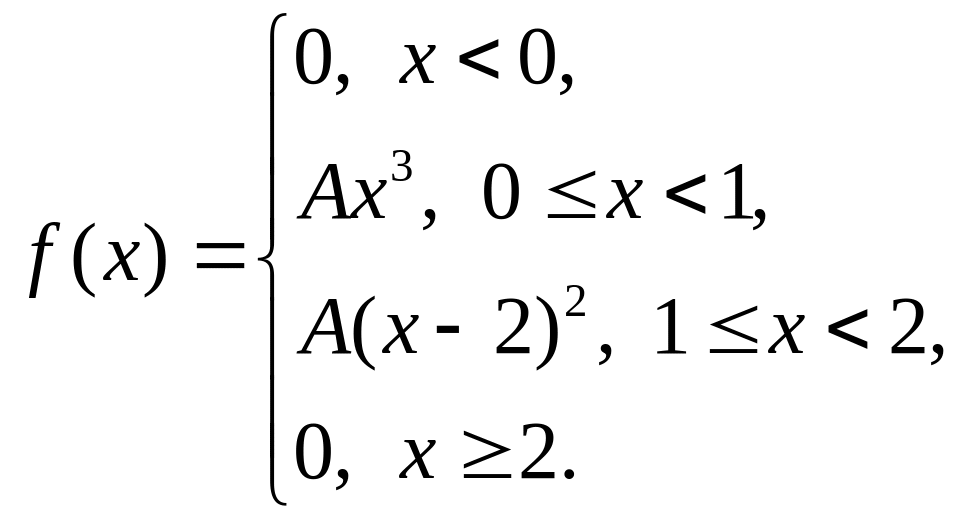Задача 2

Функции распределения и плотности распределения случайной величины.

191 – 196. Задана функция плотности распределения вероятностей f(x) непрерывной случайной величины Х.

191.		 = 1,  = 1,7.
192.		 = 2,  = 3.
193.		 = 1,1,  = 1,5.
194.		 = 3,  = 3,5.
195.		 = 2,  = 3.
196.		 = 0,5,  = 1.

Уровень I

Требуется:

1. Найти коэффициент А;

2. Найти функцию распределения F(x);

3. Схематично построить графики F(x), f(x).

Уровень II

Требуется:

1. Найти коэффициент А;

2. Найти функцию распределения F(x);

3. Схематично построить графики F(x), f(x);

4. Найти математическое ожидание и дисперсию Х;

5. Найти вероятность того, что Х примет значение из интервала (, ).

197 – 200. Задана функция распределения вероятностей F(x) непрерывной случайной величины Х.

197.		 = 1,  = 2.
198.		 = 2,  = 3.
199.		 = 1,  = 2.
200.		 = 2,  = 4.

Уровень I

Требуется:

1. Найти функцию плотности распределения вероятностей f(x);

2. Найти коэффициент А;

3. Схематично построить графики F(x), f(x).

Уровень II

Требуется:

1. Найти функцию плотности распределения вероятностей f(x);

2. Найти коэффициент А;

3. Схематично построить графики F(x), f(x);

4. Найти математическое ожидание и дисперсию Х;

5. Найти вероятность того, что Х примет значение из интервала (, ).

191 – 200. Уровень III

Задана функция плотности распределения вероятностей f(x) непрерывной случайной величины Х.

Требуется:

1. Найти коэффициент А;

2. Найти функцию распределения F(x);

3. Схематично построить графики F(x), f(x);

4. Найти математическое ожидание и дисперсию Х;

5. Найти вероятность того, что Х примет значение из интервала (, ).

191.		 = 0,  = 0,25.
192.		 = 0,  = 1.
193.		 = 0,  = 1.
194.		 = 0,  = 1.
195.		 = 0,  = 1.
196.		 = 0,  = 1.
197.		 = 0,  = 1.
198.		 = 0,  = 1.
199.		 = 0,  = 1.
200.		 = 0,  = 1.

Задача 3

Нормальное распределение.

201 – 210. Заданы математическое ожидание a и среднее квадратическое отклонение σ нормально распределенной случайной величины Х.

201.	a = 1, σ = 5, α = 0,5, β = 3.	202.	a = 9, σ = 5, α = 2, β = 8.
203.	a = 2, σ = 4, α = 1, β = 5.	204.	a = 8, σ = 3, α = 1, β = 6.
205.	a = 3, σ = 2, α = 2, β = 8.	206.	a = 6, σ = 4, α = 0, β = 5.
207.	a = 4, σ = 4, α = 3, β = 6.	208.	a = 4, σ = 6, α = 5, β = 9.
209.	a = 5, σ = 6, α = 4, β = 9.	210.	a = 2, σ = 3, α = 4, β = 8.

Уровень I

Найти вероятность того, что Х примет значение из интервала (, ).

Уровень II

Требуется:

1. Написать функцию плотности распределения вероятностей f(x) и схематично построить ее график;

2. Найти вероятность того, что Х примет значение из интервала (, ).

Уровень III

201. Случайная величина Х имеет нормальное распределение с параметрами a = 10, σ = 2. Найти ее функцию распределения вероятностей F(x).

202. Случайная величина Х имеет нормальное распределение с параметрами a, σ. Вычислить вероятность Р_к того, что отклонение величины Х от ее математического ожидания не превзойдет величины кσ (ответ получить для трех значений к = 1,2,3).

203. Случайная величина Х имеет нормальное распределение с параметрами a = 10, σ = 2. Найти симметричный относительно а интервал, в котором с заданной вероятностью Р попадает измеряемое значение Х. Рассмотреть следующие числовые значения: 1) Р₁ = 0,9974; 2) Р₂ = 0,9544; Р₃ = 0,50.

204. Отклонение длины изготовляемой автоматом детали от стандарта является случайной величиной, распределенной по нормальному закону. Какую точность длины детали можно гарантировать с вероятностью 0,8, если стандартная длина детали равна 50 см, а среднее квадратическое отклонение равно 0,1 см?

205. Случайная величина Х имеет нормальное распределение с параметрами a, σ. Найти вероятность попадания Х в интервал (a + σ, a + 3σ).

206. Случайная величина Х имеет нормальное распределение с математическим ожиданием a = 20. Вероятность попадания Х в интервал (15, 20) равна 0,4. Найти вероятность попадания Х в интервал (20, 25).

207. Случайная величина Х имеет нормальное распределение с математическим ожиданием a = 25. Вероятность попадания Х в интервал (10, 15) равна 0,3. Найти вероятность попадания Х в интервал (35, 40).

208. Случайная величина Х имеет нормальное распределение с математическим ожиданием a = 10. Вероятность попадания Х в интервал (8, 12) равна 0,4. Найти значение среднего квадратичного отклонения σ величины Х.

209. Случайная величина Х имеет нормальное распределение с математическим ожиданием a = 1,6 и средним квадратическим отклонением σ = 1. Найти вероятность того, что при четырех испытаниях Х попадет хотя бы один раз в интервал (1, 2).

210. Случайная величина Х имеет нормальное распределение с математическим ожиданием a = 2 и средним квадратическим отклонением σ = 0,5. Найти вероятность того, что при первом испытании Х окажется на отрезке [3, 4], а при втором – на отрезке [1, 2].