2. Квантовая гипотеза. Формула Планка.
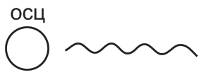излучение
непрерывно.
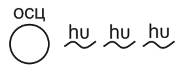W=hυN
r υT = 2Piυ2 <ε> /C2
r λT = 2PiC<ε> /λ4
<ε> = hυ / (e hυ/kT - 1)
<ε> = hC / λ (C hC/kTλ - 1)
r υT = (2Piυ2 /C2 )*( hυ / (e hυ/kT - 1))
r λT = (2PiC /λ5)*( hC / e hC/kT - 1)
3. Следствие из формул Планка.
Первое: υ – мало; hυ<<kT
e hυ/kT – мала
e hυ/kT = 1 + hυ/kT + (hυ/kT)2 /2! + . . .
e hυ/kT ~ 1 + hυ/kT
r υT = (2Piυ2 /C2 )*( hυ / (1 + (hυ/kT) - 1) = 2Piυ2kT/C2
Второе: υ – большие; hυ>>kT
e hυ/kT – большие
e hυ/kT>>1
r υT = (2Piυ2 /C2 )*( hυ e -hυ/kT)
Третье:
Re=(интеграл от 0 до бесконечности)( (2Pih /C2 )*( υ3 / (e hυ/kT - 1)*dυ))= (2Pih /C2 ) (интеграл от 0 до бесконечности)( ( υ3 / (e hυ/kT - 1))*dυ)
hυ/kT = x υ = kTx/h
dυ = kTdx/h
Re=(2Pih /C2 ) (интеграл от 0 до бесконечности)((k3T3kTdx)/h3h(ex-1))
Re=(2Pik4T4/h3C2) (интеграл от 0 до бесконечности)(x3dx/ex-1)=2Pi5k4T4/C2h315
Re= σT4- (экспериментально)
Re = (2Pi5k4/C2h315)* T4 => (2Pi5k4/C2h315) = σ
σ = 5,67 * 10-8
h=(корень 3 степени)( 2Pi5k4/C2 σ 15)
d r λT/∂λ = 2PihC2 [(5/ λ6) / ( (e hυ/kT - 1) + (1/ λ5) ((hC/kT λ2 * e hC/kT λ)/( e hC/kT λ - 1) ) )]
d r λT/∂λ = [2PihC2/( λ6 ( e hC/kT λ - 1))] * (-5 + (hC/kT λ * e hC/kT λ)/( e hC/kT λ - 1))
hC/kT λ = x
d r λT/∂λ = [2PihC2/( λ6 ( e hC/kT λ - 1))] (xex – 5ex+5)
При λ = λ m, hC/kT λm = x
xex – 5ex+5=0
x=4,965= hC/kT λm
bλm=hC/4,965
Формула Планка удовлетворяет законам Стефана-Больцмана и Вина
§6 Оптическая пирометрия
Учебник параграф 201
Атомная физика
Глава 1. Ядерная модель атома.
§1 Закономерности линейчатых спектров.
Линии в спектре группируются в серии. Спектральная серия – совокупность спектральных линий убывающей интенсивности, сходящейся к определенному пределу.
Серия
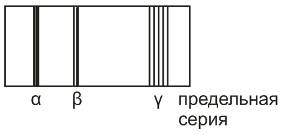
Бальмер
1/λ = R(1/22-1/n2) n=3,4,5… - спектр водорода
R=1,1* 10-7 м-1 (постоянная Ридберга)
1. Обобщенная (сериальная) формула Бальмира.
1/λ = R(1/ni2-1/nj2)
ni =1,2,3…
nj = (ni +1), (ni +2) …
1/λ=υ= CR(1/ni2-1/nj2)
RC=R’=3,29*1015 1/c
1.серия Лаймана (ультрафиолет)
ni =1 nj =2,3,4
υ= R’(1/12-1/nj2)
предел серии υпред = R’
2.серия Бальмира (видимый свет)
ni =2 nj =3,4,5
υ= R’(1/22-1/nj2)
3.серия Пашена (инфракрасная область)
ni =3 nj =4,5,6
υ= R’(1/32-1/nj2)
4.серия Брэкета (дол. Инфракрасной области)
ni =4 nj =5,6,7
υ= R’(1/42-1/nj2)
2. Строение атома.
1.Электрон (термо эл. Эмиссия, холодная эмиссия эл. Из металла, фотоэффект)
2.+ заряд
§2 Модель Томпсона.
Модель атома – сфера заряженного вещества, т.н. «Кекс с изюмом»
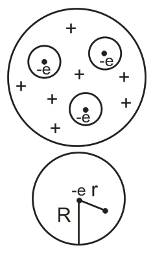
Атом водорода. Заряд сферы +e
Если электрон отклонить, то он притягивается назад с F=eE
E=ρr/3ε0
ρ=e/(4/3)PiR3
E=er/3 ε0 (4/3)PiR3 = er/4Piε0R3 (по т. Гаусса)
F=e2r/4Piε0R3 - квазиупругая сила
F=kr k – коэффициент упругости
Электрон в атоме ведет себя как грузик на пружинке.
(?) Частота колебаний электрона ω=sqr(k/m)
= частоте излучений электрона (?) ω=sqr(e2/4Piε0R3m ) ~ 10 15 1/c R ~ 3 10 -10 м
[ω] = sqr (кл2 м / Ф м3 кг) = sqr (В Кл м / м3 кг) = sqr (Дж м / м3 кг) = sqr (кг м2 м / м3 кг с2) = 1/c
Частота видимого света (400 – 760 нм) в модели совпадает с полученной экспериментально частотой, однако эта теория просуществовала всего с 1903 – 1911