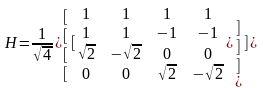- •1. Определение цос. Основные задачи. Примеры использования. Структурная схема цос. Режимы работы устройств цос.
- •2. Типовые сигналы цос. Нормирование времени и частоты.
- •3. Определение z-преобразования. Область сходимости. Соотношение между z и p-плоскостями.
- •4. Основные свойства z-преобразований. Способы вычисления прямого и обратного z-преобразований.
- •5. Определение дискретной системы. Виды дискретных систем.
- •6.Импульсная и переходная характеристики. Формула свертки.
- •7.Разностные уравнения. Бих и ких-системы. Свойство памяти линейных дискретных систем (лдс).
- •8.Передаточная функция. Карта нулей и полюсов . Критерий устойчивости лдс.
- •9.Структурные схемы лдс. Прямая, каскадная и параллельная структуры.
- •10.Канонические структуры лдс.
- •11. Дискретное преобразование Фурье (дпф).
- •12. Свойства дпф. Теорема Парсеваля.
- •13. Алгоритм вычисления свертки с помощью дпф.
- •14. Унитарные преобразования. Косинусные преобразования.
- •15. Унитарные преобразования. Преобразование Адамара.
- •16.Преобразование Хаара. Вейвлет-преобразование. Преобразование Хаара
- •17.Архитектура и классификация спецпроцессоров цос
- •18.Концепции архитектуры спецпроцессоров цос
- •19. Организация параллелизма в спецпроцессорах цос
- •20. Основные понятия цифровой обработки изображений.
- •21. Субъективные характеристики цвета.
- •22. Логарифмическая модель одноцветного зрения. Основные зрительные явления.
- •23. Модель цветного зрения.
- •24.Определение колориметрии. Основные способы уравнивания цветов.
- •25.Аксиомы уравнивания цветов Грассмана.
- •26. Цветовое пространство.Координаты цвета и координаты цветности.
- •27.Представление цифрового изображения
- •Смежность и связность пикселей на цифровом изображении. Меры расстояний.
- •Методы улучшения изображений. Основные градационные преобразования.
- •Методы улучшения изображений. Кусочно-линейные градационные преобразования.
- •Основы пространственной фильтрации.
- •32. Сглаживающие пространственные фильтры. Фильтры, основанные на порядковых статистиках.
- •Пространственные фильтры повышения резкости. Операторы Робертса, Собеля.
- •Алгоритм и структурная схема фильтрации в частотной области.
- •Сглаживающие частотные фильтры.
- •36. Частотные фильтры повышения резкости
- •37. Пространственные фильтры подавления шума.
- •Усредняющие фильтры
- •2. Фильтры порядковых статистиках
- •38. Адаптивные фильтры подавления шума.
- •39. Частотные фильтры.
- •40. Оценки искажающей функции.
- •41. Инверсная и Винеровская фильтрация.
- •42. Геометрические преобразования.
- •43. Сжатие изображений. Основные виды избыточности.
- •44. Кодовая избыточность.
- •45.Межэлементная(1) и визуальная (2) избыточности.
- •46.Основные алгоритмы сжатия без потерь.
- •47.Основные алгоритмы сжатия с потерями.
14. Унитарные преобразования. Косинусные преобразования.
Унитарные
преобразования являются частным случаем
линейных преобразований когда линейный
оператор точно обратим, а его ядро
удовлетворяет условиям ортогональности.

Дискретное косинусное преобразование — одно из преобразований. Вариант косинусного преобразования для вектора действительных чисел. Применяется в алгоритмах сжатия информации с потерями, например, MPEG и JPEG. Это преобразование тесно связано с Дискретным преобразованием Фурье и является гомоморфизмом его векторного пространства.
Математически преобразование можно осуществить умножением вектора на матрицу преобразования. При этом матрица обратного преобразования с точностью до множителя равна транспонированной матрице. Матрицы выбирают так, чтобы преобразование было ортонормированным, а постоянный множитель равен единице. В компьютерных приложениях это не всегда так.
Различные периодические продолжения сигнала ведут к различным типам ДКП. Ниже приводятся матрицы для первых четырех типов ДКП:
![]()
![]()
![]()
![]()
ДКП для вектора из 8 чисел часто называют ДКП -28. Наиболее распространён двумерный вариант преобразования для матриц 8x8, состоящий из последовательности ДКП -28 сначала для каждой строки, а затем для каждого столбца матрицы.
Существуют алгоритмы быстрого ДКП -преобразования, похожие на алгоритм быстрого преобразования Фурье. Для ДКП -28 и других вариантов ДКП с фиксированной размерностью вектора существуют также алгоритмы, позволяющие свести количество операций умножения к минимуму.
Существуют аналоги ДКП, приближающие косинус числами, легко получающимися путём небольшого количества операций сдвига и сложения, что позволяет избежать операций умножения и тем самым повысить эффективность вычислений. Преимущество таких аналогов — более высокая скорость.
Дискретное косинусное преобразование (ДКП)


15. Унитарные преобразования. Преобразование Адамара.
У![]() нитарные
преобразования являются частным случаем
линейных преобразований когда линейный
оператор точно обратим, а его ядро
удовлетворяет условиям ортогональности.
\
Самым
простым унитарным преобразованием
является преобразование Адамара.
Матрица
нитарные
преобразования являются частным случаем
линейных преобразований когда линейный
оператор точно обратим, а его ядро
удовлетворяет условиям ортогональности.
\
Самым
простым унитарным преобразованием
является преобразование Адамара.
Матрица ![]() для
случая двух случайных величин будет
иметь вид:
для
случая двух случайных величин будет
иметь вид:
В квадратной матрице Адамара все элементы равны либо +1, либо -1, а строки столбцы это ортогональные векторы

Легче ее строить если NxN = степени 2 (самая простая – H2)
Матрицу Адамара размерности 4х4 элементов легко построить из матрицы Адамара размерностью 2х2 элемента:
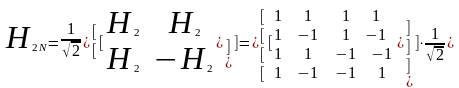
Пользуясь
данным соотношением можно построить
матрицу Адамара любой размерности ![]() ,
где
,
где ![]() -
любое целое положительное число. Анализ
изображений выполняется на основе
разделимого преобразования:
-
любое целое положительное число. Анализ
изображений выполняется на основе
разделимого преобразования:
![]() .
.
Так
как матрица
представляет
собой оператор ортогонального
преобразования, то обратное преобразование
из ![]() в
в ![]() запишется
в виде
запишется
в виде![]()
Для каждой строки матрицы можно приписать свойство секвента строки (изменение знака строки).



 , где
i
– номер разряда
, где
i
– номер разряда
Примечание: если U=1310=11012 , то U0 = 1, U1 = 0, U2 = 1, U3 = 1
Пример ядра преобразования Хаара