11. Дискретное преобразование Фурье (дпф).

Дискретное преобразование — это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов, а также в других областях, связанных с анализом частот в дискретном сигнале. Дискретное преобразование Фурье требует в качестве входа дискретную функцию. Такие функции часто создаются путём дискретизации(выборки значений из непрерывных функций). Дискретные преобразования Фурье помогают решать частные дифференциальные уравнения и выполнять такие операции, как свёртки. Дискретные преобразования Фурье также активно используются в статистике, при анализе временных рядов. Существуют многомерные дискретные преобразования Фурье.

Дискретным преобразованием Фурье периодической последовательности называется пара взаимно-однозначных дискретных рядов Фурье для последовательности во временной и частотной областях.

Прямое преобразование:

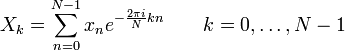
Обратное преобразование:

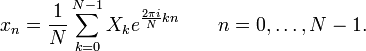
N — количество значений сигнала, Xn - измеренные значения сигнала которые являются входными данными для прямого преобразования и выходными для обратного;, Xk - являются выходными данными для прямого преобразования и входными для обратного;

– средняя яркость изображения

В этом случае:

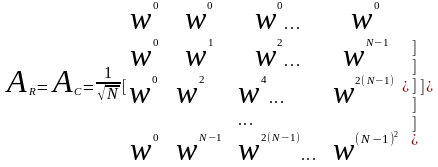, где

_Здесь Для ДПФ

12. Свойства дпф. Теорема Парсеваля.

Дискретным преобразованием Фурье периодической последовательности называется пара взаимно-однозначных дискретных рядов Фурье для последовательности во временной и частотной областях.

1). Если функция F(x,y) разделима, т. е. Её можно записать как F(x,y)=f(x)-f(y), то разделима и Фурье F_F(ω_x,ω_y)= f_F(ω_x) * f_F(ω_y)

2). Если функция F(x,y) симметрична, т. е. F(-x,-y) = ± F(x,y), то симметрична и фурье область F_F(-ω_x,-ω_y)= ±f_F(ω_x,ω_y)

3). Линейность – точечная последовательность равна линейности комбинации точечных последовательностей.:

Ơ_F{aF₁(x,y)+ bF₂(x,y)} =a F_F1(ω_x,ω_y)+ b F_F2(ω_x,ω_y)

4). Маштабирование

Ơ_F{F(ax,by)}=1/|ab| * F_F(ω_x/a,ω_y/b)

5). Сдвиг изображения. – умножение точечной последовательности на поворачивающий множитель приводит к сдвигу точечной ДПФ по оси k вправо на величину k0. . Аналогично, умножение последовательности приводит к сдвигу ДПФ по оси k влево на величину k0. .

Теорема Парсенваля. Под теоремой Парсеваля обычно понимают унитарность преобразования Фурье. То есть сумма (или интеграл) квадрата функции равна сумме квадрата результата преобразования.

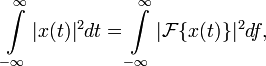
Где обозначает непрерывное преобразование Фурье, которое связывает временной или пространственный сигнал x(t) с его представлением в частотной области X(f).

В дискретном виде теорему записывают следующим образом:

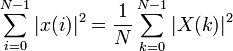
где X(k) представляет собой дискретное преобразование Фурье сигнала x(k), имеющего N отсчетов.

13. Алгоритм вычисления свертки с помощью дпф.

Линейное уравнение называются формулой свертки (сверткой): реакция у(nT) вычисляется как дискретная свертка воздействия x(nT) и импульсной характеристики h(nT).

ДПФ преобразует свертку последовательностей в произведение их образов. Это позволяет вычислить циклическую свертку y1 двух последовательностей hn и xm, используя ДПФ, по схеме: у1= , где y1= , l=0,…,N-1.

Поскольку ДПФ можно вычислять с помощью БПФ-алгоритмов, то этот метод требует, чтобы число операций было пропорционально NlogN и следовательно, меньше числа операций при прямом вычислении. Более точно, если используется БПФ-алгоритм по основанию 2 с одним фиксированным входом, то циклическая свертка последовательности длиной N= требует два БПФ и N комплексных умножений. Следовательно, число комплексных умножений будет M=N(1+ . Для больших N это значительно меньше, чем умножений, требуемых при прямом вычислении свертки.

Приминение ДПФ при вычислении круговой свертки:

Алгоритм расчета:

1. Определяется n-точечные ДПФ;

2) Вычисляется их произведение (поэлементное);

3) С помощью ОДПФ (обратного ДПФ) определяется n-точечная последовательность y(n).

Линейная свертка. Применяется в случае непериодических последовательностей.

Алгоритм:

1) Последовательности x1(n), x2(n) дополняются нулями до длины L=N1+N2-1. Тогда линейная свертка последовательностей будет равна L-точечной круговой свертке последовательностей;

2) Остальные шаги аналогичны круговой свертке.