9.Структурные схемы лдс. Прямая, каскадная и параллельная структуры.

Структурная схема — это совокупность элементарных звеньев объекта и связей между ними, один из видов графической модели. Под элементарным звеном понимают часть объекта, системы управления и т. д., которая реализует элементарную функцию.

Структурные схемы ЛДС отображают алгоритм вычисления реакции.

Способы построения:

1) на основании свертки; 2) с помощью передаточной функции.

В структурных схемах основные операции отображаются следующими элементами:

1) сумматор; Пример:

2) умножитель; Пример: 3)элемент задержки; Пример:

Z^-1

x(n) b b*x(n) x(n) x(n-1)

Структуры рекурсивных ЛДС:

Прямая структура-определяется передаточной функцией, представленной в дробно-рациональном виде: W(p)=(b₀+b₁z^-1+b₂z^-1)/( 1+a₁z^-1+a₂z^-1); и отображает разностное уравнение :

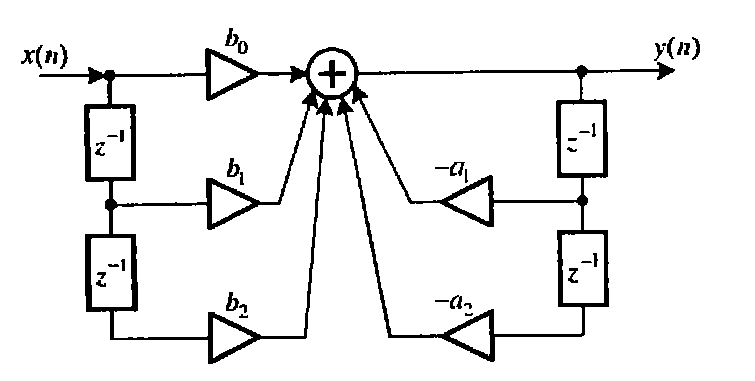
Структуру называют канонической, если число элементов задержки в ней минимально и равно порядку передаточной функции.

Каскадная структура-определяется передаточной функцией, представленной в виде произведения множителей второго порядка.

Параллельная структура-определяется передаточной функцией в виде суммы элементарных дробей второго порядка.

И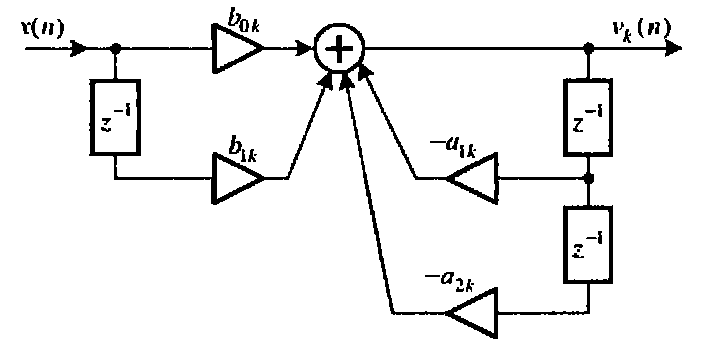 зобразим параллельную структуру состоящую из 3 звеньев 2-го порядка прямой и канонической структуры:

С труктуры нерекурсивных ЛДС

Прямая структура. Она определяется передаточной функцией H(z):

и отображает разностное уравнение:

Графически изображается так:

Каскадная структура. Она определяется передаточной функцией H(z) представленной в виде произведения множителей второго порядка.

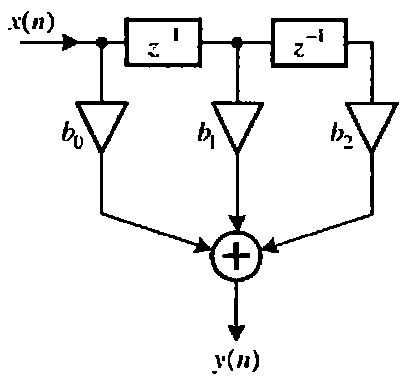
Изображается так:

10.Канонические структуры лдс.

Структуру называют канонической, если число элементов задержки в ней минимально и равно порядку передаточной функции.

Существует три канонические структуры.

1) Прямая каноническая структура 1:Определяется эквивалентным представлением функции H(z) в виде произведения двух передаточных функций:

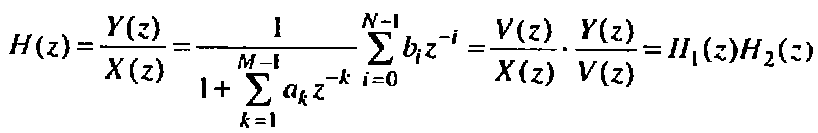
Одна из которых описывает рекурсивную часть:

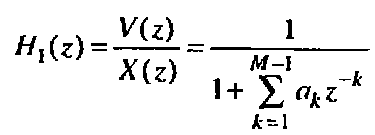
А вторая не рекурсивную:

Н₁(z) и H₂(z) соответсвуют следующие разностные уравнения:

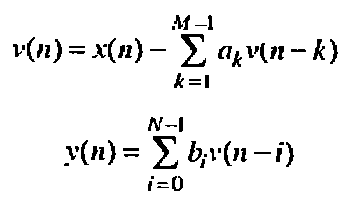
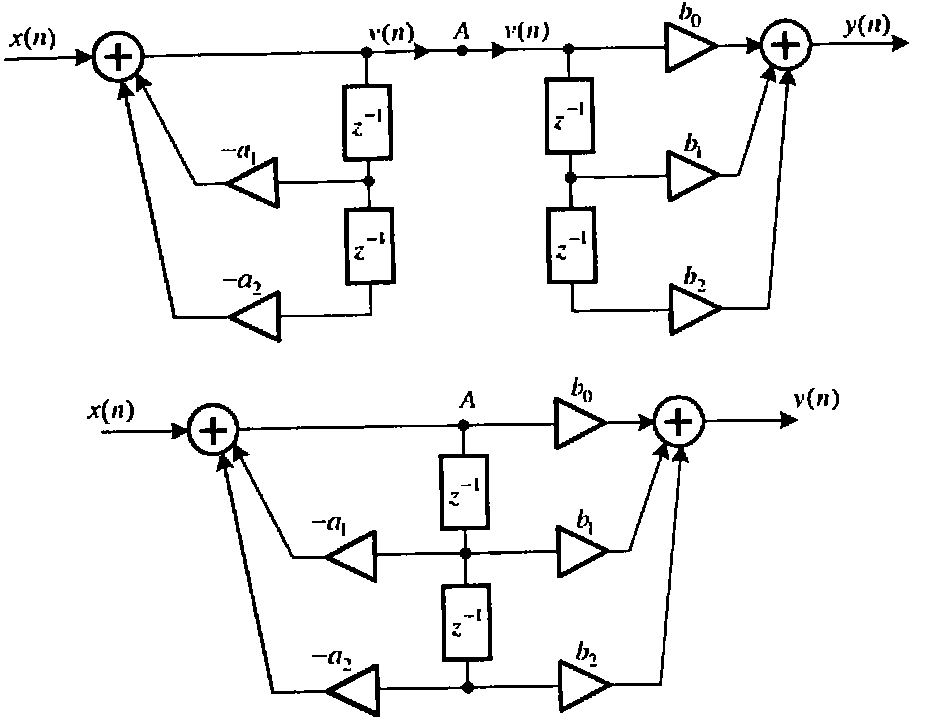
2)Каноническая структура 2:Определяется представлением передаточной функции H(z) которая получается путём деления числителя на знаменатель по правилу многочленов.

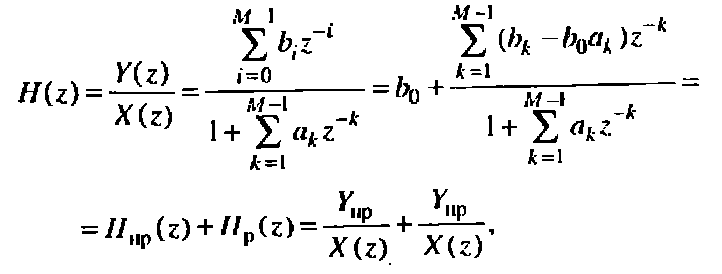
После чего H(z) представляется в виде суммы двух передаточных функций

Нерекурсивной(Н_нр):

И рекурсивной*(Н_р):

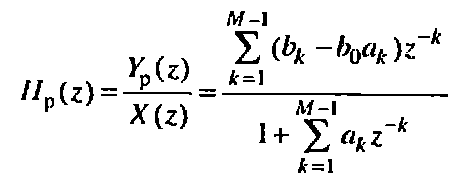
После преобразований получим для H(z) разностное уравнение:

Приведём пример канонической структуры 2-го звена 2-го порядка:

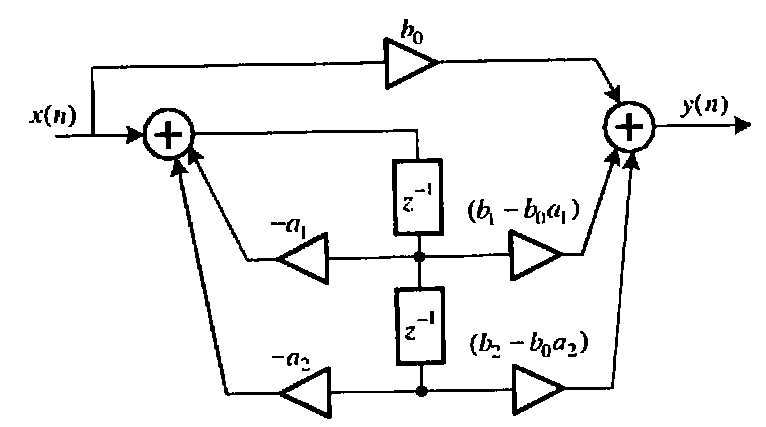
3)Каноническая структура 3: Определяется представлением функции H(z) которая получается следующим образом:

1)если N=Mи умножим левую и правую части на

Получим:

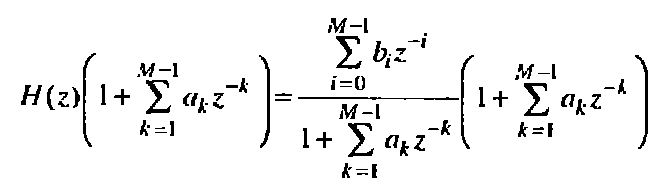
Проведя преобразования получим следующую систему:

Система решается снизу вверх и отображается канонической структурой 3 звена 2-го порядка: