7.Разностные уравнения. Бих и ких-системы. Свойство памяти линейных дискретных систем (лдс).

Взаимосвязь между воздействием x(nT) и реакцией y(nT)-это является соотношение вход/выход – может быть описано разностным уравнением:

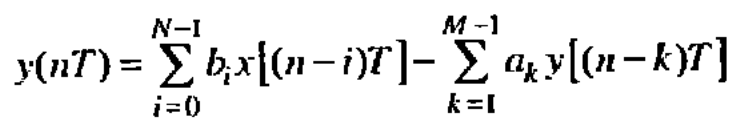
Если такая система описана разностным уравнением то она отвечает условиям физической реализуемости: т.е. при нулевых начальных условиях реакция не может возникнуть раньше воздействия.

БИХ и КИХ-системы. Бесконечную импульсную характеристику имеет рекурсивная ЛДС. ЛДС называется рекурсивной, если хотя бы один из коэффициентов a_j разностного уравнения:

не равен нулю. Порядок рекурсивной ЛДС определяется как max{N-1;M-1}.

Конечную импульсную характеристику имеет нерекурсивная ЛДС. Линейная ЛДС называется нерекурсивной, если все коэффициенты a_j равны нулю в уравнении:

Свойство памяти ЛДС-это свойство "помнить предысторию" - предшествующие отсчеты воздействия при вычислении реакции в текущий момент времени. Длительность предыстории (количество предшествующих отсчетов воздействия) определяет длительность памяти.

8.Передаточная функция. Карта нулей и полюсов . Критерий устойчивости лдс.

Передаточная функция — один из способов математического описания динамической системы. Используется в основном в теории управления, связи, цифровой обработке сигналов. Представляет собой дифференциальный оператор, выражающий связь между входом и выходом линейной стационарной системы. Зная входной сигнал системы и передаточную функцию, можно восстановить выходной сигнал. Для дискретных и дискретно-непрерывных систем вводится понятие дискретной передаточной функции. Пусть u(k) — входной дискретный сигнал такой системы, а y(k) -её дискретный выходной сигнал, k=1,2,… .(т.е. отношение Z-изображения реакции к Z-изображению воздействия при нулевых начальных условиях) Тогда передаточная функция W(z) такой системы записывается в виде:

здесь Y(z) и U(z)-это z преобразования для сигналов y(z) и u(z):

и ;

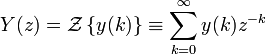Нулями называют значения Z, при которых передаточная функция равна нулю. Особыми точками (полюсами) называют значения Z, при которых знаменатель передаточной функции равен нулю. Карта нулей и полюсов – это совокупность нулей и полюсов на Z-плоскости. Звено называют базовым, если числитель его передаточной функции равен единице.

Устойчивость ЛДС. ЛДС называется устойчивой, если при ограниченном воздействии

max{x(n)} <= Rx, Rx != ∞, реакция будет также ограниченной.

max{y(n)} <= Ry, Ry !=∞.

Критерий устойчивости по ИХ: если ни один из коэффициентов разложения ИХ не равен нулю, то для того, чтобы ЛДС была устойчива, необходимо и достаточно, чтобы выполнялось условие абсолютной сходимости ряда : ;

Критерий устойчивости по передаточной функции: для того, чтобы ЛДС была устойчивой, необходимо и достаточно, чтобы все полюсы ее передаточной функции находились внутри круга единичного радиуса.