5. Определение дискретной системы. Виды дискретных систем.
Системой обработки сигналов называется объект, выполняющий требуемые преобразования входного сигнала в выходной. Входной сигнал называется воздействием, выходной - реакцией. Y=F{X}. X и Y - векторы, элементами которых являются воздействия и реакции, а F - оператор, определяющий математическое преобразование.
Система называется линейной, если:
F{x1+x2+x3+...} = F{x1}+F{x2}+F{x3}+...;
F{ax} = a*F{x}.
Соотношение вход-выход линейной системы описывается линейным уравнением. Система называется дискретной, если она преобразует входной дискретный сигнал в выходной дискретный сигнал. Дискретная система называется стационарной, если ее реакция инвариантна по отношению к началу отсчета времени. X(n-m) => y(n-m).
Начальные условия в дискретной системе могут быть нулевыми или ненулевыми.
Нулевые условия: x(n) = 0 => y(n) = 0.
Ненулевые условия: x(n) = 0 => y(n) != 0.
Дискретная система называется физически реализуемой, если для нее выполняются условия физической реализуемости (принцип причинности):
1) при нулевых начальных условиях реакция не может возникнуть раньше воздействия.
2) значения реакции в каждый момент времени зависят от текущего и предшествующих значений воздействия, но не зависят от его последующих значений).
6.Импульсная и переходная характеристики. Формула свертки.
Импульсная характеристика h(k) дискретной системы является откликом системы на единичную импульсную функцию x0(k), являющуюся аналогом дельта-функции при описании дискретных систем и представляющую собой единичный отсчет с единичным значением:
(1)
Импульсная характеристика показывает реакцию дискретной системы на подачу на ее вход единичной импульсной функции.
y0(k) = F(x0(k)) = h(k) (2)
Импульсная характеристика является основной характеристикой линейной системы: зная ее можно определить реакцию на любое воздействие.
Выведем формулу расчета отклика системы на произвольное воздействие x(k) через импульсную характеристику. Воздействие x(k) можно записать в виде линейной комбинации единичных отсчетов:
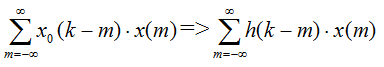
ЛДС
U1(k)
g(k)
g(k)
Формула свертки
Дискретная свертка позволяет описать взаимосвязь выхода дискретной системы с ее входом с помощью импульсной характеристики дискретной системы:
1)
2)
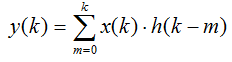
Свертка так же может быть записана в сокращенном виде:
y(k)=h(k)*x(k)
ЛДС, соотношение вход-выход которой описывается в виде формулы свертки, отвечает условиям физической реализуемости.
Линейные уравнения свертки решаются методом прямой подстановки при нулевых начальных условиях. Поэтому формула свертки непосредственно описывает алгоритм вычисления реакции по известному воздействию и ИХ ЛДС.
y(0)=x(0)*h(0)=2;
y(1)=x(0)*h(1)+x(1)h(0)=5;
y(2)=x(0)*h(2)+x(1)h(1)=6;
y(3)=4;
y(4)=x(1)*h(3)=1;
