3. Определение z-преобразования. Область сходимости. Соотношение между z и p-плоскостями.

Для анализа дискретных сигналов и линейных систем широко используется Z-преобразование, которое является обобщением дискретного преобразования Фурье. Z-преобразование позволяет ввести понятие передаточной функции и описать соотношение вход-выход в виде алгебраических уравнений.

Z-преобразование получается на основе дискретного преобразования Лапласа в результате замены (T – период дискрет-ции, ; оператор Лапласа). преобразование одностороннее, т.к. x(nT) определено только для n>=0 :

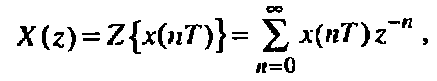
Комплексная переменная z может быть представлена в 2 формах: алгебраической и показательной.

– символическое обозначение Z-преобразования.

x(nT) – оригинал – вещественная или компл последовательность.

X(z) – z-изображение последовательности x(nT).

Z-преобразование однозначно связывает последовательность x(nT) с ее z-изображением X(z) и справедливо в области абсолютной сходимости ряда:

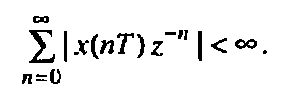
которую называют областью сходимости z-изображния. (сумма по членам преобразования является конечной). Область сходимости: |z|>R (в виде окружности с радиусом R на комплексной плоскости).

Связь между p- и z- плоскостями определяется соотношением:

=>

Выразив радиус r и угол :

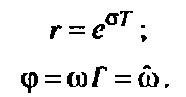
Видим, что угол есть нормативная частота в радианах.

4. Основные свойства z-преобразований. Способы вычисления прямого и обратного z-преобразований.

Основные свойства Z-преобразования:

0) Единственнось – последовательность x(nT) однозначно определяется z-изображением X(z) в области сходимости, верно и обратное.

1) Линейность. Z-образ суммы двух сигналов равен сумме z-образов этих сигналов.. Z{a₁x₁(n)+a₂x₂(n)+...} = a₁X₁(z)+a₂X₂(z)+...;

2) Теорема о задержке. Z{x(n-m)} = X(z)*z^-m; получили, что задержка исходного сигнала на m добавляет множитель Z^-m к z-преобразованию сигнала. Тогда задержка на один отсчет соответствует Z^-1.

3) Теорема о свертке. Пусть дано два сигнала x(nT) и y(nT), n=0..N-1. Найдем z-преобразование их круговой свертки. ;

т.о. z-изображние свертки = произведению z-изобр сверт-мых послед-тей.

Z-преобразование типовых дискретных сигналов:

1) Z-изображение единичного импульса Получаем

2) Z-изображение задержанного ед-го импульса

На основании т. задержки:

3) Z-изображение единичного скачка Получаем

4) Z-изображение задержанного ед-го скачка

5) Z-изображение последовательности.

На основе этих пунктов строится таблица соответствий которой можно пользоваться для вычислений различных z-изображений. Также можно использовать способ разложения z–изображения на простые дроби.

Обратное Z-преобразование определяется так:

Существует 3 классических способа найти обратное Z-преобразование:

- использование таблицы соответствий;

- прямое вычисление интеграла на основании теоремы Коши о вычетах;

- разложение Z-изображения на простые дроби.