44. Кодовая избыточность.

Предположим. Что дискретная случайная переменная r_k распределена в интервале [0, 1] и представляет значение яркости изображения.

P_r(r_k) - вероятность появления величины r_k.

P_r(r_k)=n_k/n

n – общее количество пикселей.

Если число битов используемых для представления каждого из значений r_k =L(r_k ), то среднее число битов требуемых для представления значения одного элемента равно:

L_ср= _k) P_r(r_k))

Присвоение кодовых слов (101) с меньшим числом битов более вероятностным значением яркости и наоборот более длинных кодовых слов менее вероятностным значением позволяет достичь сжатие данных, такой подход называется неравномерным кодированием.

Если значение яркости изображения получается некоторым способом, требующим большего числа символов, то изображение содержит кодовую избыточность.

45.Межэлементная(1) и визуальная (2) избыточности.

(1)Вычисляются коэффициент автокорреляция

y(Δn)=A(Δn)/A(0)

A(Δn)=1/N+Δn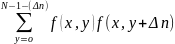

y y слабая корреляция

0 x 0,01 Δn

y сильная корреляция

2 1 Δn

Поскольку значения любого элемента изображения может быть достаточно точно предсказано по значениям его соседей, то информация содержащаяся в отдельном элементе оказывается относительно малой.

Для уменьшения избыточности в изображении двумерный массив пикселей должен быть преобразован в некоторый более рациональный вид (преобразование отображения).

Если из преобразованного набора данных может быть восстановлено исходное изображение считается обратным. Пример – ДПФ.

(2)Воспринимаемая глазом яркость зависит не только от количества света исходящего из просматриваемой области, но и от других факторов.

При обычном визуальном восприятии часть информации оказывается менее важной, чем другая такую информацию называют визуальная избыточность. Она может быть удалена без заметного ухудшения визуального качества изображения.

Важнейшей операцией, при оцифровки зрительной информации основанной на указанном, явлении квантования изображения.

46.Основные алгоритмы сжатия без потерь.

Алгоритмы сжатия без потерь обычно состоит из 2-х независимых операция:

1. Разработка альтернативного представления изображения, в котором уменьшена межэлементная избыточность.

2. Кодирование полученных результатов для устранения кодовой избыточности.

К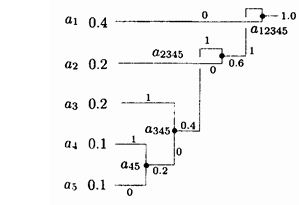 одирование Хафмана

При независимом кодировании сигналов источника изображения кода Хафмана обеспечивают наименьшее число кодовых символов (битов) на символ источника.

Код Хафмана является мгновенным однозначно декодированным блочным кодом.

Арифметическое кодирование

Выполним алгоритм для цепочки “aaba”:

Недостатки: необходимость включения некоторого символа окончания, позволяющего отделить одну кодовую комбинацию от другой. Исп-ние арифм-ки конечной точности.

LZW-кодирование. Не требует априорного знания вероятностей появления кодируемых символов.

Алгоритм:

При запуске процесса кодирования строится начало кодовой … (словарь), содержащей лишь кодируемые символы источника . Кодер последовательно анализирует символы источника и при появлении отсутствующей в словаре серии она помещается в определенную алгоритмом позицию словаря.

Пример: ававс

а000 в001 с010 ав011 ва100 авс101

Результат: 000 001 011 010

Кодирование битовых плоскостей

Основано на предварительном разложении интеграционного изображения на серию двоичных изображений и последующего кодирования каждого из них.

Одномерное кодирование длин серии

25 25 23 23 23

2 25 3 23