42. Геометрические преобразования.
• Две основные операции:
1. пространственное преобразование, в результате которого
происходит изменение расположения точек изображения
в плоскости;
2. интерполяция значений яркости, при которой
происходит присвоение значений яркости точкам
и
зображения,
подвергнутого пространственному
преобразованию.
Пространственные преобразования
– f(x,y) --> g(x’,y’)
• x’=r(x,y)
• y’=s(x,y)
– Алгоритм:
•
Ищем
(x0,y0) для f
•
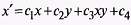Подставляем
(x0,y0), получаем (x0’,y0’)
• f (x0,y0)=g(x0’,y0’)
• Интерполяция значений яркости
– Пространственные преобразования могут давать не целые
значения (x', y').
– Возможные варианты реализации:
• По ближайшему соседу
• Билинейная
интерполяция
43. Сжатие изображений. Основные виды избыточности.
Сжатие данных (англ. data compression) — алгоритмическое преобразование данных, производимое с целью уменьшения их объёма. Сжатие основано на устранении избыточности, содержащейся в исходных данных. Простейшим примером избыточности является повторение фрагментов. Коэффициент сжатия
Коэффициент сжатия — основная характеристика алгоритма сжатия. Она определяется как отношение объёма исходных несжатых данных к объёму сжатых, то есть:
k = So/Sc, где k — коэффициент сжатия, So — объём исходных данных, а Sc — объём сжатых. Таким образом, чем выше коэффициент сжатия, тем алгоритм эффективнее. Следует отметить:
если k = 1, то алгоритм не производит сжатия, то есть выходное сообщение оказывается по объёму равным входному;
если k < 1, то алгоритм порождает сообщение большего размера, нежели несжатое, то есть, совершает «вредную» работу.
Ситуация с k < 1 вполне возможна при сжатии.
Различные алгоритмы могут требовать различного количества ресурсов вычислительной системы, на которых они реализованы:
- оперативной памяти (под промежуточные данные);
- постоянной памяти (под код программы и константы);
- процессорного времени.
Цифровые изображения, как и другие хранимые данные почти всегда обладают избыточностью. Для устранения межэлементной избыточности (коррелированности соседних пикселов) в методах сжатия изображений с потерями, как правило, применяются специальные преобразования, концентрирующие энергию в относительно небольшом количестве коэффициентов. К тому же особенности восприятия изображений человеческим глазом позволяют закодировать грубо значительную часть спектра без ущерба для воспринимаемого качества восстановленного изображения и таким образом устранить визуальную избыточность.
Пространственная. Она возникает тогда, когда рядом касаясь друг друга, расположены пикселы одного и того же тона, яркости и насыщенности.
Спектральная. Здесь избыточность связана с тем, что глаз человека больше чувствителен к яркости, чем к цвету пиксела. Поэтому в неярких местах искажение цвета не будет заметно.