39. Частотные фильтры.
Частотная область представляет собой ничто иное как пространство, в котором принимают значения переменные (u,v) фурье-преобразования.
Основы фильтрации в частотной области:
Процедура фильтрации состоит из следующих шагов:
Исходное изображение умножается на (-1)x+y, что бы его Фурье преобразование оказалось центрированное.
Вычисляется прямое ДПФ-изображение F(u,v).
Фурье функция умножается на функцию фильтра F(u,v) * H(u,v).
Вычисляется обратное ДПФ от результата шага 3.
Выделяется вещественная часть результата шага 4.
Результат шага 5 умножается на (-1)x+y.
Причина по которой множитель H(u,v) называется фильтром (передаточная фун-я фильтра) состоит в том, что он подавляет некоторые частоты преобразования, оставляя при этом другие без изменения.
Пусть f(x,y) обозначает вх. изображение после шага 1, и пусть F(u,v) есть его фурье-образ. Тогда Фурье-образ выходного изображения определяется выражением
Умножение функций двух переменных H и F осуществляется поэлементно.
Фильтрованное изображение получается вычислением обратного преобразования Фурье от фурье-образа G(u,v):
Искомое
изображение получается выделением
действительной части и умножения на
(-1)x+y
,чтобы
скомпенсировать эффект от умножения
вх. изобр. на ту же величину.процедура
фильтрации схематич. отображена на
рис. в неск. более общем виде.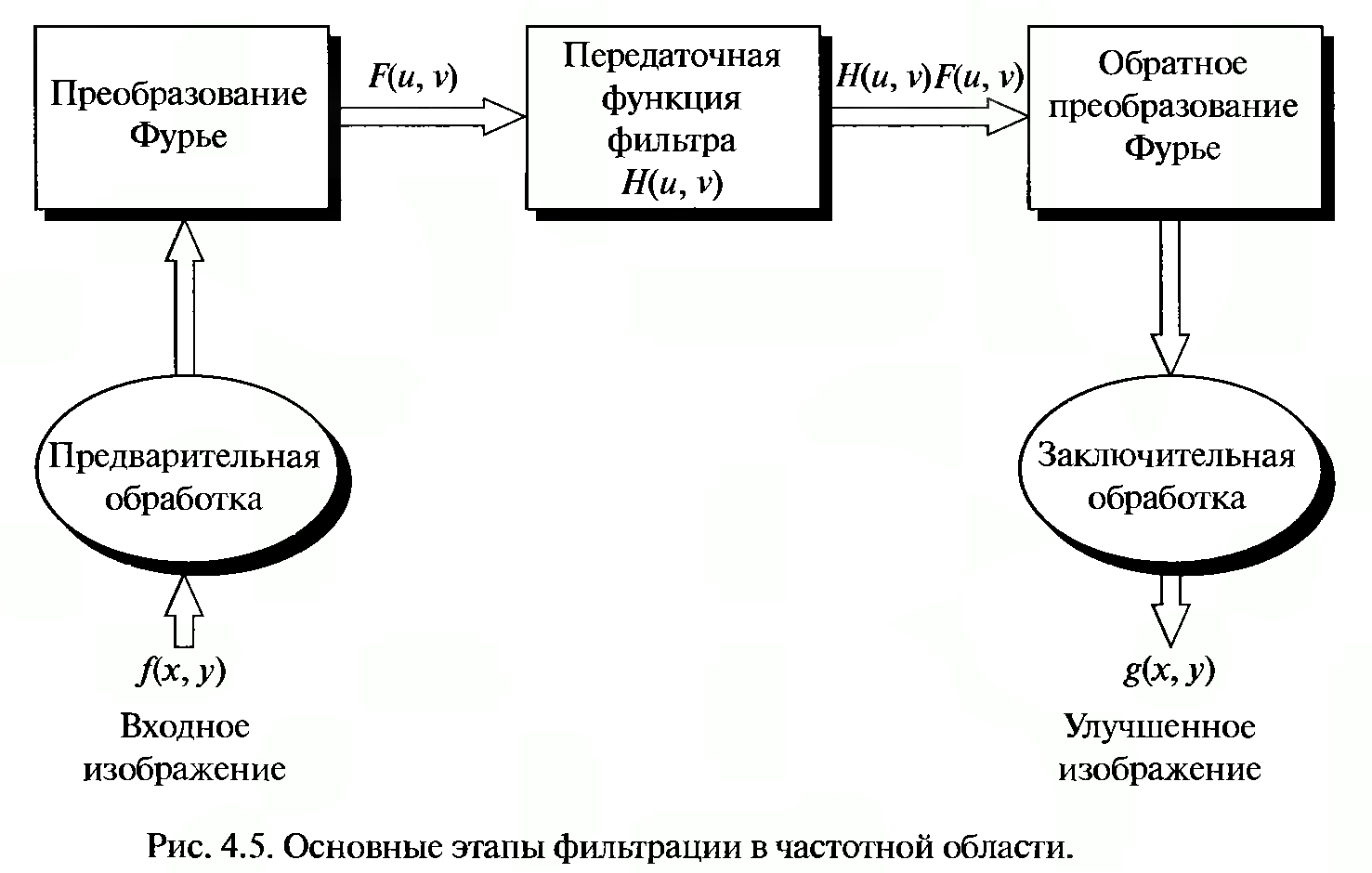
40. Оценки искажающей функции.
Оценка искажающей функции необходима для получения параметров искажения, которые будут использоваться для дальнейшей коррекции изображения.
Визуальный анализ. Пусть рассматриваемая часть изображения (сигнал с большей амплитудой) – gs(x,y), а построенное не размытое изображение на основе яркостей объекта и фона (приближение для части неискаженного изображения в рассматриваемой области) –
(x,y).
И пусть действие шума пренебрежительно
мало, тогда действие отражающего
оператора:
Эксперимент. Оценка на основе эксперимента:
- подбираем параметры системы для воспроизведения изображения
- также нужно сформировать импульсный отклик.
Тогда
,
где
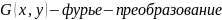полученного изображения, а A
– константа, описывающая величину
яркости импульса.
Моделирование. Моделируются различные искажения изображения. Примеры:
- турбулентность атмосферы. Подставляя различные коэффициент k, создаем модели изображения с соответствующим искажением.
- равномерное движение сцены в кадре.
* x0(t) и y0(t) описывают закон движения в направлении x и y.
* T – время экспозиции
* g(x,y) – смазанное изображение
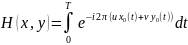
41. Инверсная и Винеровская фильтрация.
Инверсная фильтрация.
Простейшим способом восстановления четкости изображения является обработка наблюдаемого изображения в пространственно-частотной области инверсным фильтром [4.5]. Передаточная функция инверсного восстанавливающего фильтра определяется соотношением
Она
выбирается из условия
, обеспечивающего компенсацию искажений,
вносимых ФРТ формирующей системы.
Восстановленное изображение равно сумме исходного изображения и шума наблюдения, прошедшего через инверсный фильтр. При отсутствии шума достигается точное восстановление инверсным фильтром исходного изображения по искаженному изображению.
Если же объекты не наблюдаются на фоне постоянной яркости и не расположены в центре кадра, то восстановить изображение инверсным фильтром не удастся из-за краевых эффектов.
Существуют частные методы ослабления шумов, которые заключаются в ограничении полосы инверсного фильтра. Однако эти методы не решают проблем краевых эффектов и наличия нулей передаточной функции формирующей системы в рабочем диапазоне частот.
Таким образом, несмотря на очевидную простоту метода инверсной фильтрации, он может успешно использоваться для восстановления ограниченного класса изображений, у которых уровень фона на краях постоянен. Кроме того, метод инверсной фильтрации обладает чрезвычайно низкой помехоустойчивостью.
Винеровская фильтрация.
• Учитывает искажающую функцию и статистические
свойства шума
• Минимизирует среднеквадратичное отклонение:
–
Найти
такое
,
чтобы
было
минимальным (E-мат.ожидание, f – неискаженное изобр.)
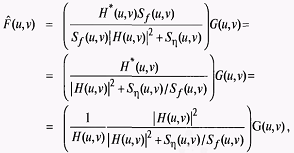
Если спектры неизвестны:
