2. Фильтры порядковых статистиках

Виды:

*медианные фильтры

Действие этого фильтра, как следует из его названия, состоит в замене значения в точке изображения на медиану значений яркости в окрестности этой точки:

Широкая популярность медианных фильтров обусловлена тем, что они прекрасно приспособлены для подавления некоторых видов случайных шумов, и при этом приводят к меньшему размыванию по сравнению с линейными сглаживающими фильтрами того размера.

*фильтры, основанные на выборе максимального и минимального значения

Например, использование 100-го процентиля приводит к фильтру, основанного на выборе максимального знач.(или фильтру максимума)который задаётся выражением

Такой фильтр полезен при обнаружении наиболее ярких точек на изображении.

А при использовании 0-го процентиля приводит к фильтру, основанного на выборе минимального значения( или фильтру минимума), который полезен при обнаружении наиболее тёмных точек на изображении.

*фильтр серединной точки

Заключается просто в вычислении среднего между максим. и миним. значением

Этот фильтр объединяет в себе методы порядковых статистик и усреднения. Этот фильтр лучше всего работает при наличии случайно распределённых шумов, как гауссов или равномерный.

38. Адаптивные фильтры подавления шума.

Изменяются в зависимости от статистических свойств изображения внутри области действия фильтра.

* Адаптивные локальные фильтры подавления шума

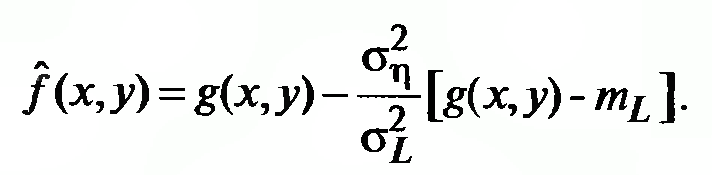
Определяется следующими условиями:

- если дисперсия шума равна 0. То отклик фильтра равен g(x, y).

- если локальная дисперсия на много больше дисперсии шума, то значение отклика фильтра должно быть больше яркости этих точек.

- если обе дисперсии принимают значения второго порядка, то отклик фильтра должен быть равен локальной средней по области.

*Адаптивные медиальные фильтры

Эти фильтры помогают справиться с импульсным шумом, вероятности которого превышают указанные значения. Дополнительное преимущество адаптивного медиального фильтра состоит в том, что такой фильтр “старается сохр. детали” в областях, искажённых не импульсным шумом.

Введём следующие понятия:

Z_min – минимальное значение яркости

Z_max – максимальное значение яркости

Z_med – медиана значений яркости в

z_xy – значение яркости в теневой точке

S_max – максимальный размер области

Алгоритм фильтрации состоит из двух ветвей, обозначенных ниже как ветвь А и B:

Ветвь А: A₁=z_med-Z_min

A₂=z_med-Z_max

Если А₁>0 и А₂<0, то перейти к ветви В, иначе увеличить размер окрестности.

Если размер окрестности ≤ S_max, повторить ветвь А, иначе результат равен z_xy

Ветвь В: В₁= -z_min

B₂=z_xy-z_max

Если В₁>0 и В₂<0, результат равен z_xy, иначе результат равен z_med.

Применяются для удаления биполярного импульсного шума, сглаживание шума в других типах. Сведения к минимуму таких искажений, как чрезмерное уточнение или границ объектов.