34. Сглаживающие частотные фильтры.

Контуры и другие резкие перепады яркости на изображении вносят значительный вклад в высокочастотную часть Фурье-перобразования. Цель состоит в выборе передаточной функции, которая ослабит высокочастотные компоненты и сформирует сложное изображение.

Существует 3 типа фильтров:

- Идеальные фильтры низких частот

Недостатки: его можно реализовать только программным способом, на изображении возникает эффект звона (появление лже-контуров).

- Фильтр нижних частот Баттерворта

n – порядок фильтра.

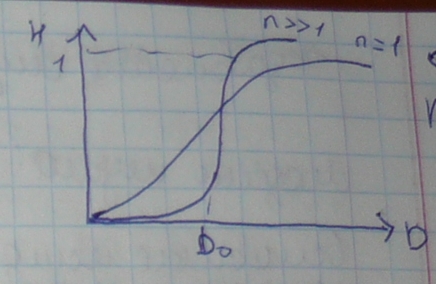
При использовании фильтра Баттерворта порядка 1 звон не возникает. Но может стать значительным при использовании фильтров более высокого порядка.

- Гаусовые фильтры низких частот

Достоинства: отсутствует эффект звона.

36. Частотные фильтры повышения резкости

Поскольку контуры и другие скачкообразные изменения яркости связаны с высокочастотными составляющими, то повышение резкости изображения может быть достигнуто частотной областью при помощи процедуры высокочастотной фильтрации.

H_вч(u, v) = 1-H_нч(u, v)

Рассмотрим идеальные высокочастотные фильтры, высокочастотные фильтры Баттерворта и гауссовы высокочастотные фильтры:

- идеальные фильтры высоких частот

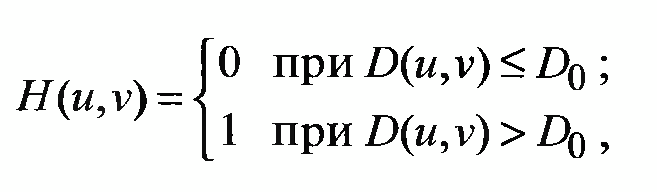
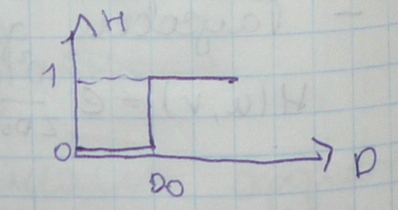
- фильтры высоких частот Баттерворта

- Гауссовы фильтр высоких частот

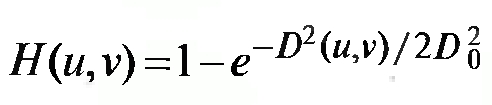
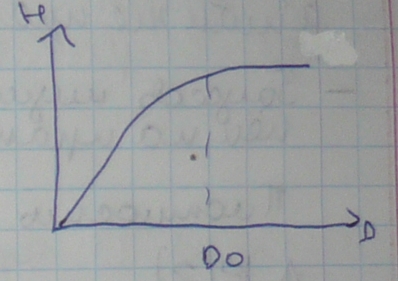
Гуассов фильтр даёт хорошее качество фильтрации даже для маленьких объектов и тонких полос.

37. Пространственные фильтры подавления шума.

Когда искажение изображения обусловлено исключительно наличием шума, равенства приобретает вид

g(x, y)=f(x, y)+ȵ(x, y)

G(u, v)=F(u, v)+N(u, v)

1. Усредняющие фильтры

Здесь мы кратко обсудим пространственные фильтры для подавления шума и построим некоторые др. фильтры, эффективность которых лучше.

-Фильтр, основанный на вычислении среднего арифметического

Такой фильтр, наз. среднеарифметическим, яв-ся простейшим среди усредняющих фильтров.

Пусть обозначает прямоуг. окрестность (множ. координат точек изобр.) размерами m*n c центром в точке (x,y). Процедура фильтрации предполагает вычисление ср. арифм. значения

искажённого изобр. g(x,y) по окрестности

Усредняющий фильтр просто сглаживает локальные вариации яркости на изображении. Уменьшение шума происходит в результате этого сглаживания.

-Фильтр, основанный на вычислении среднего геометрического

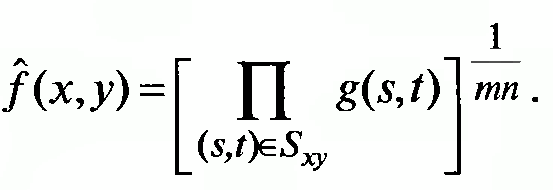Здесь значение восстановленного изображения в каждой точке (x,y) яв-ся корнем степени mn из произведения значений в точках окрестности

- Фильтр, основанный на вычислении среднего гармонического

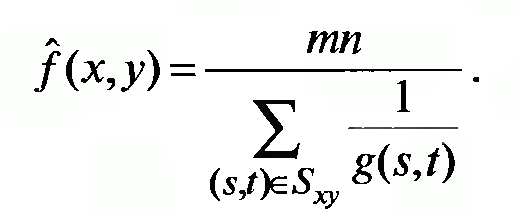Среднегармонический фильтр хорошо работает в случае униполярного “белого” импульсного шума (т.е. когда значение шума соответствует появлению белых точек на изображении), но не работает в случае униполярного “чёрного импульсного шума”. Этот фильтр также хорошо работает для др. типов шума, таких как гауссов шум.

- Фильтр, основанный на вычислении контрагармонического

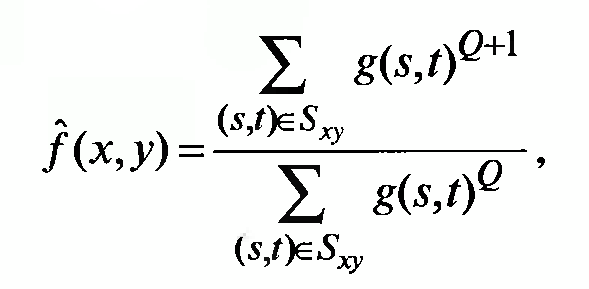где Q называется порядком фильтра . Этот фильтр хорошо приспособлен для уменьшения или почти полного устранения импульсного шума. При полож. значениях Q фильтр устраняет “чёрную” часть импульсного шума. При отриц-х значениях Q фильтр устраняет “белую” часть импульсного шума. Обе части шума не могут быть устранены одновременно.